Que representa la gardenia
La belleza de un set de perfume, que representa la gardenia, gardenia o bien gardenia comestible, es que te deja probarte varias versiones de ti misma o sumergirte absolutamente en una identidad a través del agua de baño, los jabones y las lociones corporales. Pues algunos días eres una frágil flor y otros eres cálida y sensual con un espíritu picante. Pocos regalos para los hombre o bien mujeres, así sea para ti o para alguien cercano a ti, tienen la magia de evocar recuerdos del mismo modo en que el aroma toca un acorde personal. Reduzca las opciones desde lo dulce y afrutado hasta lo terrenal y almizclado con nuestra guía de los mejores perfumes para ella. Para comprender mejor lo que quieres en una fragancia, piensa en las que has utilizado anteriormente, o en las que has sentido que te agradan (así sea que tus amigos, colegas o bien familiares utilicen fragancias que han dejado impresiones positivas). Mira las familias de fragancias a las que pertenecen estos olores, o bien sus notas.
Listado top ventas para Que representa la gardenia
Con esta de productos vamos a mostrarte lo mejor en que representa la gardenia para el confort de tu cuerpo. Toma conocimiento de que para encontrar un montón de opciones para obtener lo mejor para tu bienestar, te encuentras en uno de los mejores sitios web de la red.

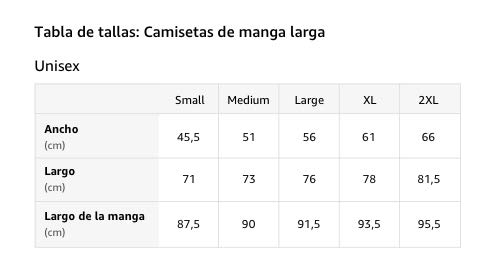
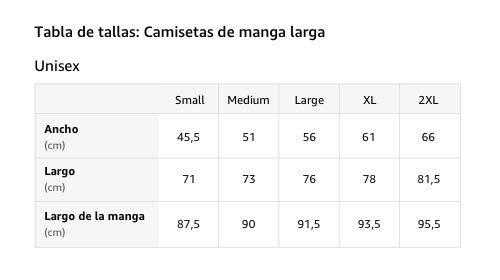
Gardena California CA - Diseño deportivo vintage, color rosa Manga Larga
- ¿Buscas una camisa para representar a Gardena California? Ya sea para un evento deportivo como softball, fútbol, béisbol, baloncesto o tal vez simplemente te guste Gardena CA, este diseño deportivo deportivo es perfecto para cualquier ocasión.
- Esta letra de bloque vintage de Gardena CA College College en color rosa y diseño de contorno blanco con un aspecto retro ligeramente desgastado y envejecido hace que sea una idea de regalo perfecta como recuerdo de viaje o camisa de ciudad natal.
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


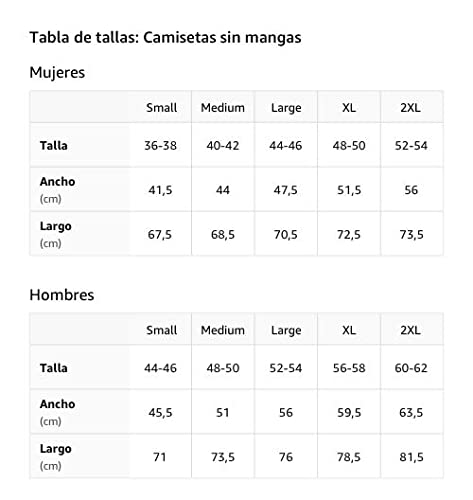
Gardena California CA - Diseño deportivo vintage Camiseta sin Mangas
- ¿Buscas una camiseta para representar a Gardena California? Ya sea para un evento deportivo como softball, fútbol, béisbol, baloncesto o tal vez te guste Gardena CA, este diseño deportivo es perfecto para cualquier ocasión.
- Esta letra de bloque vintage de Gardena CA College University en color azul marino y diseño de contorno blanco con un aspecto retro ligeramente desgastado y envejecido hace que sea una idea de regalo perfecta de viaje o camisa de ciudad natal.
- Ligero, Encaje clasico, manga de doble puntada y bastilla baja


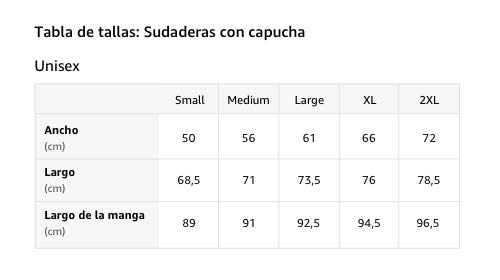
Gardena California CA - Diseño deportivo vintage Sudadera con Capucha
- ¿Buscas una camiseta para representar a Gardena California? Ya sea para un evento deportivo como softball, fútbol, béisbol, baloncesto o tal vez te guste Gardena CA, este diseño deportivo es perfecto para cualquier ocasión.
- Esta letra de bloque vintage de Gardena CA College University en color azul marino y diseño de contorno blanco con un aspecto retro ligeramente desgastado y envejecido hace que sea una idea de regalo perfecta de viaje o camisa de ciudad natal.
- 241 gr, Encaje clasico, Cinta de sarga en el cuello


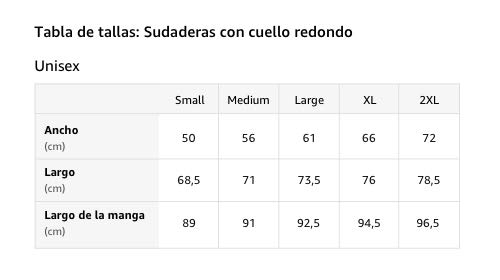
Gardena California CA - Diseño deportivo vintage Sudadera
- ¿Buscas una camiseta para representar a Gardena California? Ya sea para un evento deportivo como softball, fútbol, béisbol, baloncesto o tal vez te guste Gardena CA, este diseño deportivo es perfecto para cualquier ocasión.
- Esta letra de bloque vintage de Gardena CA College University en color azul marino y diseño de contorno blanco con un aspecto retro ligeramente desgastado y envejecido hace que sea una idea de regalo perfecta de viaje o camisa de ciudad natal.
- 241 gr, Encaje clasico, Cinta de sarga en el cuello


Gardena California CA - Diseño deportivo vintage Manga Larga
- ¿Buscas una camiseta para representar a Gardena California? Ya sea para un evento deportivo como softball, fútbol, béisbol, baloncesto o tal vez te guste Gardena CA, este diseño deportivo es perfecto para cualquier ocasión.
- Esta letra de bloque vintage de Gardena CA College University en color azul marino y diseño de contorno blanco con un aspecto retro ligeramente desgastado y envejecido hace que sea una idea de regalo perfecta de viaje o camisa de ciudad natal.
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Ravensburger-15175 My Haven No. 6. The Cosy Shed - Rompecabezas de 1000 Piezas para Adultos y niños a Partir de 12 años, Multicolor (15175)
- N.º 6 en la colección "My Haven" de rompecabezas para adultos, que representa paraísos, santuarios y retiros para relajarse. El acogedor cobertizo representa al propietario leyendo un libro frente a un quemador de madera calentito
- La marca de rompecabezas más vendida en todo el mundo: con más de mil millones de rompecabezas vendidos, nuestros rompecabezas son regalos ideales para mujeres, grandes regalos para hombres y encajan perfectamente en nuestro tablero de rompecabezas
- Nuestras sierras de calar de 1000 piezas están fabricadas con calidad premium y miden 70 x 50 cm cuando están completas. Ideal para adultos y rompecabezas ideales para niños de 12 años en adelante.
- Nuestros rompecabezas utilizan un cartón exclusivo y extra grueso combinado con nuestro fino papel estructurado de lino para crear una imagen de rompecabezas sin reflejos y darte la mejor experiencia posible.
- Rompecabezas positivo: desde divertidos momentos familiares juntos hasta beneficios para la salud a largo plazo y momentos conscientes del día a día, hay tantos positivos sobre el humilde rompecabezas Son un gran regalo de cumpleaños o regalo de Navidad


Jembrana Incense - Conos de Incienso Jembrana: Mezcla 6 Aromas (60 Conos en Total), 10 Conos de Loto (Padma), sándalo, Gardenia, Maha Triloka, Raja Harum y Dewi Sai (ámbar), Juegos de Regalo
- Conos de incienso de 1.6 pulgadas con un tiempo de combustión de aproximadamente 35 minutos y aromas fragantes de larga duración de flores tropicales, madera, hierbas y especias, que son representativos de los aromas de la isla de los dioses Bali. El cono de incienso es firme, se tarda un poco más en encender el incienso al inicio del encendido. Intente encender la varilla de incienso dentro de 1 centímetro.
- Hecho a mano de forma natural y tradicional en Bali por los balineses locales
- Su compañero perfecto para la relajación, la meditación, el yoga, la aromaterapia, la curación y para crear una atmósfera de buen karma integral
- Una idea de regalo de Navidad pensada y sabrosa para familias y seres queridos.
- GARANTÍA DE SATISFACCIÓN DEL 100%: todos tienen sus propios gustos, sentidos y preferencias personales, y eso está bien. Entonces, si por alguna razón no está satisfecho con nuestros productos, no dude en devolverlos para obtener un reembolso completo.


Piy Painting Cuadro en Lienzo de Flor de Gardenia Murales Decoración Impresiones de Lienzo Imagen de Florero Abstracto para Hogar Pintura Listo para Colgar Aniversario 3X 30x30cm
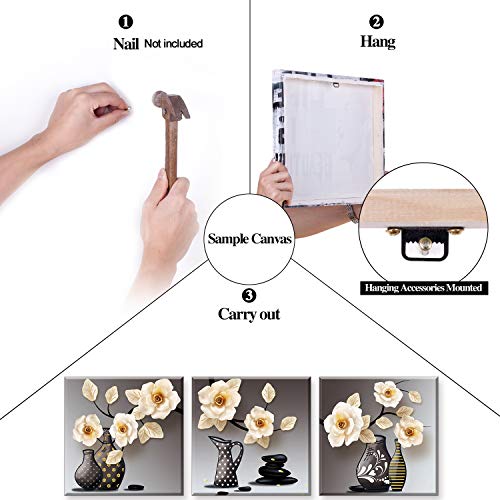
- 1: Alta calidad Impresión de sobre lienzo de Giclee en PIY PAINTING. Elija una decoración de pared que sus familiares y amigos admirarán durante muchos años. Dimensión: 3picsx30x30cm. La flor de gardenia representa el amor eterno, el amor puro e impecable. Representando la esperanza interior. Un espíritu de lucha constante hacia tus objetivos.
- 2: Tabla de Arte Claro y Seguridad. Nuestro lienzo enmarcado con cuidado y listo para colgar, es impermeable y bien para el baño. Nuestra pintura es ideal para cualquier habitación de su apartamento que le gustaría iluminar: salas de estar, oficinas o salas de espera, sala de estar o dormitorio.
- 3: Giclée de alta definición, ilustración moderna sobre lienzo, impresión fotográfica de lienzo de alta calidad. Imagen clara de color puro. Añade viabilidad y estética a tu hogar.
- 4: Buena elección como regalo para hombres importantes. Es una bonita decoración de pared para la sala de estar, el dormitorio, la cocina, la oficina, el hotel, el comedor, la oficina, el bar, etc. Haz tu habitación más encantadora.
- 5: Calidad y servicios garantizados. Sin problemas de postventa, si necesita servicio, estamos siempre a su lado.


GARDENIX 2.5 m madera Cercado para Bancal Césped Jardín Palisade Valla Terracotta
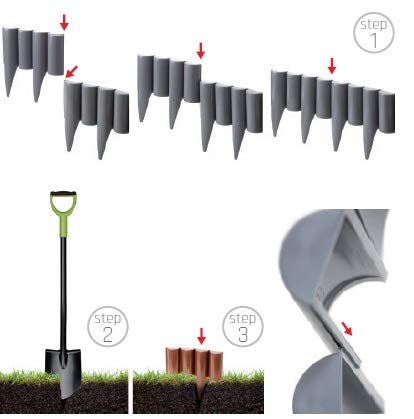
- Con el borde para césped se puede delimitar rápida y fácilmente el césped o arriates. Debido a las conexiones flexibles, las esquinas y las curvas no son un problema.
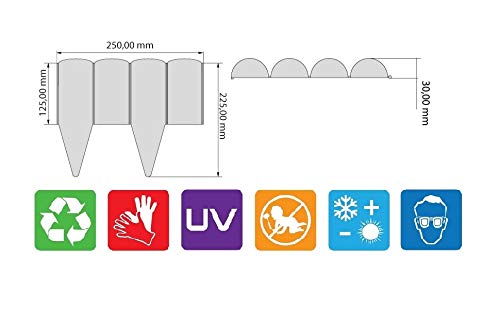
- El empalizado está hecho de un plástico elástico y resistente a la intemperie. El empalizado es flexible y se puede colocar en posición recta, curvada o circular. Gracias al enrejado de 125 mm de alto, la madera imita se puede organizar con buen gusto tanto un jardín pequeño como un grande. El empalizado está disponible en varios colores, por lo que el color de la palisada se puede adaptar fácilmente al entorno, como la fachada de la casa, la valla o los muebles de jardín.
- Un artículo contiene 10 módulos, que se pueden montar en una valla de 2,5 m de longitud (posibilidad de ampliación infinita)
- Tamaño – un elemento (L x H): 25 cm x 22,5 cm
- El empalizado representa un compromiso entre diseño interesante, buena calidad y bajo precio. Debido a su buena presencia, este empalizado se distingue de otros palisados de plástico y se presenta muy bien con piedras naturales y plantas


Opinel 1617 Navaja, multicolor
- Artesanía suiza.


BlueXP 2 Pieza180cm Guirnalda de Flores Artificial Flor Seda Artificiales Colgante Vines Guirnaldas de Hermoso Flores de Cerezo para Familiar la Fiesta Jardín Navidad Decoración Champagne
- 2 Pezzia vides de cerezo artificiales de 180 cm, 260 flores/vides, 4 flores de cerezo de 5.6 cm de diámetro florecen en un solo lugar, las flores son realistas, naturales y verticales, y el efecto colgante es mejor.
- Las flores de cerezo están hechas de flores de seda de alta calidad, la enredadera es de plástico flexible, flores se pueden quitar y poner de nuevo por un diseño de hebilla, tiene agujero de alambre verde en ambos extremos que viene en práctico para colgar, para uso interior y exterior.
- Flor de cerezo es un símbolo de vida y felicidad, representa un espíritu cálido, puro y noble, ella es muy adecuada para la decoración de la boda, dando una sensación romántica e inolvidable.
- Puedes colgar en la pared, puerta, columpio, espejo y en cualquier lugar, porque te gusta disfrutar de las hojas artificiales con vides.
- Sakura vine es adecuado para: decoración de parques, arcos, techos de centros comerciales, decoración de hoteles para bodas, decoración de bodas, hoteles, discotecas, parques, etc.


Ferrari & Arrighetti Figura de la Sagrada Familia en Talla de Madera Encerada para Nacimiento de 8 cm - Colección Belén Demetz Deur
- Esta pieza representa a la Virgen María, el Niño Jesús y San José; todos ellos sobre la misma base
- Son las figuras principales del Belén y en torno a ellos se dispone el resto de personajes
- La altura de 8 cm hace referencia a San José, el resto de figuras están diseñadas en proporción
- Se trata de una talla en madera, lijada y tratada con ceras de diferentes tonos (gama de marrones)
- Hecho en el Valle de Gardena, que cuenta con una larga tradición en el arte de la talla de madera


Ferrari & Arrighetti Imagen de San Antonio de Padua en Talla de Madera con Acabado Natural Que Mide 15 cm - Demetz Deur
- Se trata de una imagen tallada en madera, lijada, pero sin tratamiento de color
- San Antonio de Padua fue un sacerdote de la Orden Franciscana, predicador y teólogo portugués
- La iconografía cristiana suele representarlo con: la biblia, las azucenas y el Niño Jesús en brazos
- Hecho en el Valle de Gardena, que cuenta con una larga tradición en el arte de la talla de madera
- En este valle de los Alpes italianos, Oswald Demetz fundó la empresa "DEUR" en el año 1966


World's Okayest Market Gardener impreso mochila azul para niños, lindas mochilas, lindas mochilas pequeñas, lindas mochila negra, mochila negra fresca mochila de moda, mochilas grandes de moda, negro
- Adecuado para cualquier ocasión, como un viaje al aire libre, ir al zoológico, jugar en el parque o cualquier otra actividad al aire libre.
- Correas de hombro acolchadas ajustables, parte trasera y delantera acolchadas para protección y comodidad.
- Esta mochila de alta calidad es el accesorio perfecto para estudiantes de escuela.
- Esto representa un regalo asequible y práctico que podrán apreciar durante años.
- Gran rompehielos vendemos productos que son excelentes rompehielos, calentadores de corazón e inspiradores. ¡Productos que dicen algo!


Ferrari & Arrighetti Imagen de San Sebastián mártir en Talla de Madera Pintada a Mano Que Mide 15 cm - Demetz Deur
- La imagen ha sido tallada en madera, lijada, pintada a mano y embellecida con pan de oro
- San Sebastián fue un soldado del ejército romano, venerado como santo y mártir por la Iglesia
- Es posiblemente uno de los santos más representados y siempre aparece haciendo alusión a su martirio
- Su festividad se celebra el 20 de enero
- Hecho en el Valle de Gardena, que cuenta con una larga tradición en el arte de la talla de madera

Imágenes de Que representa la gardenia
Si para ti es más cómodo elegir de forma visual los productos, puedes ver aquí una agrupación de fotos de que representa la gardenia. Pincha una de las fotos y entrarás a la adquisición online de colonia en concreto viendo sus funcionalidades y precio.