Distribucion de perfumes
Así sea que esté en una tienda para una nueva fragancia de firma o bien esté buscando edificar su muestrario de fragancias, vea nuestra selección de los mejores perfumes para hombres y mujeres como distribucion de perfumes, distribucion de perfumes originales o bien equivalencias perfumes la botica de los perfumes. Es importante no utilizar perfume o bien productos corporales perfumados cuando se compra una nueva olor, en tanto que esto puede alterar el desarrollo de la fragancia escogida. Últimamente, ha habido un cambio gradual en la colonia, que se ha alejado de los olores de la tradición, como el almizcle, el tabaco y el licor negro, y ha pasado a un territorio más claro y botánico. Las notas cítricas, florales y amaderadas siempre han tenido una presencia sutil en la perfumería, mas se están volviendo poco a poco más prominentes debido al impulso cara las olores unisex.
Listado top ventas para Distribucion de perfumes
En este listado puedes comprar multitud de productos como distribucion de perfumes estupendos para el cuidado de tu bienestar. Nos queremos comprometer a que podrás encontrar las mejores opciones y precios de la totalidad de lo que necesites para tu bienestar, dándote la oportunidad de descubrir varias modelos y marcas.

SO SLIME- SLIMEGLAM (CANAL TOYS ESPAÑA DISTRIBUCION SL SSC111)
- Hazte tu propio slime con aroma mezclando los polvos con agua
- Añadele decoraciones
- Llevalo a donde quieras con este increible maletin
- Producto de calidad


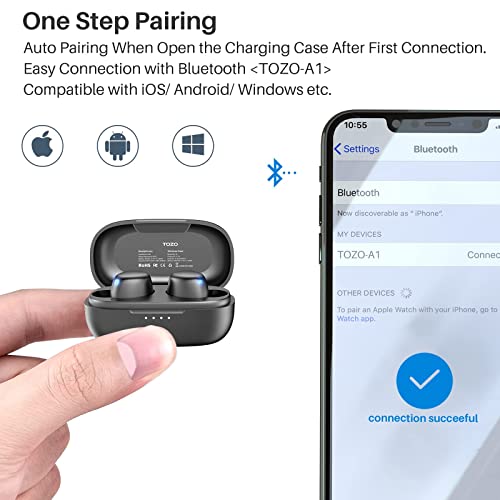
TOZO A1 Mini Auriculares inalámbricos Bluetooth 5.0 en la Oreja Auriculares livianos Micrófono Incorporado, Auriculares con Sonido Premium inmersivo (Compatible para Orejas pequeñas), Negro
- [Ultraligero y compacto] La superficie y el ángulo de la parte interna de los auriculares A1 se han pulido y refinado repetidamente para lograr un equilibrio entre belleza y comodidad y que sea cómodo de usar. Asimismo, un solo auricular pesa solo 3,7 g, haciéndolo tan ligero como una pluma y discreto al oído. El diseño ergonómico proporciona un ajuste cómodo y seguro que no sobresale de las orejas.
- [Calidad de sonido estéreo] El altavoz de 6 mm de diámetro de los auriculares TOZO A1 presenta un rango de sonido potente y amplio, que hace que los agudos estén llenos de dinámica y los graves potentes. agradable, apto para deportes o trabajo a domicilio
- [Control táctil inteligente] Los audífonos A1 admiten el control táctil de doble oído, lo que brinda una operación conveniente en el control de volumen, canción anterior / siguiente, pausa y respuesta a llamadas, así como control de asistente de voz.
- [Bluetooth 5.0 y conexión de larga distancia]] Con la tecnología Bluetooth 5.0, A1 tiene una calidad de sonido superior y una señal fuerte, por lo que no hay desconexión al escuchar música o hacer llamadas telefónicas dentro de los 12 metros.
- [Larga duración] Con auriculares de 40 mAh de capacidad y carga de 400 mAh de capacidad, los auriculares duran 6 horas para uso normal (60% de volumen), y el recipiente de carga dura 32 horas para 3 cargas, lo que le brinda una excelente experiencia de larga duración.


MAYJAM Aceites Esenciales de Jazmín 100 ml, 100% Aceites Esenciales Naturales Puros, Aceite Esencial de Aromaterapia de Grado Terapéutico, Aceites de Fragancia para Difusor Humidificador Relajación
- 💝Oferta Exclusiva de Febrero💝【LA MÁS ALTA CALIDAD GARANTIZADA, EL ACEITE DE JAZMíN MÁS Fresco】 - Lo que distingue a los Aceites Esenciales MAYJAM es su pureza y concentración incomparables. Naturales, sin adulterantes ni diluciones, sus aceites aportan el máximo beneficio posible y son intransigentes.
- ❤【NO SEA VÍCTIMA PARA OBTENER ACEITE DILUIDO DE JAZMíN BARATO】 - La mayoría de la competencia diluye su aceite con un aceite portador barato o incluso con otros productos químicos potencialmente peligrosos. Nuestro aceite de menta se prueba de forma rutinaria para determinar su pureza y otras cualidades únicas para garantizar que está comprando el aceite más puro disponible.
- ❤【BOTELLAS DE ALTA CALIDAD】- Utilizamos botellas de alta calidad con un revestimiento de color uv para proteger los aceites esenciales contra la luz solar y la degradación.
- ❤【PERFECTO PARA SU DIFUSOR, ACEITES CORPORALES Y MÁS】 - Simplemente agregue unas gotas a su difusor favorito, o haga un limpiador totalmente natural. ¡También es ideal para hacer lociones, cremas, bombas de baño, exfoliantes, velas y mucho más!
- ❤【MAYJAM PROPORCIONA LOS ACEITES ESENCIALES DE LA MÁS ALTA CALIDAD】 - Si no está 100% satisfecho con nuestros aceites, simplemente contáctenos para un reembolso completo o reemplazo.


Science4you - Super Laboratorio de Perfumes para Niños +8 Años - Kit Cientifico con 13 Experimentos para Niños: CREA Tus Perfumes y Sales de Baño, Laboratorio de Quimica, Juegos Educativos +8 Años
- 【 Super Laboratorio de Perfumes para Niños de +8 Años】Utilice los 63 contenidos incluidos en este kit de perfumes y aprenda a crear tus proprios perfumes con diferentes aromas. Explore los 13 experimentos científicos para niños en el laboratorio de ciencias y quimica para niños y diviértase hacendo increíbles perfumes caseros.
- 【 Experimentos Científicos para Niños 】Crea regalos increíbles y únicos para tus amigos con este kit de perfume casero. Combine los diferentes reactivos y aprenda a hacer diferentes perfumes con aromas fragancias increíbles.
- 【Libro Educativo en 7 Idiomas 】Este Kit Científico para hacer perfumes incluye un libro educativo incluido en 7 idiomas (inglés, alemán, francés, holandés, italiano, español, portugués) para guiarte por los diferentes experimentos deste laboratorio de ciencia y quimica.
- 【 Juegos Educativos para Niños +8 Años 】Este laboratorio de ciencias es perfecto para niños y niñas de 8 a 14 años que disfrutan del mundo de la ciencia y la cosmética. Un juguete educativo inspirado en la metodología STEAM (antes llamado juguetes STEM). STEAM significa Ciencia, Tecnología, Ingeniería, Artes y Matemáticas. Estos juegos de ciencia ayudan a los niños a adquirir conocimientos en estas 5 áreas, mejorando sus habilidades mientras juegan.
- 【 Regalo Original para Niños 】Este juguete científico para hacer perfumes es el regalo perfecto de Navidad o cumpleaños para niños. Un juguete hecho por científicos, en el que los padres confían y los niños lo adoran.


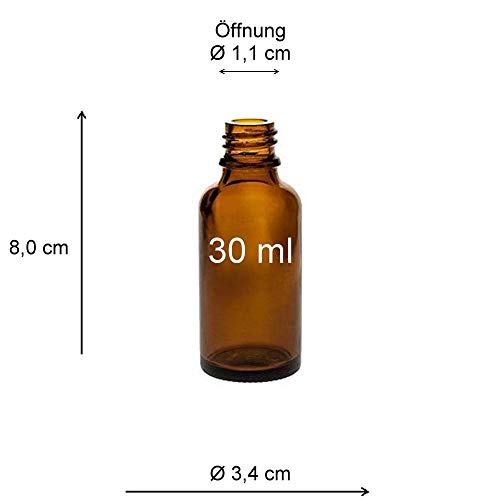
Viva-Haushaltswaren – 10 frascos cuentagotas de Vidrio, para Farmacia, Color marrón, Vidrio, marrón, 30 ml
- 10 botellas de vidrio de farmacia en color marrón cristal para fotosensible líquidos – Incluye pipetas de cristal/DIN 18
- Dimensiones: Altura: 8,0 cm sin pipeta y 10,4 cm con pipeta/Ø 3,4 cm/Ø Apertura 1,1 cm
- Capacidad: 30 ml (hasta el borde superior medido aprox.)
- Adecuado para: Flores de Bach, esencias, aceites, extractos, perfume, plata coloidal, etc. – Otros Descripción del producto S. abajo
- Contenido: 10 farmacia de botellas de vidrio, 10 pipetas de cristal, un embudo aprox 5 cm de diámetro

ACOFARMA F50+ maquillaje compacto
- De la marca Acoderm


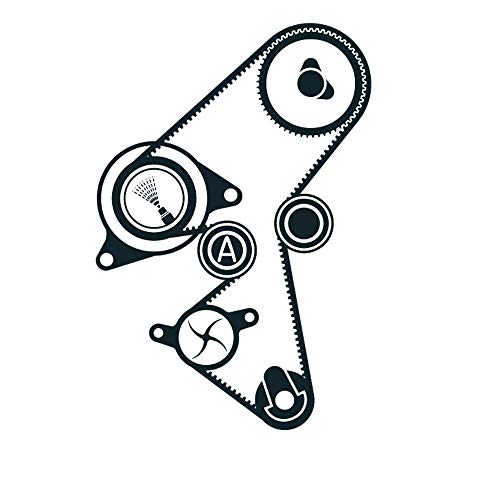
SKF VKMC 03259 Kit de distribución con bomba de agua
- Incluye todos los componentes necesarios para el reemplazo completo de la correa de distribución y la bomba de agua del motor
- Incluye correa de distribución, rodamiento de tensor y guía SKF y bomba de agua Aquamax SKF de calidad con eficiencia refrigerante equivalente a la del equipo original para desempeño optimizado
- La seguridad del vehículo es una prioridad para SKF y nuestras piezas de alta calidad están diseñadas para hacer reparaciones seguras y duraderas
- El producto debe ser instalado por mecánicos experimentados que usen las herramientas apropiadas y cumplan estrictamente con las instrucciones de SKF y las instrucciones de montaje del vehículo
- Escanee el código QR en la etiqueta de la caja del producto para acceder a las instrucciones y la información más detallada y técnica del producto SKF


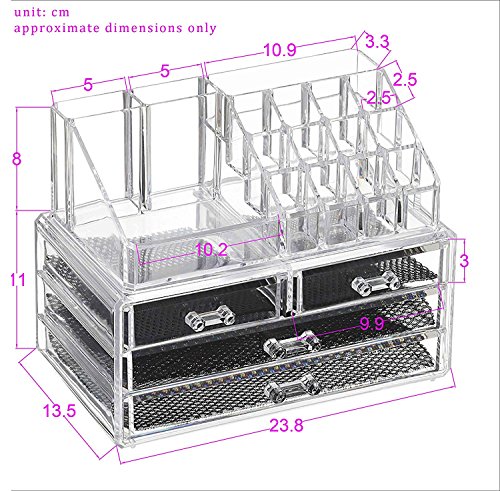
Feibrand Organizador Maquillaje Caja Cosméticos Transparente Acrílico 20 Compartimentos
- Moderna caja expositora para organizar cosméticos,4 cajones
- Diseño bonito y estilizado con estructura transparente
- Fabricada con plástico resistente y apto para alimentos
- Varios compartimentos de distintos tamaños
- También tiene espacio para objetos pequeños y bisutería


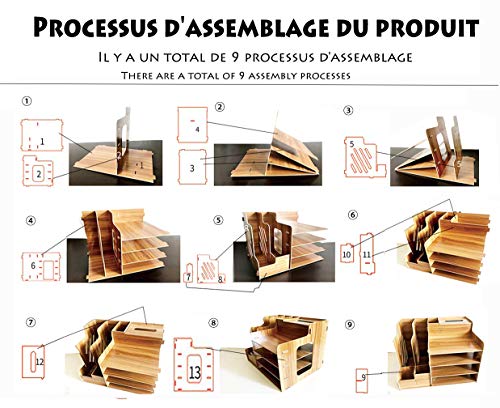
Catekro Caja de almacenamiento de escritorio de gran capacidad Porta bolígrafos/Estantería/Soporte de libros de madera
- ➤【Multifuncional】 - Hola, compre nuestra caja de almacenamiento, le enviaremos un soporte para teléfono móvil. Y la caja de almacenamiento también puede almacenar muchas cosas: archivo / papelería / revista de libros / cuaderno / cosmética, etc. Apto para hombres, mujeres, niños y ancianos.
- ➤【Fácil de ensamblar】- Simplemente ensamble los paneles en el orden en que se instalan las instrucciones. Y no tardará mucho en armar esta hermosa caja de almacenamiento. Durante el proceso, podemos reunirnos con los niños y disfrutar de la diversión del proceso de edición.
- ➤【Estructura fuerte】- Esta caja de almacenamiento de madera tiene una estructura de tornillo especial. Los tornillos se atornillan a los lados y esquinas de la placa para reforzar la caja de almacenamiento. A través del uso a largo plazo, también sentirá su practicidad.
- ➤【 Madera de calidad】-Está hecha de madera gruesa y duradera, ecológica. No es como otras maderas con un olor picante, nuestras cajas de almacenamiento no tienen olor y son fáciles para limpiar.
- ➤【Compartimento multinivel】 -2 portalápices +2 Librería + 4 compartimentos + 1 toallero de papel, puede organizar fácilmente los artículos sobre la mesa, despídase del escritorio desordenado. Puede colocarlo en la sala de estar / oficina / aula / dormitorio / sala de estudio de su hijo para que pueda disfrutar de un entretenimiento más inesperado.


Maddox Detail - Engine Dressing - Abrillantador de recubrimientos, plásticos y Gomas del Motor. (500ml)
- Abrillantador específico para motores de todo tipo
- Su fórmula devuelve el brillo e hidrata los recubrimientos plásticos del motor, manguitos, gomas, etc
- Las partes tratadas recuperan un aspecto como nuevo.
- Deja un acabado seco, no graso.
- Biodegradable


Maddox Detail - Premium Detail - Limpiador Premium de salpicaderos con abrillantador (500ml)
- Potente abrillantador y limpiador de interiores. Su lograda fórmula permite levantar la suciedad a la vez que devuelve el brillo original. Hidrata la superficie, dejando una capa protectora antiadherente al polvo, que proporciona una limpieza más detallada y duradera. Especialmente indicado para salpicaderos, plásticos, vinilo, cuero y gomas.
- Sin siliconas
- Limpia y acondiciona vinilo y cuero, plásticos y cauchos
- Hidrata y protege con con un acabado de alta calidad


Bella Aurora Doble Fuerza Crema De Belleza Mate Para Piel Mixta - 30 ml.
- Aclara la piel
- Ilumina la piel
- Ideal para piel mixta-grasa


Science4you-Perfumes Perfumes y Esencias, Súper Laboratório para Niños +8 Años, Multicolor (80002233)
- Crea fantásticos perfumes, aceites de masaje y ambientadores
- Un verdadero laboratorio de belleza para hacer perfumes y sales de baño personalizados
- Incluye esencias e ingredientes naturales para estimular la creatividad de los niños
- El regalo perfecto para las niñas de la casa
- Incluye 13 experimentos y un completísimo manual de instrucciones ilustrado con 36 páginas, para que puedas aprender todo sobre los perfumes y las sales de baño
- Fábrica de perfumes es un juego de perfumes educativo que desarrolla la imaginación y creatividad
- Edad recomendada: 8 años y más

Imágenes de Distribucion de perfumes
Si prefieres elegir de forma visual los artículos, aquí puedes observar un conjunto de fotos de distribucion de perfumes. Pincha en una de las fotos y accederás a la adquisición online de perfume en concreto viendo sus funcionalidades y valor.