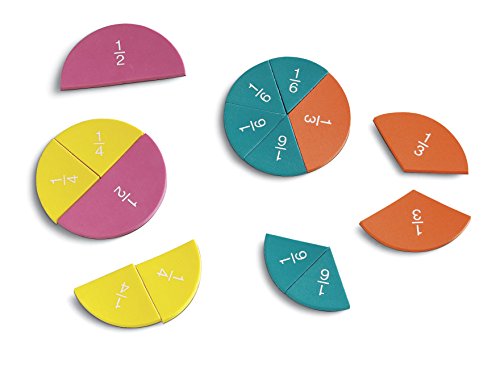Fracciones abeto
Hallar tu fragancia característica es como encontrar la pareja perfecta: Pocas veces vas a saber lo que estás buscando hasta que lo encuentres. Todavía de este modo, como en cualquier buena relación, tienes tus estándares, ¿verdad?? Tus rompecabezas, tu todo o bien nada. Mira si fracciones abeto, el abeto parte 1 o resina del abeto son tu media naranja. El mayor obstáculo para la compra de colonias online es adquirir un nuevo aroma ya antes de olerlo. Para ir sobre seguro, ten una idea de qué notas o ingredientes te gustan y cuáles no. Algunas tiendas darán una tarjeta de muestra o perfumada con la compra para probar primero antes de abrir el producto, lo que permite las devoluciones o los cambios. ¿Se ha preguntado alguna vez por qué los sumilleres se empeñan en que el vino se sostenga en un ambiente seco, eludiendo la variación de la temperatura y sosteniendo la botella fuera de la luz solar directa? Es para preservar el equilibrio de sus componentes y, como es lógico, exactamente la misma teoría se aplica asimismo a su colonia o perfume preferido.
Listado top ventas para Fracciones abeto
En este listado podrás encontrar multitud de productos como fracciones abeto perfectos para el cuidado de tu cuerpo. Toma conocimiento de que para encontrar infinidad de opciones para obtener lo mejor para tu bienestar, te encuentras en uno de los mejores sitios web del mercado.

doTerra Equilibrio 15 ml
- Promueve una sensación de relajación de cuerpo entero
- Puede ayudar a aliviar los sentimientos de ansiedad
- Evoca sentimientos de tranquilidad y equilibrio


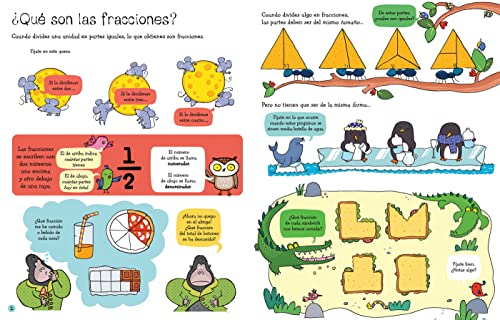
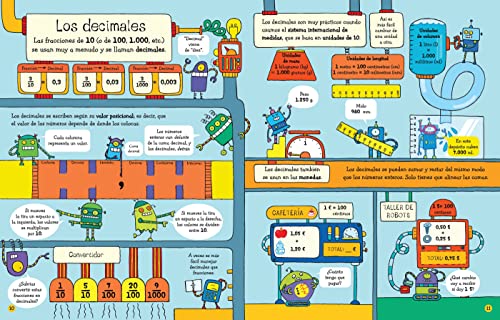
Fracciones y decimales (Solapas para aprender)


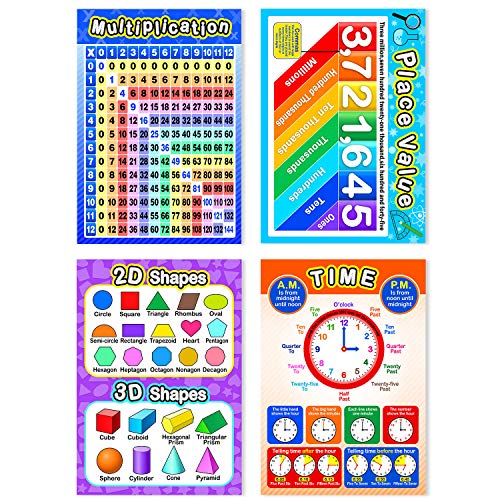
12 Piezas Póster Educativo de Matemáticas para Niños con 80 Puntos de Pegamentos para Enseñanza Primaria y Secundaria de Multiplicación División Suma Resta Fracciones Decimales, 16 x 11 Pulgadas
- 12 carteles de pared diferentes: tabla de multiplicar, división, suma, resta, números 1-100, fracciones y porcentajes, palabras clave matemáticas, números romanos, valor de posición, dinero, tiempo y formas 3D
- Características: hecho de 250 cartulina, doble cara cubierta con película PET de alta calidad para mayor durabilidad, resistente al agua, resistente al desgarro y reutilizable, también se puede secar con marcadores a base de agua para ilustrar el contenido de los carteles para una mejor expresión
- Colores e ilustraciones encantadores: diseñados con hermosos colores y elementos gráficos, capte la atención de sus hijos y las imágenes vívidas despertarán su curiosidad. Cada tamaño en 40 x 28 cm / 16 x 11 pulgadas, tamaño adecuado para niños
- Planos y fáciles de usar: no hacemos rodar nuestros carteles en tubos como muchos otros, listos para montar con el punto de pegamento que viene con el paquete, también puede colgarlos en la pared a través del agujero de la bolsa de plástico
- Gran regalo para los niños: estos carteles de educación preescolar de colores encantadores son excelentes para la educación en el hogar, preescolar, jardín de infantes, escuela primaria y secundaria. Nuestros carteles hacen que el aprendizaje sea más divertido y que atraiga la atención de su niño, y las imágenes vívidas despertarán su curiosidad.


Learning Resources Rainbow Fraction Bingo
- Juego sencillo estilo bingo
- Ayuda a aprender a reconocer las fracciones y sus equivalencias
- Presenta dos niveles de juego
- Incluye guía de actividades multilingüe y empaque
- Está codificado por color para usarlo con otros juegos y recursos rainbow fraction de learning resources


Learning Resources- Divertido Juego de fracciones Pizza Fraction Fun, Color (LER5060)
- Actividades prácticas y divertidas de fracciones
- Fomenta la práctica de la suma y resta de fracciones
- Refuerza las equivalencias hasta los dieciseisavos
- Para 2-4 jugadores
- Las porciones son de gran tamaño


Learning Resources- Piezas fraccionarias magnéticas de Espuma Blanda Rainbow Fraction, Color (LER0611)
- Exploración práctica de las fracciones
- Ideal para aprender a sumar y a restar fracciones y también a compararlas
- Presenta un fondo magnético
- Conjunto de 51
- Las piezas están hechas de espuma blanda


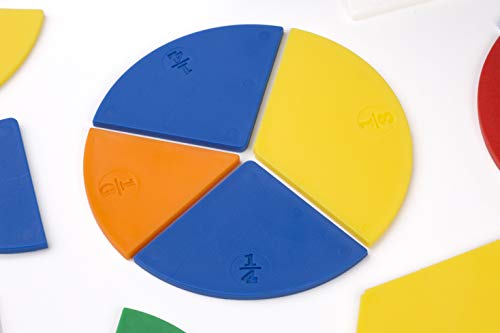
Miniland- Set Fracciones para Juegos matemáticos (95218)
- Divertida visión de las fracciones
- Aprendizaje ameno del mundo de las fracciones
- A través de situaciones cotidianas
- Material de gran calidad y durabilidad
- Incluye guía didáctica
- Número de jugadores: 1


Learning Resources Resources-LER2509 Conjunto de equivalencia de Cubos Fraction Tower, Color (LER2509)
- Una manera atractiva, práctica para reforzar las fracciones en casa
- Coloridas, cubos entrelazados duraderos son perfectos para explorar y comparar fracciones
- Para el uso con el gráfico de la fracción
- Hacer fracciones fácil
- Adecuado para niños de seis años o más


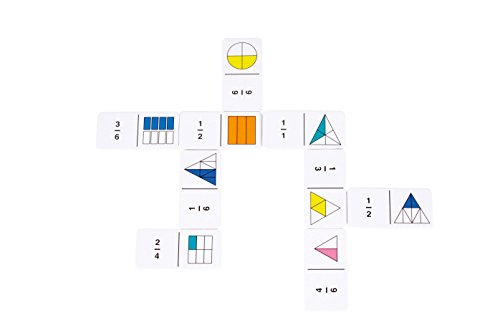
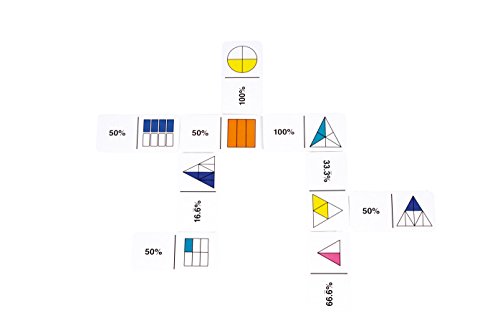
Fichas de dominó con fracciones Rainbow Fraction de Learning Resources
- Dominó fracciones


Learning Resources- Círculos magnéticos de Espuma Blanda Rainbow Fraction, Color (LER0608)
- Exploración práctica de las fracciones
- Ideal para aprender a sumar y a restar fracciones y también a compararlas
- Presenta un fondo magnético
- Conjunto de 51
- Las piezas están hechas de espuma blanda


BRUBAKER 101-piezas de Bolas de Navidad con Copas de árboles Rojos
- 100 hermosas e irrompibles bolas de árbol de Navidad de plástico resistente y una tapa árbol de Navidad!
- Bolas de árbol tradicionales en 3 tamaños diferentes, paquetes de regalo, piñones de abeto y campanas
- 3 versiones diferentes: brillante, con destello brillante y mate
- El XXL Complete Set para el árbol de Navidad perfecto o para los arreglos navideños en interiores y exteriores
- Alta calidad y buen acabado

Imágenes de Fracciones abeto
Puedes ver aquí una agrupación de fotografías de fracciones abeto para que te hagas una idea y puedas escoger entre todos los modelos de colonia. Pincha en una de las imágenes para ver la ficha entera del artículo y su coste.