Marcas tales como
Un perfume va a ser la primera cosa que busques ya antes de salir por la puerta, y un aroma que disfrutarás todo el día. Para ayudarte a localizar una nueva fragancia para añadir a tu rutina diaria, hemos encontrado las mejores fragancias, como marcas tales como, 10 corso como o bien violeta como, que los críticos adoran por sus aromas universalmente agradables. Ya que estás comprando un perfume, completa tus compras de fragancias consultando nuestras tiendas de belleza on line favoritas a fin de que puedas refrescar toda tu colección de belleza. Depende totalmente de nuestros recuerdos si un olor nos llega o bien no a la psique, lo que explica por qué ciertos de nosotros estamos conmovidos por un soplo de hierba recién cortada o bien de gasolina, mientras que otros. No tanto.
Listado top ventas para Marcas tales como
Aquí encontrarás multitud de productos como marcas tales como muy buenos para el cuidado de tu bienestar. Vamos a ayudarte a encontrar los mejores modelos, a tener la posibilidad de comparar precios y alcanzar la mejor opción para tu bienestar.

Fabula


Inquebrantables


Resiliencia: Ejercicios útiles y eficaces para combatir el estrés, los problemas y posibles contratiempos (Guiadas para la Relajación)


Encuentro de almas I: Por Clara (Bilogía Encuentro de almas nº 1)


Luke. Liberación (Chicago Cops nº 2)


No soy ese hombre

![The Neighbors - Season 2 [Ultra HD] The Neighbors - Season 2 [Ultra HD]](https://www.iesribera.es/pics/2020/10/03/the-neighbors-season-2-ultra-hd-250386.jpg)
The Neighbors - Season 2 [Ultra HD]


Cómo publicar un libro sin editoriales chupasangre: Guía de 7 pasos para autopublicar un libro en Amazon (Triunfa con tu libro nº 2)


Tal Como Soy


Tal y Como Es (feat. Marces)


MARCO de PLATA bilaminada PARA COMUNION, lleva un Kit incluido con el que se puede Personalizar el Marco tal y como se refleja en la foto.
- Marco de fotos para Comuniones.
- Plata. La parte posterior ó trasera está acabada en madera color Cerezo.
- MEDIDA: 13X18 CMS.
- SE ENVIA PREPARADO PARA REGALO


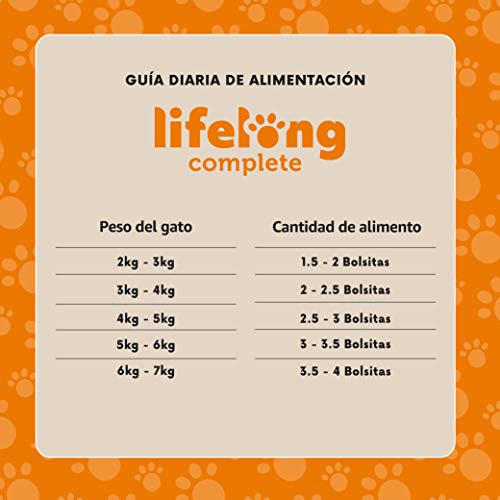
Marca Amazon - Lifelong Alimento completo para gatos adultos - Selección mixta en salsa, 2,4 kg (24 bolsitas x 100g)
- El envase contiene 24 porciones: 6 x bocaditos con vacuno en salsa; 6 x bocaditos con pollo en salsa; 6 x bocaditos con salmón en salsa; 6 x bocaditos con bacalao en salsa
- Comida para gatos adultos: nutrición 100% completa y equilibrada Diseñada por nutricionistas de animales y revisada por veterinarios
- Carne y derivados cárnicos 32% (incluido un mínimo de 4% de la proteína mencionada). Carne y derivados de origen animal aptos para el consumo humano
- El producto contiene "azúcares variados", derivados del sirope de caramelo utilizado como fuente natural de color (0,15%); no se han añadido otros azúcares.
- Prebióticos naturales para mejorar la digestión sensible; con taurina para tener la vista y el corazón con buena salud
- Con fibra (inulina) para favorecer la digestibilidad; con biotina que aporta brillo al pelaje
- Con vitamina D3 para mejorar la salud de los huesos y dientes; con vitamina E para ayudar a mantener una buena función inmunológica
- Sin aromas, colorantes ni conservantes artificiales. Sin soja, cebada o productos lácteos añadidos. Una receta sabrosa con proteínas de alta calidad
- Divida cada bolsa en 2 comidas al día. Las madres embarazadas y en lactancia pueden necesitar hasta 4 veces más. Asegúrese siempre de que haya agua potable disponible
- Almacenar en un lugar fresco y seco. Una vez abierto, mantener refrigerada y utilizar en un plazo de 2 días


Tal y Como Es (feat. Marces)


Hand of God Season 2


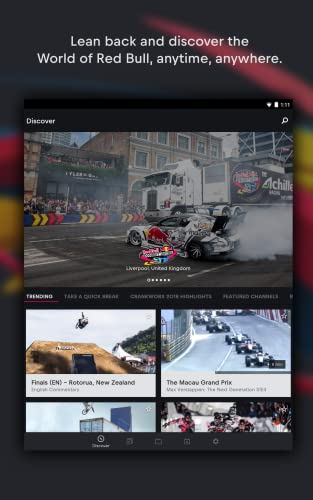
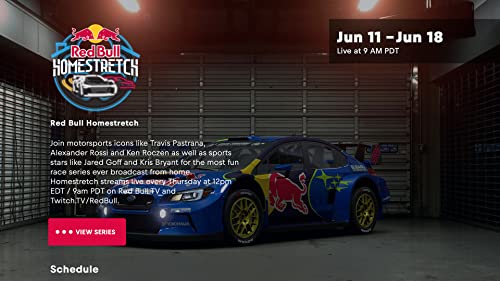
Red Bull TV
- Create a user login to support: offline viewing, favorites, custom playlists
- Access to a wide-ranging library of HD content
- Weekly live events
- 24/7 Best of Red Bull TV channel


Kindle, ahora con luz frontal integrada, blanco
- La luz integrada regulable te permite leer durante horas dentro y fuera de casa, tanto de día como de noche.
- Diseñado para la lectura: dispone de una pantalla de 167 ppp y alto contraste en la que se lee como en papel impreso, sin ningún reflejo, incluso bajo la luz del sol.
- Lee sin distracciones. Subraya pasajes, busca definiciones, traduce palabras o ajusta el tamaño del texto: todo ello sin abandonar la página que estás leyendo.
- Elige entre millones de libros. Tiene capacidad para miles de títulos, así que siempre podrás llevar tu biblioteca contigo.
- Los miembros Prime tienen acceso a cientos de libros.
- Una sola carga y la batería dura semanas, no horas.


Diccionario De Primaria (Vox - Lengua Española - Diccionarios Escolares) - 9788499742106


Amazon para Tablets
- Encuentra rápidamente detalles de producto y lee opiniones de millones de productos vendidos por Amazon.es y otros vendedores de la plataforma
- Aprovecha las ventajas de los pedidos en 1-clic, soporte para miembros Premium, Listas de deseos, seguimiento de pedidos y más
- Compra con confianza, sabiendo que todas las transacciones se procesan de forma segura
- Disponible para tablets Android de 7 a 10 pulgadas, con resoluciones entre 600x1024 a 1600x2560, con la versión del sistema operativo Android 4.0.3 o superiores.

Imágenes de Marcas tales como
Tienes aquí una agrupación de fotos de marcas tales como para que te formes una idea y puedas escoger entre todos los modelos de perfume. Pincha en una de las fotos para ver la ficha íntegra del producto y su precio.