Leccion traduccion
Un aroma característico ha de ser intemporal y llevable, en cualquier situación y a cualquier edad. Pero como es natural, con tantas olores como leccion traduccion, self tan traduccion o dew traduccion en el mercado, hallar el perfume perfecto para ti puede ser un reto. Depende absolutamente de nuestros propios recuerdos si un fragancia nos llega o bien no a la mente, lo que explica por qué ciertos de nosotros estamos emocionados por un soplo de yerba recién cortada o de gasolina, mientras que otros. No tanto. Una forma de saber si un perfume te gustará seguramente es probar los que han existido durante años y han resistido el correr del tiempo. Fragancias conocidas como Daisy de Marc Jacob y el Número 5 de Chanel tienen una religión que sigue una explicación: son impresionantes.
Listado top ventas para Leccion traduccion
Aquí podrás encontrar numerosos productos como leccion traduccion perfectos para el cuidado de tu bienestar. Te ayudaremos a encontrar los mejores modelos, a tener la posibilidad de comparar precios y conseguir la mejor opción para tu cuerpo.

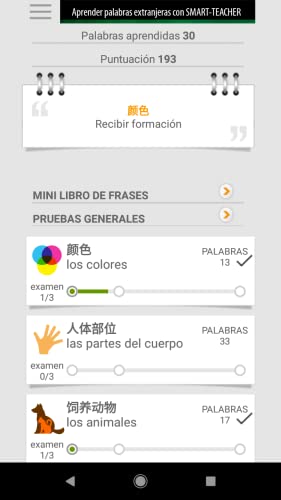
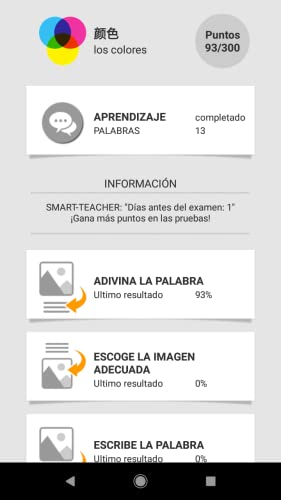
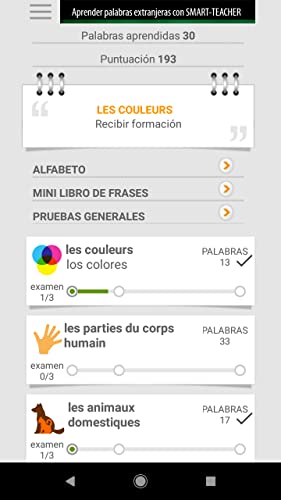
Aprender palabras en chinas con Smart-Teacher
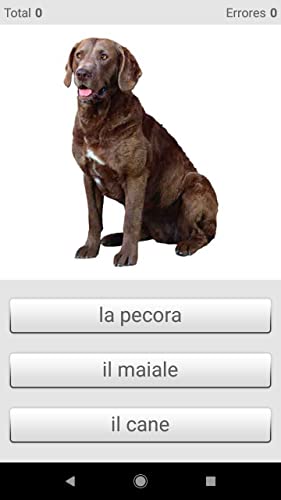
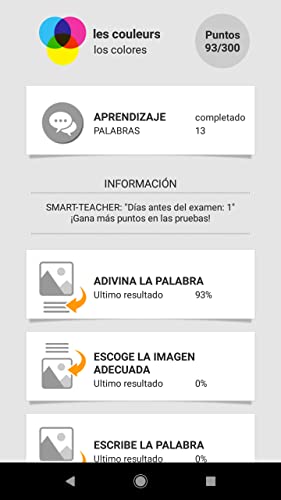
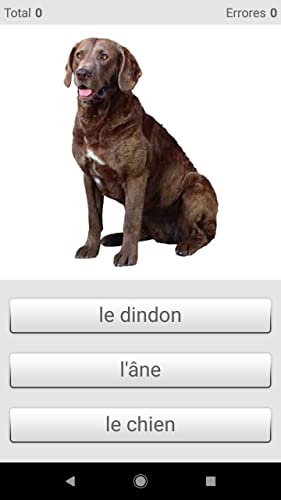
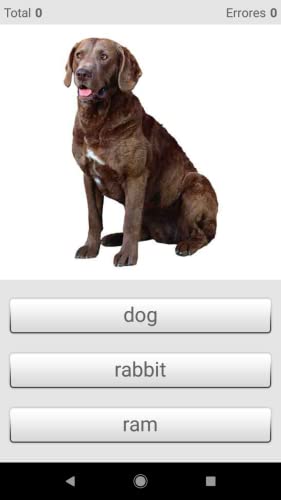
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
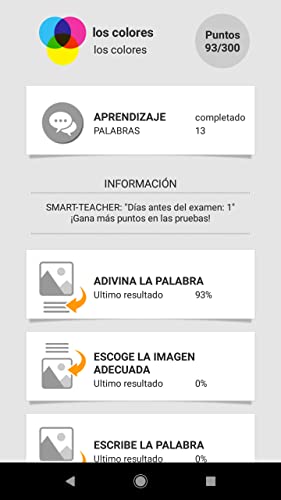
- Writing words and spell check.


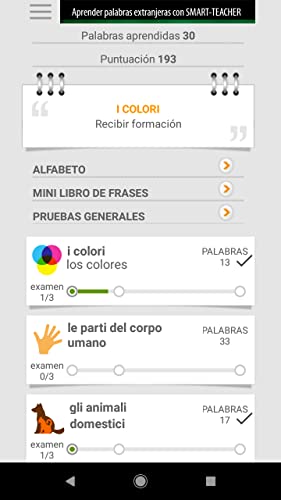
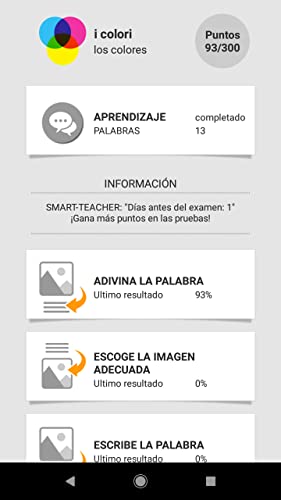
Aprender palabras en italiano con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.


25 lecciones que he aprendido sobre fotografia...la vida: traducción al castellano de Daniel Miguelánez (25 Lessons I've Learned About Photography...Life!)


Literatura y traducción: (Apuntes TraLiterarios) (Lecciones de cosas)
- Diseño creativo
- Calidad óptima para los requisitos del cliente
- Producto por tu tiempo libre
- Creado para un uso prolongado


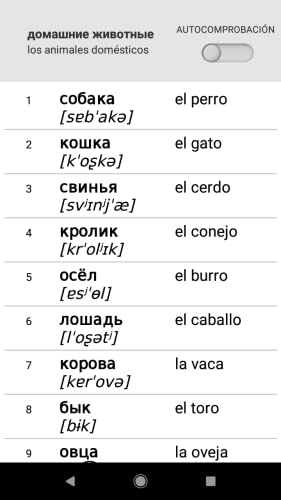
Aprender palabras en ruso con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.


Aprender palabras en español con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.


Aprender palabras en inglés americano con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.


Aprender palabras en alemán con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.


Aprender palabras en francés con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.


Aprender palabras en inglés con Smart-Teacher
- Choosing the right word for the picture.
- Choosing the dynamic moving images for the words.
- Writing words and spell check.

![El Joven Lincoln Blu-Ray [Blu-ray] El Joven Lincoln Blu-Ray [Blu-ray]](https://www.iesribera.es/pics/2020/09/17/el-joven-lincoln-blu-ray-blu-ray-42874.jpg)
El Joven Lincoln Blu-Ray [Blu-ray]


El hombre en busca de sentido


El hombre en busca de sentido


Aprenda Palabras en Español Gratis: Lecciones de juego de Vocabulario usando Tarjetas Flash
- Aprenda palabras de la lengua española a nivel de lectura de un preescolar.
- Pruebe 3 de las 12 categorías de palabras totalmente gratis.
- Narración en español clara.
- Opción para mostrar ya sea 2 o 4 imágenes en tarjetas flash a la vez para que tenga un juego simple o más avanzado.
- Apto para todas las edades.


Sapiens. De animales a dioses: Una breve historia de la humanidad


Padre rico. Padre pobre (Nueva edición actualizada).: Qué les enseñan los ricos a sus hijos acerca del dinero

Imágenes de Leccion traduccion
Si quieres elegir de forma visual los productos, puedes ver aquí un montón de fotos de leccion traduccion. Haz click en una de las imágenes y pasarás a la compra online de perfume en concreto viendo sus propiedades y coste.