El verdadero gentleman
Para asistir a guiar tu búsqueda, es una gran idea meditar en las fragancias conforme a las diferentes categorías: florales, frutales, madereras o limpias, en tanto que la mayor parte de la gente se inclina innatamente cara una de ellas. Eso te va a ayudar a reducir las opciones, cuando menos un poco y podrás enfocarte en productos más atractivos para ti como el verdadero gentleman, the one gentleman o bien gentleman edp. He visto aun pequeños impresionados por los olores agradables. Si es necesario que elijas el mejor perfume o sencillamente vas a la tienda a seleccionar las fragancias con mejor fragancia, se convierte en un reto. Hay muchas cosas que verás frente a ti, mas tomar la decisión de adquirir una va a ser imposible. Debido a la gran cantidad de opciones, puede ser abrumador. ¿Pero de qué manera sabes en qué momento has encontrado la mejor colonia para ti? Vas a reconocer tu aroma característico cuando lo huelas. Es un poco como el amor: Escoge la que atraiga más cumplidos. Tú, y la gente que te circunda, deberían gozar del aroma.
Listado top ventas para El verdadero gentleman
Deseamos que con este listado de productos puedas encontrar el verdadero gentleman al mejor precio y mejor calidad para el cuidado y bienestar de tu bienestar. Te ayudaremos a localizar los mejores modelos, a tener la posibilidad de comparar precios y alcanzar la mejor opción para tu cuerpo.

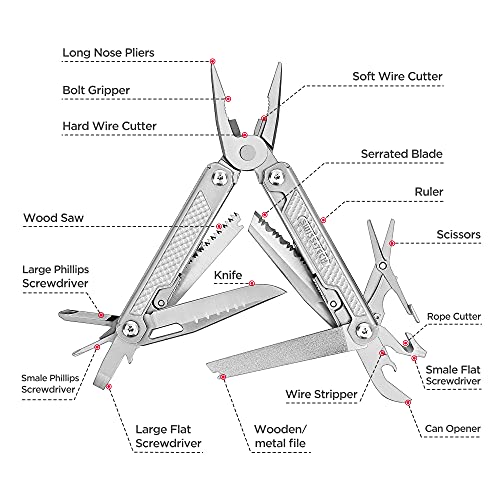
Swiss+Tech Alicate Multiuso 17 en 1, Navaja Multiusos, de Acero Inoxidable, Multiherramienta,Alicates Plegables, Multifunción con Alicates, Navaja, Sierra para Acampada, Caza, Senderismo,etc
- 【Alicates multiusos 17 en 1】 Alicates multiusos Incluye cortador de alambre, cuchillo,destornillador, sierra, lima, abrelata y tijeras. Puede satisfacer sus diferentes necesidades diarias, ya no tiene que preocuparse por no encontrar la herramienta adecuada.
- 【Seguro y cómodo de usar】 El diseño de bloqueo de seguridad hace que abrir y cerrar la herramienta sea más fácil y seguro para reducir el riesgo de lesiones durante el uso. Además, su mango es muy cómodo de sujetar, reduciendo eficazmente la fatiga durante el uso.
- 【Robusto y duradero】 El alicate multiuso está hecho de acero inoxidable de alta calidad. Después del tratamiento térmico, muestra una alta dureza y buena resistencia al desgaste. Está libre de óxido y tiene una larga vida útil, lo que es muy adecuado para su uso en el campo.
- 【Ligero y portátil】 El tamaño del alicate multifunción es de 160 mm cuando está completamente abierto y de 100 mm cuando está completamente plegado, el peso es de solo 265 g, por lo que no se sentirá pesado incluso si lo lleva consigo.
- 【Amplia aplicación】 Es una verdadera herramienta multiusos de bolsillo, con 17 herramientas para todo trabajo. Adecuado para casi todos los requisitos del uso diario, ideal para acampar, pescar, hacer senderismo, cazar, sobrevivir, bricolaje y otras actividades al aire libre.


Pluma Estilográfica Deep Crimson Red de Scriveiner – Plumilla (mediana) y Convertidor Instalado Schmidt, Incluye Dos Cartuchos de Tinta, Azul y Negro
- ★DISFRUTA DE LA SENSACIÓN DE UNA VERDADERA PLUMA DE LUJO EN TU MANO: Impresionante pluma estilográfica de Scriveiner hecha de latón con un acabado lacado rojo y detalles cromados. Calidad premium y lujo discreto de una boutique de marca inglesa.
- ★TRANSCRIBE TUS PENSAMIENTOS SIN ESFUERZO: Tu pluma de caligrafía viene con una plumilla mediana Schmidt adornada en oro de 18 quilates. Cuenta con un convertidor Schmidt instalado y dos cartuchos de tinta de repuesto, uno azul y otro negro. El sistema de tinta Schmidt de Alemania permite que la plumilla de escritura se deslice suavemente sobre cualquier tipo de papel. Su peso perfectamente equilibrado y balanceando te proporciona una mayor comodidad al escribir.
- ★IMPRESIONA A TUS COLEGAS Y SERES QUERIDOS: La pluma estilográfica elegante de Scriveiner viene en una hermosa caja de presentación que la hace el regalo perfecto. Ya sea como una pluma casual o ejecutiva, para el trabajo, para la oficina o para uso personal, tu pluma estilográfica Scriveiner será admirada por quienes te rodean.
- ★EXPRESA ELEGANCIA, SOFISTICACIÓN Y LUJO DISCRETO: Los bolígrafos estilográficos Scriveiner son diseñados en Londres, Inglaterra; comparten los atributos atemporales del diseño británico clásico.
- ★COMPRA CON TOTAL CONFIANZA: Servicio al cliente increíble y garantía de devolución del 100% del dinero. Nuestros clientes son el centro de todo lo que hacemos. Si no estás satisfecho, lo remplazaremos o le reembolsaremos, lo que prefieras. Conocemos la calidad de nuestros productos y deseamos que tengas lo mejor posible.


TROIKA DISTRUCTION PIP20SI/RD - Bolígrafo, reglas, escalas, nivel de burbuja, destornillador de punta plana y de cruz, lápiz rojo, mina negra, lacada, plateado/rojo
- Bolígrafo, ayuda de planificación y maletín de herramientas en uno.
- Idea de regalo ideal para arquitectos, planificadores, dibujadores técnicos, ingenieros.
- El bolígrafo tiene una mina negra y una longitud de escritura de 1600 hasta 1800 m.
- Con diferentes escalas, regla de centímetros y pulgadas, destornillador de estrella/estrella, lápiz capacitivo y nivel de burbuja (diámetro: 10 mm).
- El bolígrafo también tiene una regla en centímetros y pulgadas, un nivel de burbuja y un destornillador de cabeza plana y de estrella.


Master of Chess GENTLEMAN 50 x 50 x 3 cm Ajedrez de madera grande para adultos y niños tablero de ajedrez hecho a mano y piezas (50 x 50 x 3 cm borde blanco)
- Estas hermosas piezas de ajedrez de estilo género están hechas de madera de viga de cuerno. Este juego incluye un tablero de ajedrez plegable, tamaño 50 x 25 x 6 cm, con un inserto para figuras en el interior.
- El tablero de ajedrez está hecho de madera, pintado y barnizado. Dentro de la cassette, las piezas de ajedrez están dispuestas especialmente para este modelo de un elegante forro verde moldeado. Las piezas de ajedrez y el casete se producen completamente en Polonia y se fabrican con el máximo cuidado.
- El juego de ajedrez de Navidad garantiza una gran diversión, un buen tiempo y una verdadera relajación para todos aquellos que les gusta el entretenimiento intelectual. También son el regalo perfecto para cualquier ocasión.
- Tamaño del tablero de ajedrez: 50 x 50 x 3 cm. Tamaño King: 120 mm
- Este es solo uno de los muchos de nuestros artículos de calidad. Consulta nuestra oferta para más información


TROIKA CONSTRUCTION PIP20/BG - Bolígrafo multitarea (regla en centímetros y pulgadas, escala 1:20 m y 1:50 m, nivel de burbuja, destornillador plano y de estrella), color negro y dorado
- Bolígrafo, ayuda de planificación y maletín de herramientas en uno
- Idea de regalo ideal para arquitectos, planificadores, dibujadores técnicos, ingenieros
- El bolígrafo tiene una mina negra y una longitud de escritura de 1600 hasta 1800 m
- Con diferentes escalas, regla de centímetros y pulgadas, destornillador de estrella/estrella, lápiz capacitivo y nivel de burbuja (diámetro: 10 mm)
- El bolígrafo también tiene una regla en centímetros y pulgadas, un nivel de burbuja y un destornillador de cabeza plana y de estrella


BÖKER Hombre Urban Trapper Damasteel Navaja, Gris, One Size
- Longitud total: 19, 5 cm/Longitud de la hoja: 8, 7 cm/Grosor de la hoja: 2, 5 mm
- Peso: 48, 0 g
- Material de la hoja: acero de Damasco
- Mango material: titanio
- Ayuda de apertura: Flipper/Cierre: Frame Lock


Cojín de huesos de cereza extra largo de 350 gramos para el bienestar de la relajación para calentar en el horno o microondas, huesos de cereza de 350 gramos, 42cm x 12cm (Gentleman)
- Contra el dolor: la almohada de carozos de cereza cuadrada (42 x 12 cm) para poner en el hombro, la parte posterior o los pies, para el calor, el frío y el tratamiento de la tensión en caso de fatiga, de dolor abdominal, de fríos, de tensiones, de contusiones o de inflamación.
- Natural: agradable ambiente, aroma de apoyo a la curación: los núcleos de cerezo ideal para regalar una óptima Almacenamiento y reproducción de su propio calor corporal, ya que no tiene ningún cereal es también apto para alérgicos.
- Fácil de usar: calentar en el horno y en el microondas, conservación del calor, cómodo de poner mediante la distribución uniforme del relleno del cojín. Envasado hermético.
- Durable: la tela sólida y durable, producida según el estándar 100 de Öko-Tex tiene una larga vida útil.
- -


Scriveiner Pluma Estilográfica Plateada con Detalles de Oro de 24k y 18K para una Caligrafía Suave y Elegante, Plumilla (EF) y Convertidor Instalado Schmidt, Dos Cartuchos de Tinta, Azul y Negro
- ★ DISFRUTA DE LA SENSACIÓN DE UNA VERDADERA PLUMA DE LUJO EN TU MANO: Impresionante pluma estilográfica de Scriveiner hecha de latón con acabado cromo plateado y detalles de oro de 24 quilates. Calidad premium y lujo discreto de una boutique de marca inglesa.
- ★TRANSCRIBE TUS PENSAMIENTOS SIN ESFUERZO: Tu pluma de caligrafía viene con una plumilla mediana Schmidt adornada en oro de 18 quilates. Cuenta con un convertidor Schmidt instalado y dos cartuchos de tinta de repuesto, uno azul y otro negro. El sistema de tinta Schmidt de Alemania permite que la plumilla de escritura se deslice suavemente sobre cualquier tipo de papel. Su peso perfectamente equilibrado y balanceando te proporciona una mayor comodidad al escribir.
- ★IMPRESIONA A TUS COLEGAS Y SERES QUERIDOS: La pluma estilográfica elegante de Scriveiner viene en una hermosa caja de presentación que la hace el regalo perfecto. Ya sea como una pluma casual o ejecutiva, para el trabajo, para la oficina o para uso personal, tu pluma estilográfica Scriveiner será admirada por quienes te rodean.
- ★EXPRESA ELEGANCIA, SOFISTICACIÓN Y LUJO DISCRETO: Los bolígrafos estilográficos Scriveiner son diseñados en Londres, Inglaterra; comparten los atributos atemporales del diseño británico clásico.
- ★COMPRA CON TOTAL CONFIANZA: Servicio al cliente increíble y garantía de devolución del 100% del dinero. Nuestros clientes son el centro de todo lo que hacemos. Si no estás satisfecho, lo remplazaremos o le reembolsaremos, lo que prefieras. Conocemos la calidad de nuestros productos y deseamos que tengas lo mejor posible.


GENTLEMAN SYLT Neceser transparente | equipaje de mano | 1 litro Premium para seguridad | neceser transparente | con caja de regalo, Blanco (Blanco) - BOARDING
- Neceser de cultura: ya sea en un viaje en avión, en casa o en un viaje de fin de semana, el neceser transparente es un compañero elegante y un verdadero punto de atracción.
- Organizador versátil: ya sea como bolsa de maquillaje o bolsa de lavado, la bolsa de aseo es versátil y ofrece espacio para todo tipo de artículos de higiene y cosméticos.
- Funcional: la bolsa de cosméticos es impermeable y dispone de un asa con mosquetón. Esto permite colgar el neceser tanto longitudinal como transversal.
- Compañero de viaje: guarda pequeños utensilios de viaje como, por ejemplo, productos para el cabello, el cuerpo y el cuidado del cepillo de dientes de forma segura y protegida en nuestra bolsa de aseo de alta calidad.
- Dimensiones: el neceser mide 21 cm de largo, 4 cm de ancho y 12 cm de alto y es ideal para viajes en avión. La bolsa ofrece espacio para aproximadamente 1 l de contenido y puede soportar hasta 3 kg.


Schwarzkopf Got2b fenomenal 100ml Moldeo Pega - Paquete de 6
- Efecto: crea peinados de larga duración con la pasta de moldeo engrosamiento para un acabado limpio y natural con brillo, descubre al verdadero caballero que hay en ti
- El pedido incluye: 6 pasta de moldeo fenomenal Schwarzkopf got2b (100 ml)
- Sujeción: el producto de aseo para el cabello proporciona una sujeción duradera; prepárate para convertirte en un caballero fenómenal
- Tecnología: el tratamiento del cabello con cera natural, polímeros de peinado y copolímeros crea una sujeción y un aspecto más completo mientras protege el cabello de la sequedad
- Cómo lucir fenómenal: utiliza una cantidad razonable de pasta y frota en la palma de tus manos, aplica sobre el cabello seco


Juego de espresso de esmalte para caballeros
- Este juego viene con dos tazas de esmalte espresso en color crema con bordes azules.
- Un lado tiene el emblemático logotipo de Gentlemen's Hardware, mientras que el otro lado tiene el otro símbolo icónico de Gentlemen's Hardware – la cita 'The Adventure Begins" debajo de una ilustración de montañas.
- Cada taza tiene una capacidad de 5.5 onzas y un diámetro de aproximadamente 7.0 cm.
- Lavar en detergente suave antes de usar y lavar a mano. Tenga cuidado al usar esto con bebidas calientes ya que las tazas pueden calentarse.
- Ambas tazas vienen en un embalaje de regalo kraft de 10,9 x 18,5 x 7,4 cm.


Rainbow Socks - Hombre Calcetines Caballero Regalo - 3 Pares - Talla 41-46
- EL MUNDO DE LOS HOMBRES – Todo el mundo le gusta mostrar su pasión. Calcetines con el patrón adecuado son la forma ideal de acentuar los intereses. Los amantes del whisky amarán su color sobre un fondo negro. Un estilista aficionado o un peluquero profesional notará la forma perfecta de bigote en una tela amarilla. Cuando un experto en cigarros usa los calcetines azul marino, se irá inmediatamente a Cuba con pensamientos. Gentleman Socks Box: te ayudarán a convertirte en un verdadero caballero!
- CALCETINES ELEGANTES PARA HOMBRES- Gentelman Socks Box es una propuesta para hombres que aman el estilo y la comodidad y que les gusta subrayar su carácter. Estos calcetines de algodón están de moda y serán ideales para el trabajo, para reuniones con amigos o para llevarlos en casa. Van bien con casi todos los pantalones: jeans, chino, etc. El delicado ribete no oprime tus piernas. Un conjunto de 3 pares está disponible en dos tamaños: 41-46.
- REGALO ATRACTIVO - Se acerca el cumpleaños de tu novio? O el guardarropa de tu marido necesita una actualización ? Cada situación de este tipo es una oportunidad para complacer a su amigo y darle calcetines creados especialmente para hombres! También serán una buena opción para el Día del Padre. Los calcetines ya están elegantemente empaquetados en una caja de buen gusto que puedes dar inmediatamente. Cualquier hombre, joven o viejo, apreciará tal gesto!
- FABRICADOS EN EUROPA- Ladies Socks Box es nuestro proyecto original que realizamos en nuestra fábrica familiar en Europa Central. Producimos calcetines durante generaciones, por lo que podemos presumir de una gran pasión y experiencia. Hacemos estos calcetines en algodón peinado de alta calidad y por eso el pie respira libremente durante todo el día. Nuestro hilo está certificado por OEKO-TEX y eso garantiza la seguridad y el confort del uso de estos calcetines.
- PATRONES TEJADOS- los patrones coloridos de calcetines han dominado el mercado y los armarios durante mucho tiempo. Nada nuevo, pueden hacer un calcetín ordinario para calcetin de nuestra estilización. Cosemos todos nuestros modelos con hilos de colores y no los imprimimos. Como resultado, son más duraderos y no desaparecerán después de algunos lavados. Además, son más suaves y agradables al tacto. Estos calcetines no solo son estéticos, sino también funcionales.


Gentlemen Hardware - Herramienta de manicura de bolsillo para hombre, color negro
- Esta herramienta de manicura de acero inoxidable de tamaño bolsillo incluye cortauñas 4 en 1, tijeras y una lima de uñas.
- Incluye un práctico mosquetón para que el producto se pueda fijar a una bolsa o llavero.
- Tamaño de bolsillo
- Los productos de hardware para caballeros han sido fabricados para los rigores de la vida moderna de hoy: productos verdaderamente excelentes fabricados por pioneros implacables.
- Empaquetado en una lata de inspiración vintage y perfecto para regalar.


Conjunto de Cuatro Piezas para Bebé Niño Ropa Gentleman Camisa de Manga Larga Corbata de moño + Chaqueta + Pantalones Traje de Bautizo Fiesta Boda Trajes(Verde,12-18 Meses)
- Material agradable para la piel: nuestro conjunto de ropa para bebés hecho de algodón 100% orgánico garantiza una sensación táctil suave y acogedora, ofrece un ajuste perfecto cada vez, no se deformará fácilmente, se amontonará, agradable a la delicada piel del bebé.
- El paquete incluye:1 camisa + 1 pajarita + 1 tirantes + 1 pantalón.
- Tamaño para: 4-7 meses / 6-9 meses / 9-12 meses / 12-18 meses / 18-24 meses / 2-3 años / 3-4 años bebé.
- Equipado con una linda pajarita y un mono, haz que tu bebé sea un verdadero caballero y acompaña a tu bebé a crecer sano y feliz.
- Entrega rápida: administrado por Amazon. Brindarle una experiencia de compra rápida y un buen servicio. Si tiene alguna pregunta, no dude en contactarnos.

Imágenes de El verdadero gentleman
Aquí tienes una galería de imágenes de el verdadero gentleman para que te hagas una idea y puedas seleccionar entre todos los tipos de colonia. Pincha en una de las fotografías para ver la ficha completa del producto y su valor.