El teorema de Pitágoras es uno de los conceptos fundamentales de la geometría. A lo largo de la historia, ha sido utilizado para resolver una amplia variedad de problemas y ha desempeñado un papel crucial en el desarrollo de esta disciplina. En este artículo, exploraremos el propósito del teorema de Pitágoras y cómo su comprensión puede abrir las puertas a un mundo fascinante de formas y figuras. Si alguna vez te has preguntado cómo funciona este teorema y por qué es tan importante, ¡sigue leyendo para descubrirlo!
La finalidad del teorema de Pitágoras y su importancia en la geometría
La finalidad del teorema de Pitágoras y su importancia en la geometría
El teorema de Pitágoras es uno de los conceptos fundamentales en la geometría. Fue descubierto por el matemático griego Pitágoras en el siglo V a.C. y desde entonces ha sido un pilar en el estudio de las relaciones entre los lados de un triángulo rectángulo.
**¿En qué consiste el teorema de Pitágoras?**
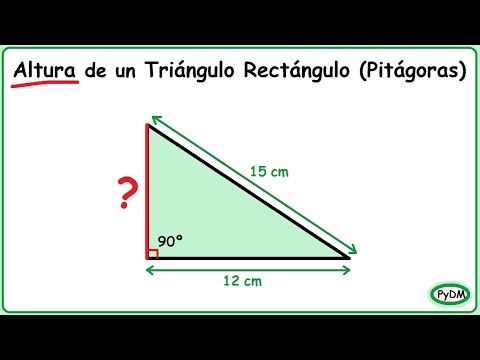
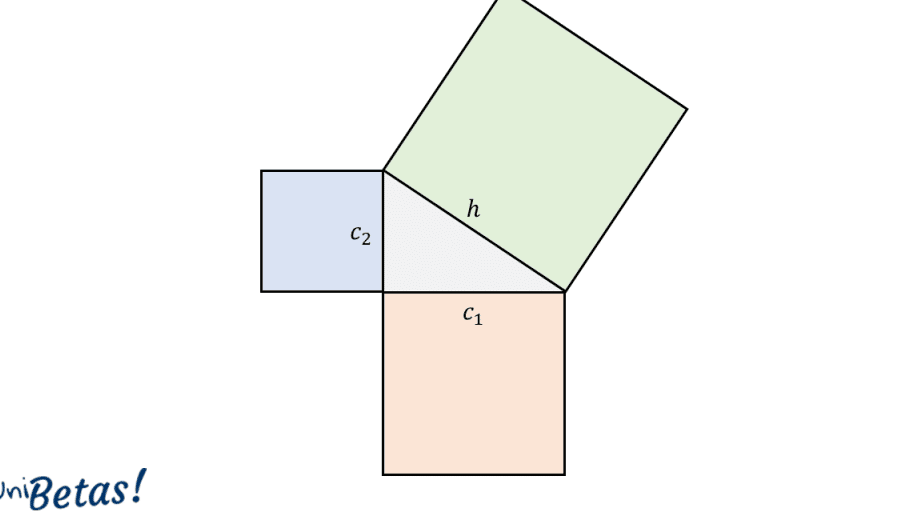
El teorema establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Matemáticamente, esto se expresa como: a^2 + b^2 = c^2, donde «a» y «b» son las longitudes de los catetos y «c» es la longitud de la hipotenusa.
**Finalidad del teorema de Pitágoras**
La finalidad del teorema de Pitágoras es permitir el cálculo de la longitud de un lado desconocido en un triángulo rectángulo, siempre y cuando se conozcan las longitudes de los otros dos lados. Esto es de gran importancia en la geometría y en diversas aplicaciones prácticas, como la arquitectura, la ingeniería y la navegación.
**Importancia en la geometría**
El teorema de Pitágoras es esencial en la geometría porque permite resolver problemas relacionados con triángulos rectángulos. Al conocer la longitud de dos lados, se puede determinar la longitud del tercer lado de manera precisa. Esto es especialmente útil en el cálculo de distancias, áreas y volúmenes en la geometría euclidiana.
Además, el teorema de Pitágoras es la base para el desarrollo de otros conceptos geométricos, como el seno, coseno y tangente de un ángulo, así como las identidades trigonométricas. Estas herramientas matemáticas son utilizadas en campos como la física, la ingeniería y la astronomía para el estudio de fenómenos naturales y la resolución de problemas prácticos.
El legado de Pitágoras en la geometría
El legado de Pitágoras en la geometría es de suma importancia y ha dejado una huella indeleble en el desarrollo de esta rama de las matemáticas. Pitágoras, un matemático y filósofo griego, es considerado uno de los padres fundadores de la geometría y sus contribuciones han sido fundamentales para el estudio y comprensión de esta disciplina.
Una de las principales contribuciones de Pitágoras es el famoso teorema de Pitágoras, que establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Este teorema, representado por la ecuación a^2 + b^2 = c^2, es uno de los pilares fundamentales de la geometría y tiene aplicaciones en diversas áreas de las matemáticas y la física.
Además del teorema de Pitágoras, este matemático también realizó importantes avances en la teoría de los números y en la construcción de figuras geométricas. Se le atribuye la demostración de la irracionalidad de la raíz cuadrada de 2, lo que implicó un importante avance en el campo de los números irracionales.
Pitágoras y sus seguidores, conocidos como los pitagóricos, también desarrollaron una serie de propiedades y teoremas relacionados con los triángulos, los polígonos y los poliedros. Estas contribuciones sentaron las bases para el estudio posterior de la geometría euclidiana, desarrollada por el matemático griego Euclides en su obra «Los Elementos».
La geometría pitagórica se caracteriza por su enfoque en la relación entre los números y las formas geométricas. Los pitagóricos creían que los números y las figuras geométricas eran los elementos fundamentales del universo, y que la comprensión de sus propiedades y relaciones revelaría los secretos de la naturaleza y la realidad.
Las aplicaciones prácticas del teorema de Pitágoras: una herramienta fundamental en geometría y trigonometría
Las aplicaciones prácticas del teorema de Pitágoras: una herramienta fundamental en geometría y trigonometría
El teorema de Pitágoras es una de las herramientas fundamentales en geometría y trigonometría, que permite calcular la longitud de un lado de un triángulo rectángulo cuando se conocen las longitudes de los otros dos lados. Este teorema es ampliamente utilizado en diversas aplicaciones prácticas en campos como la arquitectura, la ingeniería, la física y la astronomía.
**Aplicaciones en la arquitectura:**
El teorema de Pitágoras es esencial en la arquitectura para calcular las dimensiones de estructuras y edificios. Por ejemplo, se utiliza para determinar la altura de una escalera en función de la longitud de sus escalones y su inclinación. También se utiliza para calcular la longitud de las diagonales de un cuadrado o de un rectángulo, lo que es útil para asegurar la simetría y estabilidad de las construcciones.
**Aplicaciones en la ingeniería:**
En la ingeniería civil, el teorema de Pitágoras es vital para calcular las distancias horizontales y verticales en la topografía y la cartografía. Además, se utiliza en el diseño de puentes, carreteras y túneles, para determinar las pendientes y las alturas necesarias. También es aplicado en la ingeniería eléctrica, para calcular la longitud de los cables y las distancias entre torres de transmisión.
**Aplicaciones en la física:**
En la física, el teorema de Pitágoras se utiliza para calcular la magnitud de la velocidad resultante de dos velocidades perpendiculares entre sí. También se aplica en la mecánica para calcular distancias recorridas y tiempos de vuelo en trayectorias parabólicas. Además, es utilizado en la óptica para calcular el ángulo de refracción de la luz al pasar de un medio a otro.
**Aplicaciones en la astronomía:**
En astronomía, el teorema de Pitágoras se utiliza para calcular la distancia entre objetos celestes. Por ejemplo, se puede determinar la distancia entre la Tierra y la Luna utilizando la geometría de los triángulos rectángulos formados por la posición de la Luna y la Tierra. Además, se aplica en la determinación de las distancias entre estrellas y galaxias utilizando la trigonometría esférica.
¡Descubre el poder del teorema de Pitágoras en la geometría y sorpréndete con sus increíbles aplicaciones! Ya sabes, ese teorema famosísimo que nos dice que el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de sus catetos. ¡Pero espera, no te duermas todavía! Porque este teorema no solo es útil para calcular las longitudes desconocidas de un triángulo, sino que también tiene un propósito mucho más profundo en el mundo de la geometría. ¿Quieres saber más? ¡Sigue leyendo en IESRibera y descubre cómo este teorema revoluciona nuestra comprensión de las formas y figuras geométricas!