Recta de perfil
Hay mucho para seleccionar, mas tenemos la misión de asistir a facilitar las cosas compartiendo nuestros perfumes favoritos de todos y cada uno de los tiempos, tales como recta de perfil, nariz recta mujer o bien pinzas punta recta. Prepárate, porque estas son las olores que no podemos dejar de rociar. Encontrar una fragancia consiste en familiarizarse con las notas que le agradan, las que le charlan, y elegir las fragancias en consecuencia. Comprar un perfume por Internet puede ser bastante difícil, pero con tantas marcas que evocan de forma deliberada algunos lugares del planeta o que revelan nombres que insinúan la inspiración de una olor, puedes hacerte una gran idea de lo que hay dentro del frasco. No hay sentido tan poderoso y evocador como el fragancia. Las mejores colonias no son solo el toque final perfecto para tu ropa. Asimismo tienen un significado sensible. Las fragancias pueden transmitir un millón de estados anímicos, desde la relajación y el juego hasta la autoridad y el poder. De ahí que es tan importante elegir la colonia masculina o femenina adecuada para usted.
Listado top ventas para Recta de perfil
Navega por esta gama de singulares productos como recta de perfil, lo mejor en el cuidado de tu bienestar. Vamos a ayudarte a encontrar los mejores modelos, a tener la posibilidad de comparar precios y llegar a la mejor opción para tu bienestar.

SPAL 30100400 Ventilador extractor de 16 pulgadas 12 voltios hoja recta de perfil bajo 1074 cfm VA18-AP10/C-41A
- SPAL 30100400 Ventilador extractor de 16 pulgadas, 12 voltios, perfil bajo, hoja recta 1074 cfm VA18-AP10/C-41A
- El mejor ventilador para motocicletas de carreras, ATV, etc. y/o aplicaciones de enfriador de aceite
- Diseñado para cumplir con los requisitos de refrigeración más rigurosos del automóvil
- Estos ventiladores se pueden montar en cualquier radiador con soportes y cubiertas universales
- Alternativa P/N es VA18-AP10/C-41A


KBNIAN 20 PCS Conector de Esquina Ranura en T EU-2020 Perfil de Aluminio en L Soporte de Esquina 90 Grados de Aleación de Zinc Soporte de ángulo de Esquina de Cnector para Perfil de Aluminio - Plata
- 【Durable y antioxidante】: el conector de ranura en ángulo está hecho de material de aleación de zinc de alta calidad, que es fuerte y duradero y se puede utilizar durante mucho tiempo. Y la superficie del producto es un material cromado, que tiene buenas funciones antioxidantes y antioxidantes, lo que mejora enormemente el ciclo de vida del producto.
- 【Diseño de ángulo recto】: El producto tiene un diseño en forma de L de 90 grados. Se utiliza para las juntas en ángulo recto de 90 grados de los perfiles de aluminio industriales con ranura en T estándar europea. Es una conexión oculta. Puede fortalecer las juntas de esquina en ángulo recto de los perfiles de extrusión de aluminio para extender la vida útil de los perfiles de aluminio.
- 【Aplicable a EU-2020】:Los conectores de ranura en ángulo son piezas de fijación especialmente diseñadas para perfiles de aluminio industriales y otra maquinaria industrial.Nuestros productos son adecuados para ranuras de perfil de aluminio EU-2020 de 6 mm. Adecuados para la mayoría de maquinaria y equipos industriales.
- 【Instalación con tornillos】:El conector de ranura de esquina se utiliza para la conexión en ángulo recto de dos perfiles de aluminio industriales. Durante la instalación, solo necesita insertar los dos extremos del producto en las ranuras del perfil de aluminio y luego usar herramientas para apretar los tornillos para completar la instalación. El efecto de refuerzo es significativo.
- 【Perfil de aluminio reforzado】:Los conectores de ranura de esquina que vendemos son piezas de fijación para perfiles de aluminio industrial y otra maquinaria y equipo industrial. Son muy adecuados para puertas y ventanas de aleación de aluminio, impresoras 3D, máquinas de corte por láser y otros equipos mecánicos. Pueden reforzar perfiles de aluminio. Y el juego tiene una gran cantidad de productos básicos que pueden satisfacer sus diversas necesidades.


VENIBO Junta de ducha de repuesto para encajar, 100 cm, 2 unidades, ideal para puertas de cristal rectas de 6/7/8 mm de grosor, junta de ducha, labio de goma
- ✔️ Ajuste universal y recortable: nuestra junta para puerta de ducha es perfecta para todas las cabinas de ducha habituales con un grosor de cristal de 6, 7 y 8 mm y se puede acortar a cualquier longitud fácil y rápida, por ejemplo, con una sierra de puk o un cúter. Ideal para reemplazar la junta de la puerta de tu ducha.
- ✔️Junta de repuesto para enchufar: el intercambio de la junta de ducha también se realiza en pocos minutos sin habilidad artesanal especial. Retira la junta antigua, limpia el cristal, coloca el nuevo labio de sellado en la puerta desde la parte inferior de la puerta. ¡Y listo! No requiere pegamento.
- ✔️ Nunca más vuelvas a lavar los charcos: gracias al perfil especial de impermeabilización, el agua de la ducha se dirige de forma fiable a la ducha y gracias al labio de sellado altamente flexible se detiene de forma segura en sus barreras. Con nuestra junta de repuesto VENIBO, tu suelo del baño se mantiene seco y seguro.
- ✔️Materiales de alta calidad: recibirás 2 juntas para cabinas de ducha en excelente calidad de comercio especializado - duraderas, resistentes a roturas, a la cal, al moho, flexibles, 100% impermeables.
- ✔️Promesa de calidad: hasta 30 días después de la compra recibirá su devolución de dinero sin preguntas y sin problemas. Compra con nosotros completamente sin preocupaciones y sin riesgo


ENT 11661 Fresa de corte recto HW, Mango (C) 8 mm, Diámetro (A) 10 mm, B 25 mm, D 40 mm, L total de 73 mm, con rodamiento de bola de gran tamaño
- El diámetro del mango (C) es de 8 mm, Longitud del mango (D) 40 mm
- El diámetro (A) es de 10 mm, Tiene una anchura de corte (B) de 25 mm
- Este artículo dispone de una longitud total (GL) de 73 mm y además, incluye rodamiento de bola de gran tamaño
- TIene dos canales (Z) y está principalmente compuesto por carburo (HW)
- Fresa de corte reto con dos canales y rodamiento de bola reemplazable, para un acabado limpio. Adecuado para taladrar. Puede ser usado también como fresa para ranurar. Usado para un trabajo con plantilla, cuando la plantilla está bajo el material trabajado. Adecuado para piezas curvadas.


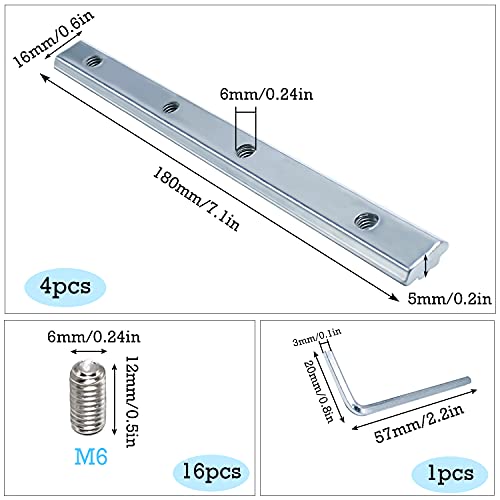
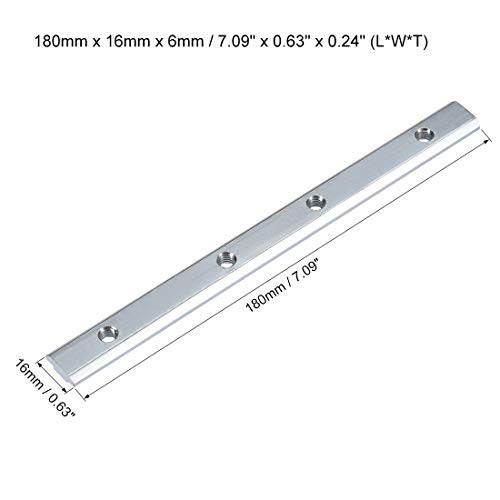
EyPiNS Perfil de Extrusión de Aluminio Recto, 20PCS Conector de Sección 180 mm, Ranura en T, para Conector Hembra de 40 mm Perfil de 8 Perfiles
- [Alta calidad] El conector está hecho de acero al carbono galvanizado. La galvanización hace que el conector sea resistente a la corrosión y el acero al carbono hace que el conector sea más duradero.
- [Tamaño] El tamaño del conector de perfil es de 180 x 19 x 9 mm (largo x ancho x alto) con 4 agujeros de tornillo. El tamaño de los tornillos es M6 x 8 mm (acero inoxidable).
- [Ámbito de aplicación] Este conector de pista se puede utilizar para los perfiles de aluminio de 40 x 40, 40 x 80 y superligeros. Los conectores de pista de la serie EyPiNS 3030 comúnmente utilizados para la construcción de estructuras de marco de aluminio industrial, impresoras 3D, routers CNC, cortadores láser CNC y proyectos robóticos.
- [Fácil de instalar] Este conector de pista sirve para la conexión frontal de dos perfiles de aluminio sin procesamiento de perfiles. Así que puedes conectar fácilmente dos perfiles juntos y extender piezas más cortas.
- [Contenido del paquete] El paquete contiene 20 conectores de perfil de extrusión de aluminio y 80 tornillos M6.


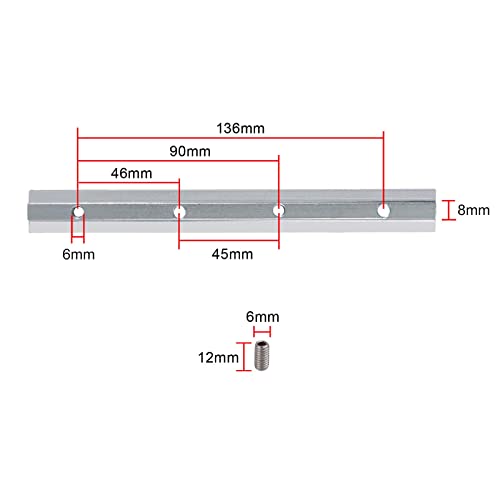
GIAK Conector Recto de Aluminio 4 piezas Conector de Línea Recta 30X30 Ranuras Conector de Perfil 8 Perfiles para Perfil Arquitectónico perfil de Aluminio
Materiales de alta calidad: Conector Recto de Aluminio está hecho de aluminio de alta calidad y los tornillos m6 * 12 están hechos de acero inoxidable 304 de alta calidad, que es duradero, resistente al desgaste y resistente a la corrosión.
Volumen de suministro: En el paquete se incluyen 4 Conectores de Línea Recta y 16 tornillos.
Conexión rápida: Este conector de carril 3030 sirve para la conexión frontal de dos perfiles de aluminio sin procesamiento de perfiles. De este modo, puede conectar fácilmente dos perfiles y extender piezas más cortas.
Áreas de aplicación: Fácil de usar y práctico, este conector se puede utilizar para perfiles de aluminio ultraligeros 30x30, 30x60.
Fácil de instalar: Conector seccional para alineación entre dos perfiles. Se instala en las ranuras de los dos perfiles y se aprietan los tornillos.Viene con una llave para tornillos para una fácil instalación.


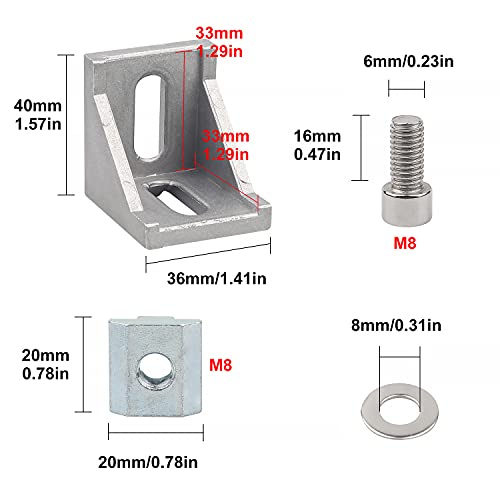
SWAWIS 30 Piezas Soporte de Esquina Forma de L Ángulo Recto, 4040 Perfil de Aluminio Soporte de Ángulo Recto, Soportes de esquina de acero inoxidable
- 【El paquete contiene】 30 x junta de esquina 40x40, 60 x tornillo llave hexagonal M8, 60 x arandela, 60 x tuerca deslizante T M8. Material de montaje Soporte de pared en ángulo Material de montaje para el perfil de aluminio 4040.
- 【Adecuado para】 Perfiles de aluminio, perfiles de pilares, tecnología de conexión y accesorios, ¡Perfecto para conectar perfiles de aluminio con, por ejemplo, material de paneles! Se utiliza sobre todo para el montaje de estructuras industriales de aluminio.
- 【Fácil instalación】 Instalación cómoda, puede fijar fácilmente los conectores con tornillos y tuercas.
- 【Muchas aplicaciones】 El producto tiene una amplia aplicación, se puede utilizar para reforzar los ángulos rectos de la puerta, las ventanas, los muebles, etc.
- 【Servicio al cliente】 365 días para el servicio de devolución sin preocupaciones o la entrega de reemplazo. Si tiene algún problema, le responderemos a su correo electrónico en un plazo de 24 horas.


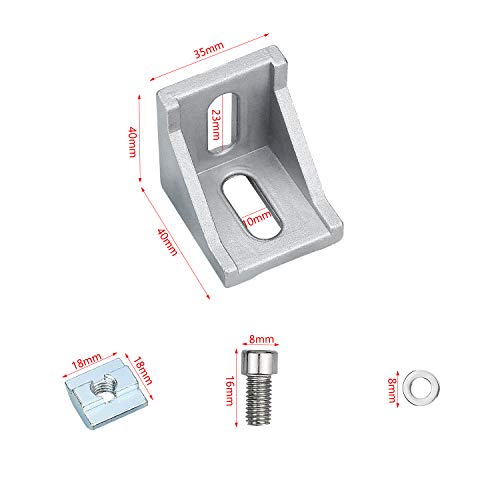
20 Pcs Soporte de Esquina Forma de L Ángulo Recto 4040 Sujetador Hardware Perfil de Aluminio


20 Pcs Soporte de Esquina Forma de L Ángulo Recto 4040 Sujetador Hardware Perfil de Aluminio
- 【Práctico set】 - Pack de 20. 1 paquete contiene: 1 x conector en ángulo 4040, 2 x 8 * 16 tornillos, 2 x 40 * tuercas de martillo M8, 2 x anillos de sellado planos M8.
- 【Material resistente】 - Fabricado en aluminio fundido espesado, resistente, estable, inoxidable y duradero.
- 【Aplicación】 - Se adapta a perfiles de aluminio de 40x40, 40x80, perfiles de puntal, tecnología de conexión y accesorios. Se adapta a la ranura 8.
- 【Buena mano de obra】: no tiene bordes afilados y tiene una superficie lisa.
- 【Fácil de usar】: todo está ahí para lo que necesita instalar.


Topex 01A427 Tijeras corta chapa (250 mm, recta), 250mm
- Cortachapas
- Cabeza cromo-vanadio
- 250mm
- Corte recto


Pedros PIE para JAULAS 60CM
- CARRO


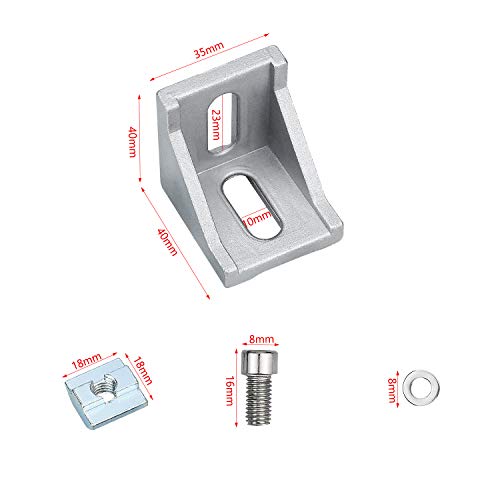
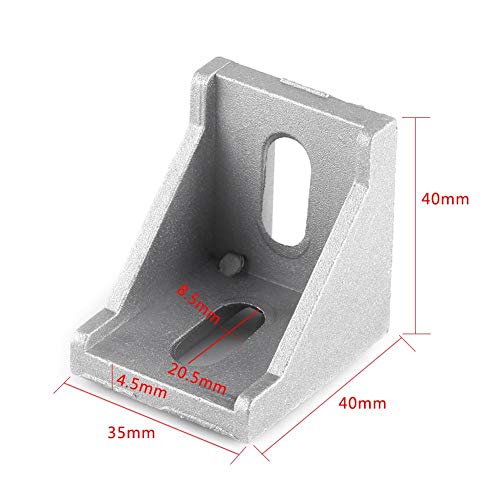
5pcs 4040 Aleación de aluminio en forma de L Escuadra de esquina ángulo recto Soporte de la esquina Sujetador 40x40mmx35mm<br/>
- MATERIAL: Estos tirantes de esquina están hechos de aluminio que son duraderos, sólidos y versátiles, un sujetador perfecto para sus muebles.
- CÓMODO PARA UTILIZAR: Se pueden abrochar simplemente con pernos y tuercas. (los pernos y las tuercas no están incluidos) y con una cubierta protectora en un lado, retírelo antes de la instalación.
- APLICACIÓN ANCHA: Ampliamente utilizado para reforzar las juntas de ángulo de esquina de puertas, ventanas, muebles, etc.
- CONOZCA SU NECESIDAD: Hay un total de 5 piezas de corchetes en un paquete que puede usar para muchos proyectos.
- TAMAÑO DEL SOPORTE: 40 x 40 x 35 mm / 1.57 x 1.57 x 1.37 \


Sourcingmap Conector de línea recta, soporte de junta con tornillos para perfil de extrusión de aluminio
- [Utilizado para] - Perfil de aluminio.
- [Tamaño] - /.
- Material: fabricado con acero al carbono, acabado chapado en zinc, buena resistencia a la corrosión y duradero.
- Fácil de usar: el paquete viene con los tornillos para una fácil instalación. Cuando se instala, se inserta en el pozo de la junta de dos perfiles, y luego se aprieta con tornillos establecidos.
- [Ampliamente utilizado] – Para construir enrutadores CNC, impresoras 3D, cortadores láser CNC, cortadores de plasma CNC, proyectos robóticos, talladores 3D, protectores de máquinas, estaciones de trabajo, etc.


Perfil con ángulo recto, hecho de plástico, 478704
- El material es de plástico y la superficie es de cerezo
- Espesor del material: 1.5 mm
- Longitud: 1000 mm, ancho: 20 mm, altura: 20 mm
- Durable y duradero


tesa TE05086-00000-02 Cinta de Pintor Standard para Perfiles Rectos, Amarillo, 50mx25mm
- Más que una cinta adhesiva
- Producto de la marca Tesa
- Diseño moderno y funcional

Imágenes de Recta de perfil
Aquí tienes un montón de fotos de recta de perfil para que te formes una idea y puedas escoger entre todos los modelos de perfume. Haz click con el ratón en en una de las fotos para ver la ficha completa del producto y su costo.