Crema de manos cuantas veces al dia
Un aroma propio debe ser intemporal y llevable, en cualquier situación y a cualquier edad. Pero por supuesto, con tantas olores como crema de manos cuantas veces al dia, cuantas tiendas tiene loewe o cuantas tiendas tiene hugo boss en el mercado, hallar el perfume idóneo para ti puede ser un reto. He visto aun pequeños impresionados por los olores agradables. Si es necesario que elijas el mejor perfume o simplemente vas a la tienda a escoger las fragancias con mejor olor, se convierte en un reto. Hay muchas cosas que vas a ver ante ti, mas tomar la decisión de adquirir una va a ser imposible. Debido a la enorme cantidad de opciones, puede ser abrumador. Cambiamos nuestra colonia prácticamente tanto como cambiamos nuestro vestuario. Quieres asegurarte de que tu olor deje una marca en todos y cada uno de los que te rodean. Sin ser demasiado apabullante. La colonia ha avanzado mucho a lo largo de los años y hay tantas opciones basadas en tus olores favoritos, tu personalidad, la temporada del año e incluso la hora del día en que piensas emplearla.
Listado top ventas para Crema de manos cuantas veces al dia
Queremos que con este grupo de productos puedas encontrar crema de manos cuantas veces al dia al mejor precio y buena calidad para el cuidado y bienestar de tu bienestar. Aquí encontrarás lo mejor para tu salud, teniendo la oportunidad de comparar entre las mejores modelos y marcas del mercado.

Cecotec Robot de Cocina Multifunción Mambo 10090, App, Cuchara MamboMix, Jarra Habana con Revestimiento cerámico, 30 Funciones, Jarra de Acero INOX 3,3l Apta para lavavajillas, Báscula incorporada
- Robot de cocina multifunción con 30 funciones: trocea, pica, licua, tritura, sofríe, muele, pulveriza, ralla, recalienta, bate, yogurtera, monta, emulsiona, mezcla, cocina, remueve, cocina al vapor, escalfa, confita, amasa, cocina a baja temperatura, hierve, mantiene caliente, fermenta, SlowMambo, cocina con precisión grado a grado, cocina al baño maría, cocción lenta, velocidad cero y dispone de función turbo. Disfruta de la App Mambo para Smartphone con recetas ilimitadas.
- Jarra de acero inoxidable de 3,3 litros de alta calidad apta para una limpieza rápida y fácil en el lavavajillas. Su velocidad cero permite cocer y sofreír sin necesidad de poner velocidad, como si de una cazuela o una sartén se tratase. Y, además, con la ventaja de cocinar sin tapa. La innovadora función Sofrito a una temperatura superior cuando desees utilizarla para dorar los alimentos, se consigue con la mayor temperatura y la máxima potencia.
- El sistema inteligente de potencia calorífica oscila de 0 a 10 niveles simulando un fuego tradicional con llama suave, media o fuerte. Evita sobrecalentamiento e impide que los alimentos se peguen o se quemen. Motor con doble engranaje que aprovecha, sin esfuerzo, su rendimiento tanto en altas como en bajas velocidades.
- Movimiento SlowMambo que permite cocinar a baja temperatura lentamente mientras remueve constantemente con la cuchara MamboMix de forma tradicional. Consigue los sabores más intensos.
- Incorpora una vaporera de dos niveles con gran capacidad para poder cocinar al vapor sin límites. El accesorio se ensambla sin la tapa de la jarra para poder cocer al vapor una mayor superficie.


Cecotec Cecomixer Easy - Batidora Amasadora, Movimiento Orbital, Capacidad 3 L, Bol de Acero, 5 Funciones (Amasar, Batir, Mezclar, Montar, Emulsionar), 6 Velocidades, 250 W, Azul
- Batidora amasadora con 5 funciones: amasar, batir, mezclar, montar y emulsionar
- Posee 3 litros de capacidad, un bol de acero inoxidable y accesorios para todas sus funciones
- 6 niveles de potencía y movimiento planetario gracias al deslizador del bol que se encuentra en la base, con el que puedes elegir si dejar el bol en posición fija, o darle movimiento orbital
- Diseño de protección en las espirales y varillas que protege la unión con el cuerpo, consiguiendo así que la masa no entre en la parte mecánica y no ocasione ningún problema
- Incorpora un motor reforzado para un perfecto funcionamiento, protegido por el diseño de las varillas y espirales; además, posee un sistema de seguridad que protege al motor de sobrecalentamientos; el security motor system provoca la interrupción del proceso cuando el motor alcanza elevadas temperaturas y solo permite su puesta en funcionamiento una vez se ha enfriado
- Componentes incluidos: Varilla batidora, Varilla amasadora, Cuenco de acero inoxidable


33 cm Hecha a mano Marron elegante Vintage Bolso de cuero del mensajero cada día Bolso de hombro cartera para tablets, ipad, charger perfecta para viaje y oficina regalo para hombres mujeres bolsa de
- De alta calidad. Vintage pero muy elegante 100% piel auténtica messeneger bolsa de ordenador portátil para su computadora portátil de valor.
- El bolso es: 25 cm x 33 cm x 10 cm (altura, anchura, profundidad) que puede muy bien para un ordenador portátil de 33 cm
- La bolsa dispone de tres compartimentos interiores, compartimento del medio bien acolchada para garantizar la seguridad de la computadora portátil. En en el interior, un gran bolsillo con cremallera para mantener los documentos, etc. El Bolso es lo suficientemente grande para acomodar un portátil y algunos libros con cargador, etc.
- Hay un bolsillo en el frontal exterior que fácilmente puede contener pasaporte, teléfono, pequeño bloc de notas, etc. La parte trasera tiene una cremallera pockert para acceder a la bolsa sin tener que abrir la bolsa. El cierre principal es del auténtico hebillas que están a su utilización muy fácil de hacer funcionar una vez que obtiene en una semana o so.
- La bolsa dispone de una amplia correa de hombro ajustable. La correa es lo suficientemente grande para comfartably transportar la bolsa incluso pesado.


Loctite Super Glue-3 Pincel, pegamento transparente con pincel aplicador, adhesivo universal de triple resistencia, con fuerza instantánea y de fácil uso, 1x5 g
- Aplicación con pincel – Loctite Super Glue-3 Pincel es un pegamento líquido de fácil uso, antigoteo, limpio y seguro. Las superficies a pegar deben estar limpias y secas
- Transparente, rápido y multimaterial – Este pegamento rápido se seca en 3 segundos. Sirve para metal, porcelana, plástico*, madera, caucho, mármol y cuero*
- Bote estable – Este adhesivo multiusos es fácil de usar gracias al bote estable y al tapón de fácil apertura. Debe guardarse en vertical y en un lugar fresco y seco
- Triple resistencia – La nueva fórmula del adhesivo impermeable es resistente al agua y al lavavajillas, a los impactos y a temperaturas extremas (de -50 ºC a 120 ºC)
- Envío y detalles – Loctite Super Glue-3 Pincel, tubo de pegamento universal líquido, con nueva fórmula de etilcianoacrilato, transparente, 1x5 g bote, n.º artículo: 2343743


Cantu Gel De Rizos 365 g
- Proporciona brillo brillante y sujeción perfecta para los estilos que quedan
- Reduce el volumen del cabello al alargar los rizos mientras proporciona un agarre duradero
- Libre de sulfatos, siliconas, parabenos o aceite mineral
- Hace los rizos más secos definidos y sanos


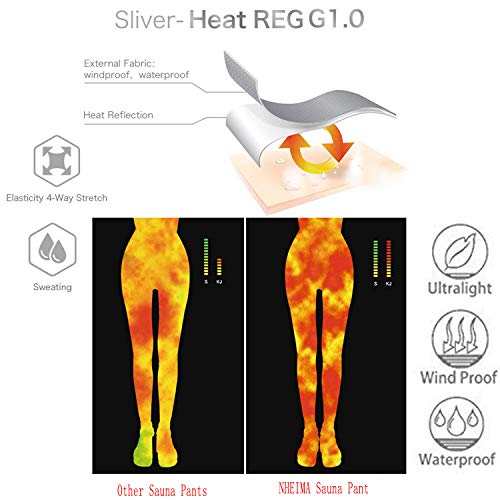
NHEIMA Pantalones de Sauna Adelgazantes Mujer NANOTECNOLOGÍA, Leggins Reductores Adelgazantes, Leggins Anticeluliticos Cintura Alta, Mallas Fitness Push Up para Deporte Running Yoga Gym (S, Black03)
- ►SUDAR HASTA 6 VECES MÁS & QUEMAR EL DOBLE DE GRASA: aumenta la temperatura corporal en la zona abdominal, estimulando la sudoración, expulsando el agua y las toxinas. Casi sin darte cuenta habrás perdido varias tallas en poco tiempo. Ya sea en casa realizando las tareas del hogar, paseando o haciendo ejercicio. Tan solo tendrás que ponértela para empezar a notar sus efectos: aplanas el vientre, modelas la cintura, tonifica los músculos, endurece los glúteos y muslos
- ►FABRICADA CON MATERIAL DE NANOTECNOLOGÍA: diseñados con Nano-plata 9500, el nuevo tejido ultradelgado ofrece un mayor rendimiento térmico y ayudándote a sudar hasta 6 veces más. Aplica esta eficiencia térmica sobre la piel, favoreciendo la disolución de los cúmulos grasos. Además, leggins reductores adelgazantes NHEIMA a diferencia de los trajes de sauna de neopreno generales, NHEIMA NO deja un olor desagradable
- ►DISEÑO ERGONÓMICO Y CÓMODO: pantalones mujer adelgazantes de cintura alta que te permite quemar mas calorías. A diferencia de las medias o los pantalones cortos de sudoración, el leggins anticeluliticos mujer fitness es lo suficientemente largo (hasta los tobillos) para una cobertura perfecta y un tratamiento selectivo de piernas y gemelos. Además, son muy cómodas, ya que permiten libertad de movimientos, ¡Estoy seguro que usted tendrá gusto de él!
- ►MOLDEAR CUERPO & APLANAR VIENTRE AL INSTANTE: gracias a su diseño, te permite moldear toda la silueta, sin que te salgan los antiestéticos michelines, ya que su diseño va desde el abdomen hasta el tobillo. Los efectos que consigues son: reducir las medidas instantáneamente, aplanar el abdomen, reducir la cintura, delinear las caderas y los muslos, esconder la celulitis y estilizar la figura. Los resultados son increíbles mientras se lleva puesta
- ►IMFORMACIÓN DE TAMAÑA OPCIONAL: la información de tamaño exacto de este Control está en la imagen. Por favor NO haga su pedido de acuerdo con la tabla de tallas ofrecida por Amazon - Puedes llevar este mallas mujer fitness push up para correr, pasear, montar en bicicleta, patinar, ir al gimnasio, caminando con el bebe, deporte, yoga, running, ejercicios o para un uso diario


Grande 100ml. Bio Crema de Baba Caracol. Hidratante facial con Ácido Hialurónico y Vitamin C. 20+ Ingredientes Antiedad y Antiarrugas para la cara y Contorno de Ojos. Crema de Dia/Noche y Mujer/Hombre
- ✅ RICA EN PRINCIPIOS BIOACTIVOS: Crema de baba de caracol con ingredientes con efecto antiarrugas que incluye alantoína, ácido hialurónico, vitaminas B1, B2, C, E, rosa de Damasco orgánica, ácido glicólico, elastina, colágeno, betacaroteno, aceite de aguacate, y proteínas y aminoácidos útiles para regenerar la piel.
- ✅ BENEFICIOS PARA TU BELLEZA: el colágeno de nuestra crema hidrata y nutre; el ácido glicólico estimula la formación de colágeno, haciendo que la piel quede iluminada, mientras que las vitaminas y proteínas promueven la oxigenación de la piel, asegurando su hidratación y realizando un efecto antioxidante, cicatrizante y antiedad.
- ✅ EFICAZ EN PIELES DE TODO TIPO Y EDAD: los ingredients activos de nuestra crema reducen visiblemente las líneas finas, las arrugas, los signos del acné, las cicatrices, las rojeces, las manchas y las estrías de la piel, hidratando, nutriendo, regenerando la piel y, al mismo tiempo, disminuyendo sus imperfecciones. Adecuada para ambos sexos.
- ✅ ESTUDIOS A NIVEL MUNDIAL PRUEBAN SU EFICACIA CIENTÍFICAMENTE: enriquecida con extracto orgánico de bayas de Goji: uno de los ingredientes más nutritivos de la naturaleza por su excepcional contenido en vitamina C, los ingredients de nuestra crema ralentizan el proceso del envejecimiento, dejando la piel tonificada, flexible e hidratada y un cutis impecable.
- ✅ HECHA EN ITALIA 100% con CERTIFICACIÓN DE COSMÉTICO BIO ECO (AIAB): Baba producida exclusivamente en granjas italianas y extraída de forma ética y responsable sin que los caracoles sean sometidos a ningún tipo de maltrato. GARANTÍA DEL FABRICANTE - Quedas satisfecho o te lo reembolsamos.


Bella Aurora Doble Fuerza Crema De Belleza Mate Para Piel Mixta - 30 ml.
- Aclara la piel
- Ilumina la piel
- Ideal para piel mixta-grasa


Lictin Almohadillas de Lactancia Bambú Orgánicos para Pérdida de Leche, Bolsa de Lavandería y de Organizadores, 12 Piezas
- Lavar a mano o a máquina con agua fría a 45 °C, no se puede planchar, diámetro de tamaño: 12 cm.
- Los cojines lavables se pueden lavar en la mayoría de lavadoras y luego reutilizarlos, por lo tanto, te ahorrarás dinero en comparación con
- Los productos desechables que le cuestan mucho dinero durante meses, además actúan de forma sostenible y ecológica.
- Discos de lactancia extrasuaves y transpirables de bambú que absorbe la humedad hasta 3 veces mejor que el algodón, garantiza que no penetre la leche en tu ropa, no daña los pezones ni los pechos.
- Seguro, no tóxico, la seguridad de usted y su bebé es muy importante para nosotros, los insertos de bambú de lactancia son la mejor protección posible y discreta para las madres lactantes
- Incluye 1 red de lavandería y 1 bolsa para guardarla, la práctica red para lavar, secar y guardar cómodamente.

Mavala Científico K+ Endurecedor de Uñas Tratamiento para Evitar que las Uñas se Rompan o se Separen, 5 ml
- Mavala científico k+ endurece la uña gracias al ingrediente científico activo que mejora la cohesión de las fibras de queratina permitiendo que las tres capas principales de la uña se unan.
- La punta de la uña es la parte más frágil y desprotegida, que se rompe con facilidad; es por lo tanto la parte de la uña que debe fortalecerse.
- Esta solución acuosa penetrante, que no es ni base ni esmalte, endurece las uñas blandas y evita que se rompan o se separen.
- También contiene lágrimas de resina de cristal, una goma extraída del árbol del pistacho que ayuda al proceso natural de queratinización de las uñas, reforzándolas.
- Utilízalo dos o tres veces por semana hasta haber obtenido los resultados deseados; luego, puedes espaciar las aplicaciones.


Garnier Niños Sensitive Advanced - Protector Solar para Pieles Claras, Sensibles e Intolerantes al Sol, IP50+ - 50 ml (Formato Viaje)
- Muy alta protección solar para niños de rápida absorción contra los efectos dañiños de los rayos UVA y UVB
- Resistente al agua: aplicable sobre piel mojada o seca, rápida absorción, resiste 80 minuntos en el agua
- Fórmula hipoalergénica testada bajo control pediátrico
- Gracias a su textura ligera, su aplicación no resulta pegajosa
- Garnier Delial Protector Solar para Niños es adecuado para todo tipo de pieles, incluso las más sensibles


NIVEA MEN Protege & Cuida Spray, desodorante para hombre con máxima protección 48 horas, spray antitranspirante de cuidado masculino, 0% alcohol - pack de 6 x 200 ml
- Máximo cuidado: conl cuidado de NIVEA MEN, este desodorante antitranspirante en spray cuida al máximo tu piel para evitar las irritaciones
- Protección 48 horas: Este desodorante spray se seca rápidamente y protege eficazmente contra el sudor y el olor durante 48 horas para sentirse seguro y cómodo
- Desodorante sin alcohol: El desodorante 48h de NIVEA para hombre contiene 0% alcohol, por lo que su fórmula suave es apta para todo tipo de piel
- Formato spray: Este desodorante masculino viene en un práctico formato spray que deja una sensación refrescante y una fragancia limpia y masculina en la piel
- Contenido del envío: NIVEA MEN Protege & Cuida Spray, desodorante antitranspirante para hombre, pack de 6, 6 x 200 ml, spray


Remescar - Remescar Bolsas y ojeras - Crema para las bolsas de los ojos - Corrector de ojeras - Elimina las bolsas - Tratamiento para las bolsas de los ojos al instante para hombre y mujer
- CLÍNICAMENTE PROBADO PARA REDUCIR LAS BOLSAS PARA LOS OJOS - Diseñado clínicamente para reducir las bolsas para los ojos y las ojeras - El tratamiento ocular fue desarrollado y producido por líderes innovadores del mercado en la industria del cuidado de los ojos
- RESULTADOS INMEDIATOS - Al aplicar una pequeña cantidad de crema de ojos, las bolsas se reducen hasta un 75 %. El efecto de la crema de ojos dura aproximadamente entre 8 y 10 horas. Adecuado para hombre y mujer
- INSTRUCCIONES PASO A PASO - Encontrará un manual al final de la página, incluido también en la caja, que le guiará en la utilización del producto y le proporcionará consejos para sacarle el máximo partido a la crema
- CUÁNTO UTILIZAR - El tamaño de un grano de arroz para una zona cutánea pequeña y 2 granos si la zona es mayor. Menos cantidad no surtirá efecto, mientras que una cantidad mayor no se absorberá por completo y podría causar irritación
- REMESCAR MEDMETICS - Remescar desarrolla soluciones científicas para la piel para mejorar su autoestima. Nuestra gama de productos sanitarios y cosméticos clínicamente probados están diseñados para solucionar problemas dermatológicos

Imágenes de Crema de manos cuantas veces al dia
Si lo que quieres es elegir de forma visual los productos, puedes ver aquí una galería de imágenes de crema de manos cuantas veces al dia. Haz click con el ratón en una de las imágenes y accederás a la compra online de colonia en concreto viendo sus funcionalidades y costo.