Canas soluciones
Conseguir una fragancia perdurable es casi tan bastante difícil como ganar la lotería. Si estás a la caza de una nueva olor que se adapte a tu estilo y que dure un buen tiempo, descubre opciones como canas soluciones, soluciones canas o bien just for men canas. El poder de una fragancia radica en algo más que en su olor. Los mejores perfumes transportan: pueden levantar el ánimo, servir de recordatorio de un ser querido o bien prosperar tenuemente el impacto de un conjunto. Considere en qué momento y dónde va a emplear el aroma. ¿Te llevará de la oficina a una futura hora feliz o bien a una cita una vez que sea seguro hacerlo de nuevo? ¿O bien es para una ocasión especial específica? Quizás prefieras un aroma más atrayente para una cita nocturna, pero una alternativa más refulgente y relajada durante el día o bien en la oficina.
Listado top ventas para Canas soluciones
Navega por esta gama de multiples productos como canas soluciones, lo mejor en el cuidado de tu salud. Si quieres encontrar multitud de opciones para poder comprar lo mejor para tu cuerpo, te encuentras en uno de los mejores sitios web de la red.

Toppik Spray Retoca Raíces Castaño Claro, Cubre de Forma Instantánea las Raíces y las Canas sin Apelmazar el Cabello, 98 ml
- 100% cobertura canas
- Solución tinte
- Solución cabellos teñidos


Objetivo aprobar Matemáticas 2 ESO: Edición 2016 (Castellano - Material Complementario - Objetivo Aprobar) - 9788469611982
- Muy bueno, con algunos ejercicios resueltos.


Radioplayer España
- Nuevo diseño de 'Mis emisoras', más atractivo, para que las encuentres fácilmente
- Notificaciones de los últimos episodios de tus programas favoritos


Muñecos, metáforas y soluciones: Constelaciones Familiares en sesión individual y otros usos terapéuticos: 10 (AMAE)


English Grammar in Use. Fifth edition. Book with Answers and Interactive eBook.


Concédeme un deseo


Just for men Control GX Champú. Reduce las canas gradualmente. Resultado natural. 118 ml
- Champú que elimina las canas gradualmente y proporciona un resultado natural
- Fácil de usar. Tan sencillo como lavarse el pelo
- Lava y revitaliza el cabello. con Aloe vera y Aceite de coco para un cabello fuerte y saludable
- Suave para uso diario
- Usar diariamente hasta conseguir el resultado deseado
- Para el cabello: Normal

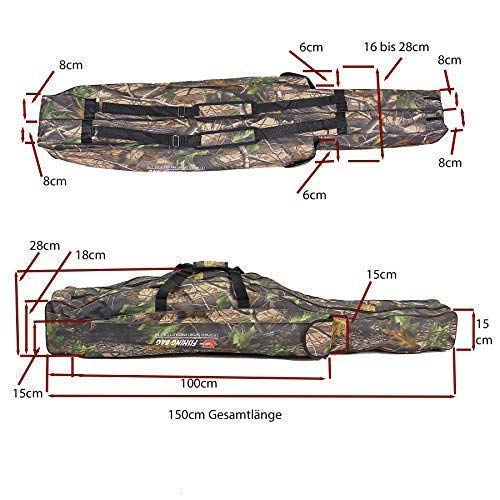
Angel Bolsa de Funda para caña de pescar, Angel Funda caña 150 cm (Tasch e58 W)
- Muy grandes y cualitativa Angel bolsa.
- Dimensiones en total ca Dimensiones: 150 x 16/28 x 15/28/18 cm longitud 150 cm. Ancho 16 hasta 28, Altura 15 hasta 28 'Vea las imágenes'.
- 2 compartimentos largo en la mitte. por 150 cm de longitud, 8 cm ancho, altura 15 cm a 28 cm en el centro. 2 páginas de bolsillos en ambos lados con las dimensiones Dimensiones: 100 x 6 x 15 cm..
- Longitud total: 150 cm. Ancho total si todos los 4 compartimentos plenamente están obstruidos, ca 28 cm altura total 15 cm a la página y 28 en la centro y 18 cm en el otro lado.
- Con cualitativo correa para hombros y espalda.


Auricularesn gaming inalámbricos Gaming con Bass 7.1 Surround y Orejeras de metal auriculares con microfono para PS4, Nintendo Switch ,PC
- Se usa las almohadillas blandas de proteína con alta elasticidad para orejas, no siente dolor con ellas, no tienen presión para orejas, puede utilizarlos durante largo tiempo.
- Transmisión inalámbrica de 2,4G, la velocidad de transmisión es más rápida que Bluetooth, puede lograr una calidad de sonido de HI-FI sin pérdidas.
- El diseño de circuito de energías bajas, la capacidad de batería es más grande, puede trabajar más de 6 horas continuamuente.
- Es compatible con varios equipos, apoya PS4,Nintendo switch,PC y etc.
- garantía de un año

![Rammstein [Vinilo] Rammstein [Vinilo]](https://www.iesribera.es/pics/2020/09/29/rammstein-vinilo-81326.jpg)
Rammstein [Vinilo]


You can do

![Pack True Blood Temporada 1-7 [DVD] Pack True Blood Temporada 1-7 [DVD]](https://www.iesribera.es/pics/2020/09/29/pack-true-blood-temporada-1-7-dvd-81324.jpg)
Pack True Blood Temporada 1-7 [DVD]
- Precio mínimo ofrecido por este vendedor en los 30 días anteriores a la oferta: 55.99€


La bruja (Los crímenes de Fjällbacka nº 10)


Miel de caña 300 grs
- Concentrado del jugo de la caña de azúcar tradicionalmente conocido por "miel de caña"
- Es un alimento muy completo y rico en principios nutritivos fácilmente asimilables como la glucosa, sacarosa, proteínas, sales cálcicas, sales férricas, vitamina B y otros minerales
- Es un delicioso postre. Puede tomarse con queso blando, tostadas, frituras, frutas ácidas, flanes, yogures, refrescos, batidos, etc.
- En la repostería industrial se utiliza para darle más jugosidad y finura a la masa así como un sabor de novedad gastronómica
- En la repostería casera se utiliza para hacer: arropía, torrijas, bizcochos, tortas, maíz acaramelado, batatillas con miel, borrachuelos, flor de piñonate, almendrado, galletas, etc.


Podemos Solucionarlo (We Can Work It Out)


Plex: Stream Movies, Shows, Live TV, Music, and More
- Stream thousands of FREE movies and TV shows from filmmakers around the world with big hits from Crackle, Warner Brothers, MGM, Lionsgate and more! Enjoy everything from Oscar award-winning movies to anime, documentaries, family-friendly shows, and much, much more.
- Watch 80+ channels of free live programming—instantly. From food to news to sports to kids to international content, there's something for the whole family.
- Magically organize all your personal media—photos, music, movies, shows, even DVR-ed TV—and stream it to any device in a beautiful, simple interface; Plex adds rich descriptions, artwork, and other related information.
- Search for your favorite podcast or discover new ones through personalized recommendations. Plus: 30-second skip, variable speed playback, rich discovery, and full Plex-style support for cross-device playback status (including On Deck, so you can pick back up where you left off on any device).
- Get personalized and trusted video news from over 190 global publishing partners (and growing!), including CBS, Financial Times, Euronews, and top local news sources for over 80% of markets in the US.


Matemáticas II. (Aprender es crecer en conexión) - 9788469812778


L'Oreal Paris Magic Retouch Spray Retoca Raíces Castaño 100 ml
- Tiene pigmentos que se adaptan a cualquier color
- Se lava desde el primer lavado de cabello
- Cobertura óptima para raíces y canas

Imágenes de Canas soluciones
Si lo que quieres es elegir de forma visual los artículos, aquí puedes observar una serie de fotos de canas soluciones. Haz click en una de las fotografías y accederás a la obtención online de colonia en concreto viendo sus funcionalidades y costo.






























![Rammstein [Vinilo] Rammstein [Vinilo]](https://www.iesribera.es/pics/2020/09/29/rammstein-vinilo-81326-2.jpg)

![Pack True Blood Temporada 1-7 [DVD] Pack True Blood Temporada 1-7 [DVD]](https://www.iesribera.es/pics/2020/09/29/pack-true-blood-temporada-1-7-dvd-81324-2.jpg)