Moda en matematicas
¿Puedes decir la diferencia entre los perfumes asequibles y los caros? Referencias como moda en matematicas, edps matematicas o alta moda, elegidos por especialistas, pueden olisquear como si costasen un buen dinero, pero todos son sorprendentemente accesibles. La mejor colonia para hombres o mujeres ha de ser esmeradamente emparejada con las situaciones y ocasiones específicas en las que se empleará. Los seductores aromas oscuros, de tabaco y madera se amoldan a los acontecimientos nocturnos, mientras que las olores más frescas o bien cítricas marchan mejor para el uso diario y la oficina. Ya sea que se trate de fragancias florales, perfumes picantes, acordes de oud, o aromas dulces que le agraden, o que le guste la última y más grande fragancia en marcha o que sea un entusiasta de los viejos clásicos, hemos reunido los mejores perfumes de todos y cada uno de los tiempos para inspirar su busca. No hay de qué.
Listado top ventas para Moda en matematicas
Te facilitamos nuestro listado de artículos dónde podrás encontrar moda en matematicas que cumplan los requisitos de tu cuerpo. Queremos ayudarte a encontrar los mejores modelos, a poder comparar precios y conseguir la mejor opción para tu salud.

Pi A La Mode | Regalo divertido pastel matemático a la mode Camiseta
- ¿Eres un matemático que tiene un diente dulce? ¿Te gusta resolver problemas de palabras mientras comes helado? Este arte de día pi a la mode pi es perfecto para ti Es para hombres y mujeres que aman los postres congelados y trabajan como profesor de álgebra y estadísticas.
- Los niños pequeños, niñas, niños y niños pequeños que aman los números pueden utilizar este arte para asistir a una fiesta de cumpleaños temática de helado con familiares y amigos. Puede ser un regalo humorístico de Navidad para tu padre y mamá que son competentes en matemáticas pero tienen diabetes.
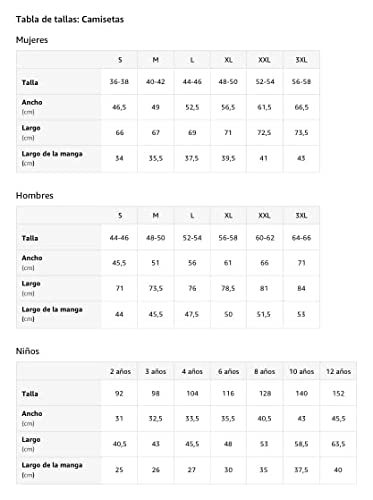
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Matemáticas Moda Matemáticas Profesor Matemáticas Geek Matemáticas Amante Camiseta
- Un hermoso y llamativo atuendo que hace una maravillosa pieza casual para profesores de matemáticas durante todo el año que siempre estará a la moda.
- ¿Pensando en el regalo perfecto de cumpleaños u ocasión especial para tus amigos o seres queridos que son profesores de matemáticas? Sorpréndelos con esta encantadora ropa hoy y hazlos sonreír.
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


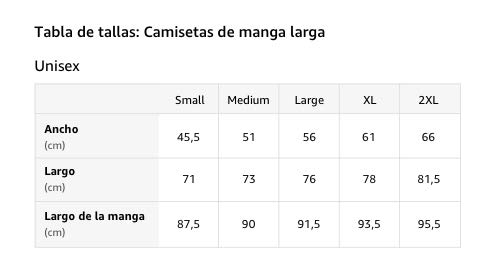
Matemáticas Moda Matemáticas Profesor Matemáticas Geek Matemáticas Amante Manga Larga
- Un hermoso y llamativo atuendo que hace una maravillosa pieza casual para profesores de matemáticas durante todo el año que siempre estará a la moda.
- ¿Pensando en el regalo perfecto de cumpleaños u ocasión especial para tus amigos o seres queridos que son profesores de matemáticas? Sorpréndelos con esta encantadora ropa hoy y hazlos sonreír.
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Dear Algebra T shirt Regalos de matemáticas para hombres Camiseta
- This graphic t-shirt makes a cool outfit or clothes for men, women, kids, boys, girls, youth, teens, dad, mom, mother, grandma, aunt, uncle or granddad. This Tee is also great for Halloween gifts, Birthday gifts, or Christmas gifts. Valentines Day Gifts
- Dear Algebra T shirt Math Gifts for Men Women Kids Teachers
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Ecuación Matemática Fórmula Cuadrática Cool Geek Nerd Regalo Camiseta
- Ecuación Matemática Fórmula Cuadrática Cool Geek Nerd Regalo matemático para los amantes de las matemáticas
- Math Equation Cool Quadratic Formula Geek Nerd Math gift for math lovers
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Monedero La Mejor Profesora De Matematicas del Mundo Regalo Original Profesores Personalizado


La matemáticas es fácil hallar x Aquí es Sudadera
- La matemáticas es fácil hallar x diseño ¡Aquí está el diseño
- Colegio de Educación divertida del profesor de Matemáticas Triángulo humor de la escuela Geometría
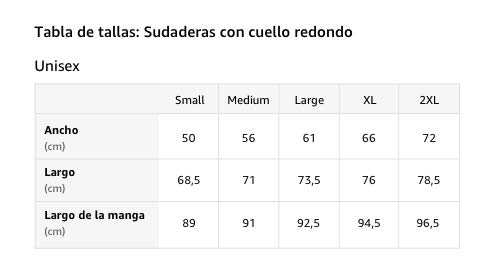
- 241 gr, Encaje clasico, Cinta de sarga en el cuello

Matemático Matemáticas Camiseta
- Avoid negativity f(x)=|x| - evitar la negatividad
- Motivo de juego de palabras de matemáticas, perfecto como una gran idea de regalo para los profesores de matemáticas. También para un estudiante de matemáticas, matemático o ingeniero que es amante de las matemáticas.
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Moda Unisex Divertido Matemáticas Fórmula Analógico Cuarzo Cuero PU Reloj de Pulsera
- Material de la caja: acero inoxidable.
- Estilo: reloj de pulsera.
- Ten en cuenta que debido a los efectos de iluminación, el brillo del monitor, los ajustes de contraste, etc., podría haber algunas ligeras diferencias entre el tono del color de las imágenes y el artículo real.
- Servicio: amamos a nuestros clientes, tu satisfacción es nuestra prioridad, ponte en contacto con nosotros si tienes alguna pregunta, haremos todo lo posible para resolver cualquier problema que encuentres.
- La última tendencia y el diseño especial te ponen en el centro de atención en todas las ocasiones.


QMIN Bolsa de lona con patrón de educación matemática, reutilizable, lavable, bolsa de compras duradera, bolsa de hombro de gran capacidad para mujeres y hombres
- Tamaño: 19.7 x 16.9 pulgadas, correa para el hombro 25.2 pulgadas.
- Material: lona (100% fibra de poliéster), ecológica, duradera, lavable, antiarrugas, no es fácil de romper.
- Estructura: un bolsillo principal, gran capacidad, sin cremallera, se puede utilizar para paraguas, botellas de agua, libros, ropa, zapatos, tabletas, ordenador portátil, iPad y MacBook etc. Hay un pequeño bolsillo con una cremallera, que puede contener teléfonos móviles, tarjetas de autobús, llaves, tarjeta bancaria, cartera, lápiz labial, delineador de ojos y otras cosas pequeñas.
- Diseño: impresión de doble cara, patrones personalizados personalizados, estilo retro, estilo bonito, kawaii, estilo moderno y otros estilos de siembra, unicornio, perezoso, océano, sirena y otros temas, para satisfacer tus diferentes preferencias y necesidades.
- Función: esta bolsa de lona se puede utilizar como bolso de mano, bolso de hombro, bolsa de compras, bolsa de viaje, bolsa de libro escolar; esta bolsa de lona es potente, adecuada para el trabajo, escuela, picnic, senderismo, viajes en el mar, compras en supermercados; esta bolsa de lona también es un gran regalo para la familia, amigos, seres queridos, colegas, compañeros de clase, novias en el día de Acción de Gracias, Navidad, cumpleaños, día de San Valentín.


Mochilas Mujer Casual Escolar Viaje Con Fruta Rosquilla Leopardo Animal Impreso De Estilo Moda Bolso Backpack (FóRmula MatemáTica)
- ✅ Correas de hombro acolchadas ajustables, correas de compresión laterales y correas de embalaje internas.
- ✅ Hecho de lona de alta calidad, moda y durabilidad
- ✅ Incluye muchos bolsillos, proporciona suficiente espacio para sus artículos
- ✅ Fondo reforzado y detalles altos, mayor protección para la mochila
- ✅ [GRANDE] se puede llenar casi todos artículos diarios: tablet/iPad/portátil, libros, estuche, almuerzo, ropa, modedero, paraguas, botella, etc.


Mis Tesoritos 925 Solid Collar Colgante Plata de Ley 925 Chapado en Oro Amarillo Símbolo Matemático Pi (Longitud de Cadena Disponible 40cm - 45cm - 50cm - 55cm)


Matemáticas


Maestro de Juegos de Matemáticas
- caracteristicas:
- - Preguntas que deben ser contestadas rápidamente
- - Dos modos diferentes
- - Tan simple y fácil de usar que lo hace adecuado tanto para niños como para adultos


Vacaciónes Santillana, pensar en matemáticas, 1 ESO - 9788429494440


Geometría y moda: Secretos matemáticos del vestir (Miradas Matemáticas)

Imágenes de Moda en matematicas
Aquí te mostramos un conjunto de fotografías de moda en matematicas para que te formes una idea y puedas seleccionar entre todos los modelos de colonia. Haz click en en una de las imágenes para ver la ficha entera del artículo y su costo.