Aplicacion para saber maquillarse
Hay mucho para elegir, mas tenemos la misión de asistir a facilitar las cosas compartiendo nuestros perfumes preferidos de todos y cada uno de los tiempos, como aplicacion para saber maquillarse, que para maquillarse o pinceles para maquillarse. Prepárate, pues estas son las fragancias que no podemos dejar de rociar. Cambiamos nuestra colonia casi tanto como cambiamos nuestro vestuario. Quieres asegurarte de que tu fragancia deje una marca en todos los que te rodean. Sin ser demasiado apabullante. La colonia ha avanzado mucho a lo largo de los años y hay tantas opciones basadas en tus olores preferidos, tu personalidad, la temporada del año e incluso la hora del día en que piensas utilizarla. ¿Mas de qué forma sabes en qué momento has encontrado la mejor colonia para ti? Vas a reconocer tu aroma propio cuando lo huelas. Es un poco como el amor: Elige la que atraiga más cumplidos. Tú, y la gente que te circunda, deberían disfrutar del aroma.
Listado top ventas para Aplicacion para saber maquillarse
Te facilitamos nuestro listado de artículos dónde podrás encontrar aplicacion para saber maquillarse que se ajusten a los requisitos de tu salud. Encontrarás numerosas referencias de diferentes modelos con buena calidad y con predio competitivo para todo lo que requieres para.

VIVIENNE SABÓ | Máscara de Pestañas Cabaret Volumen Negro | Efecto Panorámico | Cruelty Free | 9ml
- 👁️ Las máscaras de pestañas Cabaret de Vivienne Sabó contiene una fórmula que apora gran volumen, separa cada pestaña y aporta una increíble curvatura mientras las mantiene flexibles y protegidas durante todo el día. Sus agentes hidratantes hacen que nunca tengas la pestaña seca.
- ✨ Rimmel innovador en rendimiento y fórmula con efecto volumen panorámico.
- 🖌️ Goupillón fino de silicona.
- 🌟 Pestañas voluminizadas y divididas al instante, sin grumos.
- 🐹 Producto no testado en animales. Cruelty Free. Hecho en Italia


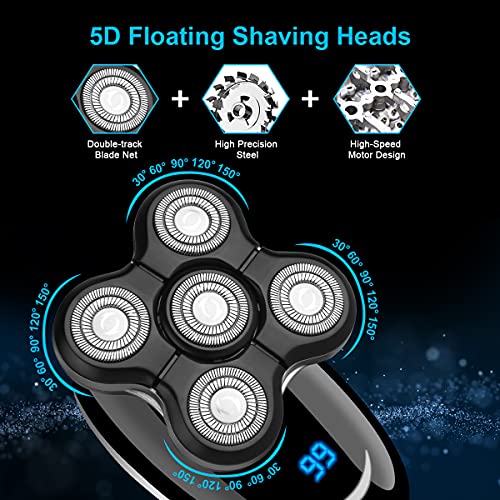
URAQT Afeitadora Eléctrica, 5 en 1 Afeitadora Rotativa para Hombres Impermeable, Afeitadora Barba Hombre en Seco y Húmedo, Maquinilla Afeitar Electrica Hombre con Recortador de Precisión, Negro
- 【AFEITADO APURADO EN SECO Y HÚMEDO】 Con 5 cuchillas independientes, puede adaptarse a los contornos de su rostro, realizar un afeitado apurado sin callejones sin salida y cuidar su piel. Diseño resistente al agua, puede proporcionar afeitado húmedo y seco, puede disfrutar de mejores resultados de afeitado en la ducha.
- 【ACTUALIZACIÓN DE LA FUNCIÓN】 El cabezal de afeitado se puede desmontar como un todo, sin necesidad de abrirlo en varios pasos. Con un almacén de almacenamiento de gran capacidad, la limpieza es más conveniente. La velocidad del producto se actualiza a dos velocidades para elegir libremente. Ligero y portátil, es sin duda el mejor compañero en tu vida diaria.
- 【DISEÑO FLOTANTE GIRATORIO 5D】 El exclusivo diseño de cabezal flotante giratorio aumenta la capacidad de control del afeitado. La red de cuchillos de precisión de alta tecnología y el diseño de doble anillo aumentan el área de contacto en un 50%, se afeitan más rápido, reducen la irritación de la piel y brindan una experiencia de afeitado eficiente y cómoda.
- 【CARGA RÁPIDA】 Solo se tarda 1,5 horas en cargar rápidamente y puede disfrutar de 60 minutos de funcionamiento inalámbrico. La pantalla LED inteligente puede mostrar el porcentaje de energía de la batería, lo cual es conveniente para comprender en tiempo real la capacidad de la batería. El diseño conveniente e inteligente brinda una gran comodidad a su viaje.
- 【KIT DE BELLEZA MULTIFUNCIONAL】 Nuestro kit de cuidado y afeitadora eléctrica tiene 5 accesorios desmontables, que incluyen cortadora de cabello, afeitadora eléctrica, cortadora de pelo de nariz, cepillo de limpieza facial y cepillo de silicona facial para satisfacer todas sus demandas de afeitado facial.


Kit Uñas de Gel, Kastiny 6 Colores Polygel uñas Constructor con Solución Antideslizante, Rosa Desnudo Blanco Marrón Poligel Kit Completo con 100 Uñas Postizas, Decoración/Cepillo/Base/Top Coat
- 【6 Hermosos Colores Desnudos】 Nuestro kit uñas de gel tiene los 6 colores más populares en marrón y rosa nude. Crea manicuras modernas en casa, y estos colores deslumbrantes pero discretos le darán a tus uñas un aspecto encantador que se adapta a cualquier atuendo u ocasión.
- 【Natural y Saludable】 El gel uñas constructor está hecho de ingredientes 100% libres de toxinas, por lo que es seguro, con poco olor, respetuoso con el medio ambiente y no dañará la piel ni el lecho ungueal. ¡Es perfecto para damas elegantes que se preocupan mucho por su salud!
- 【Fácil y Duradero】 El kit de extensión de uñas también incluye la solución de gel, que ayuda a nivelar el polygel y crear una base uniforme. Para obtener resultados duraderos, aplique la capa base y la capa superior, y use las toallitas para uñas para eliminar el aceite y la suciedad.
- 【Kit Gel Uñas Todo en Uno】 6 uñas poligel kit completo (15 g cada tubo), 1 slip solution de 30 ml, 1 base coat de 7,5 ml, 1 top coat brillante de 7,5 ml, 100 tips uñas, 100 diamantes de imitación, pegatinas nail art, lima de uñas, cepillo y clip. Todo lo que necesitas está aquí.
- 【Regalo Ideal y Gran Servicio】 Este polygel uñas viene en una caja muy hermosa y definitivamente es una dulce sorpresa para sus seres queridos. Kastiny se enfoca en ofrecer productos y servicios de calidad. Si tiene alguna pregunta, no dude en comunicarse con nosotros.


Pinkiou Lápices de cejas Marrón, Marrón oscuro, Marrón claro, Negro, Gris, Bolígrafos extraíbles (5 piezas)
- Paquete de 5 colores: negro, gris, marrón, marrón oscuro, marrón claro.
- Duradero: Impermeable, sin floración, natural, se adapta a tus cejas.
- Diseño despegable: no es necesario afilar, es fácil de aplicar y quitar.
- Maquillaje de cejas: ideal para confeccionar definición precisa y efecto espesante.
- Excelente regalo: conveniente para maquillar el color de tus cejas, hacer que te veas naturalmente encantador y elegante.


NYX PROFESSIONAL MAKEUP - Paleta de Sombras de Ojos Cosmic Metals Shadow Palette - Tono 1 Electric Color Multicolor
- Paleta de sombras de ojos que incluye 6 tonos con acabado metálico
- Incluye tonalidades doradas, ciruelas y malvas, inspiradas en nuestros Cosmic Metals Lip Cream
- Acabados suaves y satinados de alta pigmentación
- Combina los diferentes tonos para crear efectos ahumados
- Aplica una pequeña cantidad de cualquier tono encima de un look mate, le aportará un velo metálico sin ser pesado


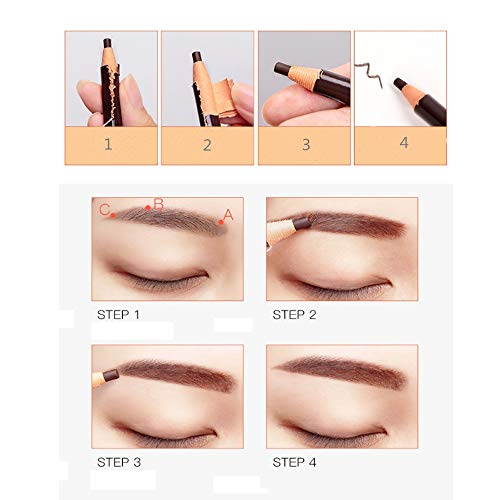
L'Oréal Paris Brow Artist Xpert Liner de Cejas Automático Rellena y Fija 103 Rubio Cálido
- Liner de cejas automático para unas cejas ultra precisas
- Define las cejas con la intensidad que quieras para un look más natural o intenso
- Su formato en pincel y cepillo te permite una aplicación rápida, fácil y precisa
- Dibuja con la punta del liner y rellena con la parte plana según la intensidad
- Su fórmula a prueba de agua ayuda a extender con facilidad el producto y tener unas cejas definidas durante 24 horas


Pintura Corporal y Facial 10ml UV GLOW Conjunto De 6 Tubos Neón Fluorescente incandescente
- Palos de pintura de la cara de excelente calidad.
- Agradable a la piel. Fácil de poner y quitar.
- Más brillante brillo fluorescente bajo luz UV
- Perfecto para todas sus ocasiones especiales y festividades
- Estéticamente certificada


Aceite de baobab Afrinatur · puro · sin refinar · 100% BIO Ecológico Certificado Ecocert · 30 ml
- ✅ Certificación 100% BIO ECOCERT COSMOS ORGANIC
- ✅ Ayuda a restablecer la barrera lipídica y la piel recupera su capacidad protectora frente a agentes externos. Posee un efecto de protección natural frente a los radicales libres y ayuda a la producción de colágeno. Alto contenido en vitaminas A, B, D, E y F. Rico en ácidos grasos insaturados, omega 3 y omega 6.
- ✅ Sin aceites minerales, ni conservantes, ni parafinas, ni parabenos, ni colorantes, ni perfumes sintéticos.
- ✅ Producto cosmético apto para veganos. No testado en animales.
- ✅ Producto recolectado y elaborado por cooperativas de mujeres de África Occidental.


Ardell Paquete De 5 Pestañas Postizas, Demi Wispiesere Con Aplicador De Pestañas De Precisión 1 Unidad 100 g
- Ciglia multipack 5 pack wispies black
- Aplicador de pestañas de precisión
- Ciglia multi pack, 5 pack demi wispies


Marcadores Madera Para Muebles, 17pcs Rotuladores Reparadores para Mobiliario, Reparación de Muebles Pintura y Rayado Reparadores Retoques para Manchas,Rasguños,Piso de madera,Oficina,Cama,Mesa
- El paquete incluye: este kit de 17 piezas incluye 8 marcadores de reparación, 8 barras de cera envueltas en papel y 1 sacapuntas de cera.
- 8 colores únicos: 8 marcadores de retoque grandes con punta de fieltro y 8 crayones de cera para cubrir: arce, roble, cerezo, nogal, caoba, blanco, gris y negro. Puede reparar los muebles usted mismo, no necesita pedir experiencia profesional para retocar sus muebles rayados.
- Calidad Premium: marcadores y barras de cera de alta calidad que cubren rasguños, mellas, rasguños y decoloración en muebles, gabinetes, mesas, camas y más. 100% efectivo y permanente.
- Fácil de usar: retoca dibujando arañazos con marcadores de madera, y deja que se seque rápidamente, ¡mira cómo desaparecen los arañazos ante tus ojos! Estos pueden ser útiles para todo tipo de muebles de madera.
- Preste atención: elija el color más cercano al color de los muebles que desea reparar y pruebe el color en una posición discreta. Apriete la tapa después de su uso.

Sujetadores post mastectomía, pastillas de silicona para levantamiento de senos para mujer, cómodo relleno de silicona para formas de senos, para sujetadores de mastectomía, crossdresser, cosplay
- ▲ Material: silicona médica, material de salud, no daña su cuerpo.
- ▲ Paquete: paquete secreto y sellado, nadie sabe qué hay dentro 100% silicona.
- ▲ Características: tacto suave, se puede estirar, la calidad fuerte no es fácil de rasgar.
- ▲ Ventaja: esay coloreado, puedes maquillarlo; Acepte cambio de tamaño o color y vuelva.
- ▲ Aplicación: puedes usarlo para correr, bailar, dormir, nadar, etc.


Acuaiss Roll-on para Ojos con Ácido Hialurónico y Vitamina B5. Efecto Lifting, Anti Bolsas e Hidrata los Párpados - 15 ml
- HIDRATACIÓN Y ALIVIO - Acuaiss Roll On para párpados contiene ácido hialurónico y vitamina B5 (Dexpantenol) hidrata y repara los párpados y alivia la sensación de tensión y fatiga parpebral
- RELAXING EFFECT - Contorno de ojos de aplicación mediante sistema roll-on que proporciona un efecto calmante, relajante y refrescante de acción inmediata. Suaviza las bolsas debajo de los ojos
- FÓRMULA NO GRASA ANTI ENVEJECIMIENTO - Su fórmula con textura tipo gel está libre de grasas. Acuaiss roll-on combate el envejecimiento de la piel mejorando la elasticidad de los párpados.
- Acuaiss Roll-on está indicado para todas las personas, tanto hombres como mujeres, con sensación de fatiga en los párpados, provocada por: - Llevar mucho tiempo las lentes de contacto puestas - Falta de sueño - Exposición a la contaminación y a ambientes secos - Lectura prolongada - Jet lag
- Aplicar mediante ligeros masajes circulares por toda la zona palpebral. Se recomienda el uso diario del producto, pudiéndose aplicar tantas veces como sea necesario.


Institut Esthederm Intensive Hyaluronic Crema 50 Ml
- Cuidado de la piel :crema facial
- Peso: 50 mililitros
- Crema facial mujer 50 ml


Bourjois Velvet Barra de Labios Líquida Tono 14 Plum Plum Girl - 28 gr.
- Su textura suave y fundente se desliza en los labios y se convierte en un color mate
- Su fórmula sensual proporciona una sensación suave de segunda piel
- La barra de labios es cómoda de usar todo el día
- Con una fórmula enriquecida con aceites evanescentes


Dermacol DC Base Makeup Cover Total | Maquillaje Corrector Waterproof SPF 30 | Cubre Tatuajes, Cicatrices, Acné, Imperfecciones, Manchas en la Piel de la Cara y Cuerpo | Liquido - Mate Natural - 30g
- ✅ TOTAL COBERTURA - ¡Una piel perfecta! Aplique esta base de camuflaje como corrector para los ojos, para manchas en la piel, granos, cicatrices, acné, imperfecciones o incluso un tatuaje.
- ✅ PARA TODO EL DÍA - ¡Quiere un maquillaje de cobertura perfecto que dure! Con nuestra fórmula de larga duración, puede olvidar los retoques y ser una mujer o un hombre irresistible todo el día.
- ✅ EL TONO PERFECTO - Esta base le asegura la piel natural y luminosa que siempre ha soñado, sea cual sea su color de piel. Para pieles muy pálidas o morenas, elige entre nuestros 19 tonos únicos.
- ✅ ¡UN POQUITO BASTA! - Con la aplicación de una cantidad muy pequeña de nuestra crema líquida, puede cubrir un área grande de la piel. Lo sorprenderá la duración de un solo tubo de 30 gramos.
- ✅ HIPOALERGÉNICO, SIN PARABENOS O CONSERVANTES - Nuestro compromiso con su piel va mucho más allá del camuflaje. Para una piel más saludable, nuestra base no contiene productos químicos dañinos.


Erborian- Cc cream Doré scentella - 15 ml
- En una textura fina, ha sido formulado para adaptarse a la piel, para unificar y mejorar el cutis
- Ayuda a brindar brillo, protección e hidratación
- Ayuda a unificar y camuflar las líneas finas de deshidratación y a refinar visiblemente la textura de la piel
- Aplicar como una capa delgada en la cara


Brochas de Maquillaje, 24pcs Maquillaje Profesional Pinceles Maquillaje de Ojos Rubor Contorno de los Labios Corrector Brochas Cosméticas + Bolso Negro
- Este cepillo cosmético muestra su belleza natural y deja un acabado impecable. Cepillos hechos a mano.
- Los materiales de fibra sintética de alta calidad proporcionan un tacto increíble y se sienten cómodos. Adecuado para uso profesional o doméstico.
- Todos los pinceles son extremadamente suaves y fáciles de mantener, perfecto para mujeres de maquillaje y personas con piel normal a sensible, y no irritan. Fácil de usar y portátil.
- Material de alta calidad, cerdas de alta densidad, no se derrame. Los pinceles se sienten suaves y sedosos y son densos y bien formados.
- Suave, pero firme para aplicar maquillaje, las cerdas no se caen al aplicar maquillaje.


Set de brochas de maquillaje profesional Ruesious 10 piezas Pinceles de maquillaje Set Premium Synthetic Foundation Brush Blending Face Powder Blush Concealers Kit de pinceles
- Brochas de maquillaje profesional de mármol – nuestras brochas son utilizadas por artistas profesionales del maquillaje en todo el mundo. Ideal para darte la tranquilidad de que estás utilizando las brochas de maquillaje de alta calidad.
- La mayoría de las brochas de maquillaje sintético no darán a tu piel el tacto suave que te mereces. Es por eso que utilizamos sólo los materiales más premium para asegurar que usted tiene un producto en la palma de su mano que es tan suave como la seda.
- Pinceles de maquillaje con aspecto de mármol blanco. Creemos que cuando usted perfecciona su estilo, usted debe hacerlo con estilo. ¿Qué mejor manera de aplicar su última apariencia que con un juego de brochas de mármol blanco de grado profesional?
- Un cepillo para cada estilo – cuando se trata de elegir el juego de brochas de maquillaje adecuado para usted, el juego de brochas asequibles contiene brochas de maquillaje completas, cepillos de cara (base, polvo, contorno, cepillo de colorete), cepillos de ojos (sombra de ojos, cepillo de cejas).
- Satisfacción garantizada si no te gusta absolutamente tu juego de mármol, háganoslo saber y le daremos un 100% de reembolso o reemplazo.


NYX Professional Makeup Spray fijador Makeup Setting Spray, Larga duración, Ligero, Fórmula vegana, Acabado Matte, 60 ml
- Spray fijador multifunción, Refresca el maquillaje y lo fija durante horas con un suave acabado mate
- Versátil fórmula translúcida, Apto para todo tipo y color de piel
- Dosificador spray fácil de usar, Aplica después de maquillar el rostro, Se recomienda aplicar a 15 cm del rostro de 3 a 5 veces, Deja secar
- Fija la base de maquillaje líquida y en polvo, Reduce la caída del color, Envase compacto fácil de transportar para dar retoques sobre la marcha
- Contenido: 1x NYX Professional Makeup Spray fijador del maquillaje Makeup Setting Spray, Acabado Matte, 60 ml

Imágenes de Aplicacion para saber maquillarse
Si a ti te es más cómodo elegir de forma visual los artículos, aquí puedes observar una galería de fotografías de aplicacion para saber maquillarse. Pincha una de las imágenes y entrarás a la compra online de colonia en concreto viendo sus atributos y valor.