Ejercicios para bolsas y ojeras
Si tienes un presupuesto limitado y deseas encontrar un nuevo aroma propio, puedes estar sosegado sabiendo que estos perfumes económicos no te vaciarán la cartera. Prosigue leyendo y descubre productos como ejercicios para bolsas y ojeras, lo para ojeras y bolsas o bien cosmeticos para ojeras y bolsas y prepárate a fin de que lleguen los cumplidos por tu buena presencia!. El mayor obstáculo para la adquisición de colonias on line es comprar un nuevo aroma antes de olerlo. Para ir sobre seguro, ten una idea de qué notas o bien ingredientes te gustan y cuáles no. Ciertas tiendas darán una tarjeta de muestra o perfumada con la adquisición para probar primero antes de abrir el producto, lo que permite las devoluciones o bien los cambios. Cambiamos nuestra colonia casi tanto como cambiamos nuestro vestuario. Deseas cerciorarte de que tu fragancia deje una marca en todos y cada uno de los que te rodean. Sin ser demasiado abrumador. La colonia ha avanzado mucho durante los años y hay tantas opciones basadas en tus olores favoritos, tu personalidad, la época del año e incluso la hora del día en que piensas usarla.
Listado top ventas para Ejercicios para bolsas y ojeras
Queremos que con este grupo de productos encuentres ejercicios para bolsas y ojeras al mejor precio y mejor calidad para el bienestar y cuidado de tu cuerpo. Si quieres encontrar un montón de opciones para comprar lo mejor para tu cuerpo, te encuentras en uno de los mejores sitios web de la red.

El secreto japonés del yoga facial: Realza la belleza natural de tu rostro y potencia tu bienestar (Salud natural)


Parches para boca APRICOT CON ÁCIDO HIALURÓNICO - 30 usos - ¡Parches antiedad para las arrugas nasolabiales, del labio superior y arrugas de fumadora con eficacia clínicamente testada!
- 'Calidad: Nuestra silicona Boca Pads se fabrican en Alemania y son dermatológicamente probado con "muy bien, vegana y tierversuchsfrei
- Con ácido hialurónico: la boca Pads son enriquecida con ácido hialurónico, trabajando por lo tanto relajantes, contra lluvia y arrugas colágeno producción a
- Efectivo: médico de silicona enriquecida con sustancias activas muy potentes permite efectiva anti arrugas cuidado. probados clinicamente eficacia
- Reutilizable: La única Beauty silikonpads contra exterior labios o nasolabial arrugas un par de boca Pads suficiente para 20 – 30 aplicaciones son lavable y reutilizable.
- Sencilla aplicación: la silicona almohadillas para eficaz anti arrugas piel cuidado regularmente mind. 1 hora posar. resultados visibles después de unos pocos aplicaciones


Fisiocrem Gel Active 250 ml
- Fisiocrem gel active crema 250ml.
- Cuida tu salud de la mano de nuestros productos.
- Cuidarse nunca fue tan fácil gracias a nuestros productos.
- Número de modelo del producto: 8470001533364


Antifaz De Dormir Bluetooth Inalámbrico Masajeador De Ojos Para Aliviar La Presión Y La Hinchazón De Los Ojos Adecuado Para Ojos Secos Ojeras Y Bolsas Debajo De Los Ojos,A
- Elegante, masajeador facial ergonómico, apto para cualquier tipo de cara (hasta 180 grados). Con su banda elástica de larga duración, el dispositivo se puede ajustar de acuerdo con el diámetro de la cabeza, y se puede obtener un dispositivo de masaje con el dispositivo de fuerza-el masaje ocular que se necesita es completamente portátil e inalámbrico. Skanda cabeza masajeador es ideal para la relajación ..
- Eye masajeador-e tiene 4 tipos de masaje: masaje de presión de aire (airbag) / masaje térmica (calor) / masaje de la vibración (vibración masaje) / música de masaje equipada con 5 modos estándar de masaje, modo automático / modo dinámico / modo claro / Sleep modo / airbag modo de calefacción ..
- 2 altavoces incorporados proporcionan una música relajante masaje facial, acompañado de sus canciones-vidrios preferidos tienen memoria interna, puede grabar sus propias canciones en formato MP-3, y relajarse con su control de música favorita volumen y avance / retroceso de la canción. Opciones ..
- Control elegante y fácil de usar panel equipado con un cargador USB para la descarga de canciones y se utiliza como fuente de energía-15 minutos temporizador de función con una bolsa de viaje para un fácil transporte. Este es el mejor regalo para los cumpleaños u otras celebraciones ..
- Servicio de la satisfacción: auricular El sueño viene con 1 año de servicio al cliente y los 365 días de asistencia técnica. Si usted tiene alguna pregunta sobre la máscara para dormir Bluetooth, póngase en contacto con nosotros inmediatamente y le responderemos dentro de las 24 horas. El regalo perfecto para los padres, amantes, amigos, etc. Ya sea en casa, en un hotel o en un avión, es un regalo perfecto para la relajación, la siesta, la meditación, y el insomnio


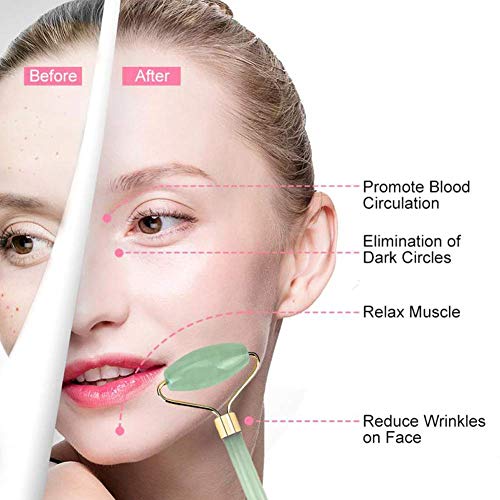
Rodillo De Jade,Rodillo de masaje de jade,Facial Masaje, Masajeador Roller Tools Anti Aging Belleza Natural Dispositivo Herramienta, Para Cuello Cara Ojos Cabeza Cuerpo 2pcs
- 【Jade natural】Las materias primas de las piedras de jade bueno tienen una enorme cantidad de buena energía que tendrá un efecto positivo en su piel. Las mujeres orientales han utilizado Jade para que se vean más jóvenes, se mantengan bellas, para mantener su piel sana y ralentizar el proceso de envejecimiento.
- 【Rodillo de jade】Este rodillo de jade ha sido cuidadosamente diseñado, de doble cabeza, grande y pequeño para satisfacer sus necesidades, es más fácil de maniobrar alrededor de los ojos, la nariz y la boca, así como una cabeza más ancha para áreas de mayor cobertura como la frente , mejillas y cuello Maximice el roll, hold, el masaje facial y la nutrición de la piel.
- 【Piedra Gua Sha】La piedra Gua Sha se puede aplicar con aceite de masaje o crema en la cara, el cuello, la espalda, los brazos y las piernas, luego raspe para masajear o estirar y relajar el músculo.
- 【Rejuvenece y Cura la Piel】Noche de trabajo tardío, ansiedad emocional, líneas finas que lo hacen parecer cansado y aburrido. Después de usar su rodillo de jade a diario, verá una reducción en líneas finas, ojeras e hinchazón de ojos, así como endurecimiento de la cara y apariencia de la piel del cuello revitalizar.Use regularmente todos los días para una mejora notable.
- 【Nota】Cada producto varía de color claro a verde oscuro, translúcido a opaco debido a la naturaleza del jade;Si se rompe durante el envío, no dude en ponerse en contacto con nosotros. Le daremos una respuesta satisfactoria.


Máscara para los ojos, Ojos Parches, Máscara para ojos de colágeno, Parches Hidrogel para Ojos, Con Vitamina C, Reduce las bolsas bajo los ojo, ojeras, patas de gallo e hinchazón - 30 Pares
- 【Caracteristicas】Las máscaras debajo de los ojos son ricas en vitaminas C y colágeno y pueden actuar contra la oxidación y la melanina, reduciendo las ojeras, eliminando la hinchazón, manteniendo la humedad, previniendo y suavizando los ángulos, pueden ayudar a activar la regeneración celular, promover el metabolismo de la piel y reparar la piel. , aclara la piel alrededor de los ojos, mantiene los ojos radiantes y más jóvenes de forma natural.
- 【Humedad natural】La máscara para los ojos se disuelve gradualmente por debajo de la temperatura corporal y penetra rápidamente en la piel, lo que requiere los nutrientes y la humedad para completar la nutrición del ojo. Reduce visiblemente las arrugas y líneas, enfría e hidrata las Vitaminas C, el hialurón y el colágeno.
- 【Cómo utilizar】Lávese los ojos con agua tibia y seque. Quítese la máscara para ojos y cerca de la piel alrededor de los ojos. Quítelo después de unos 15-20 minutos. Retire el parche ocular, masajee la piel del ojo durante 1 minuto.
- 【Hecho de materiales naturales】Mroobest Under Eye Mask está hecho con ingredientes naturales. Lleno de vitamina C, extractos de hialurónico y colágeno. No irrita ni obstruye los poros y es seguro para todo tipo de piel. Las máscaras oculares solubles en agua se pueden disolver completamente en agua tibia sin dejar ninguna contaminación. CONSEJO: solo para uso externo, evite el contacto directo con los ojos, si hay algún inconveniente en la piel, deje de usarlo, mantenga el alcance de los niños.
- 【Usos múltiples y adecuado para todo tipo de piel】Mroobest Vitamin C Under Eye Mask está hecho con ingredientes naturales. No irrita ni obstruye los poros y es seguro para todo tipo de piel. No solo es adecuado para la piel periocular, sino también para decretos, arrugas del cuello, mejillas, mentón y frente. Es perfecto para todo tipo de pieles, incluidas las pieles sensibles, para hombres y mujeres.


Mascara Para Los Ojos, Parches Ojos, Anti Edad Para Oje Ras, Eye Mask, Mascarilla hidratante con ácido hialurónico, Antiarrugas, eliminación de bolsas y ojeras, 60 piezas
- ◆Mejore la opacidad: aclare y aclare, diluya los ojos oscuros, elimine las impurezas acumuladas, elimine las ojeras, resuelva los problemas oculares.
- ◆Levantamiento y reafirmación: hidratante, hidratante, calmante y secante, restaurando la elasticidad de la piel, quitando bolsas debajo de los ojos para que sus ojos se vean más radiantes que nunca.
- ◆Ojos calmantes: alivia la fatiga ocular, la hidratación profunda, refresca el área de los ojos, cuida los ojos y los hace llorosos.
- ◆FÁCIL DE USAR: después de limpiar su cara, saque la máscara para ojos y aplíquela sobre la piel alrededor de los ojos. Espere de 15 a 20 minutos para que se absorba completamente. Retire la máscara para los ojos, masajee suavemente la piel alrededor de los ojos.
- ◆ATENCIÓN: Adecuado para todo tipo de piel, solo para uso externo, evite el contacto directo con los ojos, si tiene problemas con la piel, no lo use, mantenga el alcance de los niños.


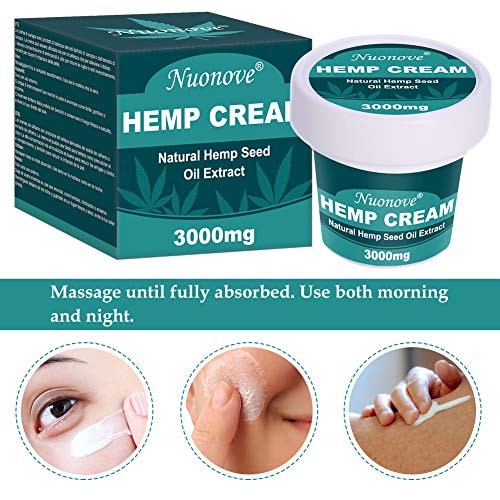
Cannabis Crema, Bálsamo de Cáñamo, Crema de Cáñamo, Antiinflamatorio, Anti-acné, Anti-oxidación, Eliminación de arrugas, Antienvejecimiento, 40 g
- 【Crema de cáñamo 100% natural】 La crema de cáñamo protege contra diferentes factores ambientales y ayuda a reducir la aparición de líneas finas, arrugas, edema, ojeras, bolsas debajo de los ojos, líneas finas y caída debajo y alrededor de los ojos, reduciendo significativamente las patas de gallo La aparición de líneas finas y líneas gruesas y profundas lo hace impecable.
- 【Hidratación intensa】 La crema de cáñamo es profundamente hidratante, hidrata y protege durante 96 horas, restaura la humedad para aliviar la piel seca, haciendo de esta crema de día la crema hidratante perfecta para la cara, calma y calma eficazmente los parches secos, grietas e irritación de la piel.
- 【Antienvejecimiento】 Esta crema de día para antienvejecimiento proporciona la solución antienvejecimiento perfecta con aceite de cáñamo y el poder de refuerzo de colágeno del ácido hialurónico para proporcionar el mejor tratamiento antiarrugas y líneas finas, la crema se puede usar tanto para la belleza como para el dolor aliviar los propósitos.
- 【Relexión y calmante】 Las propiedades antiinflamatorias de la crema de cáñamo hacen que esta crema de día sea excelente para aliviar la tensión, el estrés y la ansiedad. y puede aumentar la sensibilidad de la piel, la elasticidad y mejorar rápidamente la suavidad de la piel, reparar la textura de la piel seca, suelta y envejecida.
- 【Anti-oxidación】 Combate las imperfecciones y los problemas de la piel. Antibacteriano, antibiótico que es un antioxidante fuerte. La crema se puede usar tanto para belleza como para aliviar el dolor.


Máscara para los ojos, Parches para los ojos, Ojos Parches, Máscara para ojos de colágeno, Contorno de Ojos Antiarrugas, Anti edad para ojeras,bolsas,patas de gallo e hinchazón, 60Pcs
- 【Características】Colágeno Golden Eye Mask reduciendo círculos oscuros, eliminando la hinchazón, manteniendo la humedad, previniendo y antienvejeciendo y alisando ángulos, puede ayudar a activar la regeneración celular, promover el metabolismo de la piel y reparar la humedad de la piel, mejorar efectivamente la tensión y elasticidad de la piel del ojo. El refuerzo extra de colágeno regenera el área sensible de tus ojos con un efecto antiarrugas.
- 【Humedad natural】la máscara para los ojos se disuelve gradualmente por debajo de la temperatura corporal y penetra rápidamente en la piel, lo que requiere nutrientes y humedad para completar la nutrición del ojo. Reduce visiblemente las arrugas y líneas, enfría e hidrata el hialuron y el colágeno.
- 【Adecuado para todo tipo de piel】máscara para ojos está hecha con ingredientes 100% naturales. No irritará ni obstruirá los poros y será 100% seguro para todos los tipos de piel. Solo para uso externo, evite el contacto visual directo, si hay algún inconveniente en la piel, deje de usarlo, mantenga el alcance de los niños.
- 【Fácil de usar y conveniente lávese】los ojos con agua tibia y seque. Retire la máscara de ojo y cerca de la piel alrededor de los ojos. Quítelo después de unos 15-20 minutos. Retire el parche del ojo, masajee la piel del ojo por 1 minuto.
- 【El mejor regalo】Día de San Valentín, Acción de Gracias, Navidad o cualquier otra ocasión especial, este es un buen regalo para la familia, el amor o los amigos.


Remescar - Remescar Fórmula Nueva y Mejorada Bolsas y ojeras 2 - Crema para las bolsas de los ojos - Corrector de ojeras - Elimina las bolsas - Tratamiento instantáneo para bolsas de ojos
- CLÍNICAMENTE PROBADO PARA REDUCIR LAS BOLSAS PARA LOS OJOS - Nueva fórmula, más enriquecida con ingredientes innovadores. Diseñado clínicamente para reducir las bolsas para los ojos y las ojeras - El tratamiento ocular fue desarrollado y producido por líderes innovadores del mercado en la industria del cuidado de los ojos
- INSTRUCCIONES PASO A PASO - Encontrará un manual al final de la página, incluido también en la caja, que le guiará en la utilización del producto y le proporcionará consejos para sacarle el máximo partido a la crema
- CUÁNTO UTILIZAR - El tamaño de un grano de arroz para una zona cutánea pequeña y 2 granos si la zona es mayor. Menos cantidad no surtirá efecto, mientras que una cantidad mayor no se absorberá por completo y podría causar irritación
- REMESCAR MEDMETICS - Remescar desarrolla soluciones científicas para la piel para mejorar su autoestima. Nuestra gama de productos sanitarios y cosméticos clínicamente probados están diseñados para solucionar problemas dermatológicos


Bella Aurora Crema Contorno de Ojos Hidratante Anti-ojeras Anti-fatiga, Reduce Bolsas, Manchas y Atenúa las Arrugas, 20 ml
- Tratamiento del contorno de ojos anti-ojeras y anti-fatiga. Ideal para tratar los problemas específicos del contorno de ojos, rictus y labios.
- Con la combinación de activos ayuda a hidratar intensamente la parte más frágil del rostro, atenuar bolsas y ojeras visibles y a reafirmar el párpado caído, dando luz y juventud a la mirada.
- Aplicar a toques con el dedo anular (el dedo que menos fuerza tiene) en la zona orbicular justo encima del hueso. El producto cuando penetra, emigra y trata una zona más amplia hasta su completa absorción. También podemos trabajarlo con lisajes en la zona donde se observen líneas de expresión marcadas, y sobre el contorno de labios o rictus. Posteriormente aplicar el tratamiento habitual en todo el rostro.


PRECIO DE LANZAMIENTO Crema Contorno de Ojos Lifting ORGÁNICA para Bolsas y Ojeras 30ml – Crema Antiarrugas con Acido Hialuronico, Aloe Vera Puro y Aceite de Argán – Belleza para Mujer de Alemania
- ✅ CREMA DE OJOS LIFTING ANTIARRUGAS ANTIOJERAS DE CALIDAD ORGÁNICA / PARA UNOS OJOS BONITOS Y RADIANTES: ¡Por fin! Llegó la crema orgánica para ojos de Satin Naturel. Como siempre vegano, orgánico y hecho en Alemania solo con los mejores ingredientes y mucho amor. Nuestra crema para el contorno de ojos, bolsas, ojeras y ojos hinchados combina las valiosas propiedades del acido hialuronico, la manteca de cacao, el aceite de argán y la vitamina E. Dile adiós a las bolsas y a las ojeras.
- ✅ BASE DE ALOE VERA ORGÁNICA ÚNICA EN SU CLASE: en vez de utilizar el agua, que es ineficaz, como ingrediente principal (como otras empresas), utilizamos aloe vera orgánico que aporta un componente profundamente nutritivo e hidratante al producto. La rica manteca de cacao orgánica le da a la piel una sensación suave duradera. El aceite de argán orgánico y el ácido hialurónico añaden un efecto antienvejecimiento. Utilizamos frascos de vidrio violeta para proteger los valiosos ingredientes.
- ✅ ¿QUÉ PUEDE HACER NUESTRA CREMA POR TI?: actúa eficazmente contra las ojeras, arrugas y líneas finas; protege contra los radicales libres (propiedades antioxidantes); aporta hidratación a la piel. La crema facial antiarrugas rellena el contorno de los ojos y crea una firmeza visible en cuestión de semanas. Reduce las arrugas, suaviza las líneas finas y minimiza las bolsas y ojeras. Para unos ojos bonitos, radiantes y rejuvenecidos.
- ✅ COSMÉTICA NATURAL ORGÁNICA VEGANA / CREMA ANTIARRUGAS HECHA EN ALEMANIA: las pruebas dermatológicas confirman que nuestra crema antiarrugas y antiojeras es suave para la piel. La compatibilidad con la piel es importante, especialmente en el área sensible alrededor de los ojos. Nuestra crema se ha formulado específicamente para esa zona, por eso no contiene aceites esenciales y es casi inodoro. Además, se fabrica en Alemania SIN parabenos, sulfatos, microplásticos ni crueldad animal.
- ✅ NUEVO: COMPRA 1 PRODUCTO. PLANTA 1 ÁRBOL. OBTÉN RESULTADOS o recupera tu dinero: impulsados por tu satisfacción, nos esforzamos por ofrecerte excelentes productos. Lo verás en nuestros ingredientes efectivos de primera calidad, altos estándares de calidad y en nuestra excelente atención al cliente. Si, aun así, no estás satisfecho, contáctanos antes de 30 días desde tu compra y te devolveremos tu dinero. Quiérete a ti y a nuestro planeta. ¡Elige Satin Naturel!

Imágenes de Ejercicios para bolsas y ojeras
Si para ti es más cómodo elegir de forma visual los artículos, puedes observar aquí un conjunto de fotos de ejercicios para bolsas y ojeras. Haz click con el ratón en una de las fotografías y entrarás a la compra online de colonia en concreto viendo sus propiedades y precio.