Patron vestido novia
Existen muchos perfumes en el mercado y en cualquier tienda de venta al público on-line. No obstante, no se puede estar seguro de su longevidad y calidad. Dale una ocasión a referencias tales como patron vestido novia, vestido dior o vestido elie saab y ya verás como olerás mucho mejor!. Las colonias de en la actualidad no tienen un propósito tan puramente práctico, mas sí uno más interesante: asistir a tener suerte. Si se combina el aroma adecuado con el hombre y mujer adecuados, se genera algún tipo de brujería. La colonia es el arma secreta de todo hombre y mujer. Un spray antes del trabajo, de una cita o de una fiesta no sólo proporciona un impulso instantáneo en el atrayente, sino que también infunde una confianza extra cuando se lleva en compañía de otros. ¿De qué manera hace el caballero o bien la dama modernos para comprar la mejor colonia? Comienzan por educarse en la ciencia de los aromas.
Listado top ventas para Patron vestido novia
Esperamos que con este listado de productos encuentres patron vestido novia al mejor precio y buena calidad para el bienestar y cuidado de tu cuerpo. Te aseguramos que llegarás a encontrar las mejores opciones y precios de todo lo que estés buscado para tu salud, dándote la oportunidad de descubrir varias modelos y marcas.

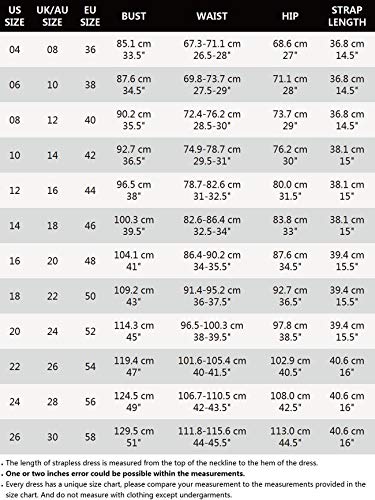
Ever-Pretty Asimétrico Vestido de Novia para Boda Largo para Mujer Sencillo Escote en V de Tirante Encaje Volantes Negro 36
- Confíe en la guía de tallas en las fotos, en lugar de su tamaño habitual
- Embalaje: nuestros vestidos están doblados para un envío más rápido. Utilice vapor para eliminar las arrugas a su llegada.
- Cierre: Se oculta una cremallera en la espalda. Ropa interior: No está acolchada, con forro. Estiramiento: la tela no se estira.
- Diseño: este vestido de novia blanco está diseñado con tirantes ajustables con cuello en V y utiliza el popular encaje bordado y costuras irregulares en el dobladillo con patrón de hoja de loto, elegante y romántico. No es perfecto para bodas, también es adecuado para vestidos de noche, vestidos de fiesta y puede usarlo para cualquier evento formal.
- Ocasión adecuada para la noche, cóctel, fiesta de graduación, ocasión formal, regreso a casa, invitado a la boda, graduación, ceremonia, banquete, dama de honor, compromiso, baile, ocasión especial, fiesta


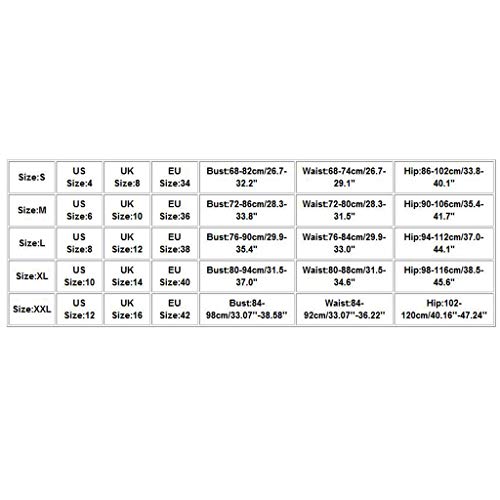
Bañador Efecto Vientre Plano, Bikinis Juveniles 2022, Patron Bañador Mujer, Vestidos De Novias para La Playa, Bikinis Madre E Hija, Vestidos De Novia para Bodas En La Playa, Bañador Leopardo Mujer
- 【Entrega Rápida】 7-21 días. Se recomienda un tamaño más grande. Para elegir una logística más rápida para usted. Trajes de baño para mujer : algodón / spandex / poliéster. El material cómoda no te da comezón, pero pone tu cuerpo en un estado relajado. Tejido elástico, liviano, que suelta perfectamente la forma de su cuerpo, suave, transpirable, de alto rendimiento, suave y elástico que proporciona una absorción de humedad excepcional, mantiene la piel seca y cómoda, te gustará.
- moda baño mujer, sujetador bikini, bañador pantalon mujer, bikini volantes mujer, bañador reductor barriga, bañador brasileño mujer, bikinis reductores tallas grandes, bañador vestido, bañadores, pareos playa mujer, marcas de bañadores mujer, bikinis de talle alto, bañadores mujer 2022, mejores bikinis 2022, bikini rosa fluor, bikinis y bañadores 2022, bañadores con aros, bañadores con falda, bikinis push up 2022, tunicas playeras, bikini brasileño alto, bañadores push up
- pareos mujer playa, bikini mujer, bikinis rebajas, mujeres en bikini, bikinis 2022, bikinis corte v, bañadores transparentes mujer, bañador mujer pantalon corto, bañadores de chicas, camiseta playa mujer, bañadores talle alto, bañadores tankini, bikinis altos cintura, mujeres mini bikini, bañadores de rayas mujer, bañadores mujer gorditas, vestido playero talla grande, tunica mujer playa, vestidos de novias de playa, bikini para chicas, bañadores una pieza mujer, chica en mini bikini
- bañadores, bikinis, bikinis de mujeres, bikinis para poco pecho 2022, bañador amarillo mujer, los mejores bikinis 2022, bañadores mujer rebajas, bikini tiro alto brasileño, bikinis bonitos mujer, bikini short mujer, bañadores natacion mujer con sujetador, bañador waterpolo, bikinis mujer baratos, bikini surf mujer, bikinis bonitos 2022, bañador para gorditas, bañador verde mujer, bikinis tallas grandes pecho, vestido camisero playa, bikini push up mujer
- bikinis rebajas, tankini reductor, braguita bikini talle alto, bañador leopardo mujer, bañadores mujer push up, braguita bikini azul marino, bañadores de mujer reductores, bañadores mujer con relleno, bikinis madre e hija, bañador efecto vientre plano, bañadores con falda tallas grandes, patron bañador mujer, bañador faja mujer, bañador espalda descubierta, bañador largo mujer, bikini de aro, mujeres bikinis brasileños, bikini copa grande, bañador vestido mujer, bañador camiseta mujer


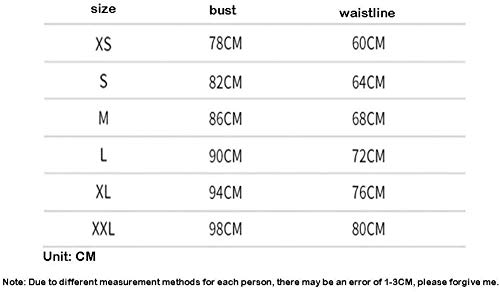
Bikini Negro Mujer, Bikinis De Moda 2021, Trajes De Baño Mujer 2021, Mujeres Gordas En Traje De Baños, Bikinis Verano 2021, Vestidos De Novia Playa, Bikini Brasileño Mujer, Traje Baño Ropa Playa Mujer
- 【Entrega Rápida】 7-22 días. Para elegir una logística más rápida para usted. Trajes de baño para mujer : algodón / spandex / poliéster. El material cómoda no te da comezón, pero pone tu cuerpo en un estado relajado. Tejido elástico, liviano, que suelta perfectamente la forma de su cuerpo, suave, transpirable, de alto rendimiento, suave y elástico que proporciona una absorción de humedad excepcional, mantiene la piel seca y cómoda, te gustará.
- 【Bikinis encubrir push-up】 El mejor Trajes de baño para mujer, perfectos para actividades versátiles como natación, deportes, playa, hogar, casual diario, fiesta, correr, ejercicio, fitness o viajar en todas las estaciones. Lindos trajes de baño, adecuados para trotar, caminar, andar en bicicleta, bailar, entrenamiento en el gimnasio o uso diario. El mejor regalo para ustedes, regalos nupciales, esposa, mamá, amigos, novia, amante, los mejores regalos para ella.
- 【Elegante y Encantador】 Los trajes de baño para mujeres para el sexo están disponibles en varios tamaños y colores para su elección. Sorprende a tu amorcito con este sujetador de cobertura total. Encubrimientos de playa traviesos linda el bikinis para Mujer nunca te defraudará. Este conjunto de bikini sexy aumenta tu confianza y sensualidad en ti mismo frente a tu amante, lo que te hará sexy y misteriosa por mostrará curvas sexys como un regalo para tu esposo.
- 【Moda Diseño】 ERLINSHI el traje de baño de talla grande para mujer se adapta a todas las formas del cuerpo y muestra tus senos y glúteos de la mejor manera. Las tapas elásticas con hacer subir muestran muy bueno tus figuras, creando una imagen atractiva y sexy, te hace más elegante y encantador, condimentando tu vida. Nuestro tamaño es asiático. [ Consulte la descripción del artículo a continuación para obtener detalles sobre el tamaño.]
- 【Garantía del 100%】 Todos merecen los mejores regalos. Traje de baño de dos piezas ERLINSHI sin costura, maravilloso regalo para familiares y amigos, disfrutando juntos de los llamativos accesorios. Nuestra máxima prioridad es la satisfacción de los clientes. Si hay algún problema con el producto, no te preocupes, no dude en contactarnos dentro de los 32 días y le daremos un cambio o devolución y un reembolso completo.


Bañador Efecto Vientre Plano, Bikinis Juveniles 2022, Patron Bañador Mujer, Vestidos De Novias para La Playa, Bikinis Madre E Hija, Vestidos De Novia para Bodas En La Playa, Bañador Leopardo Mujer
- 【Entrega Rápida】 7-21 días. Se recomienda un tamaño más grande. Para elegir una logística más rápida para usted. Trajes de baño para mujer : algodón / spandex / poliéster. El material cómoda no te da comezón, pero pone tu cuerpo en un estado relajado. Tejido elástico, liviano, que suelta perfectamente la forma de su cuerpo, suave, transpirable, de alto rendimiento, suave y elástico que proporciona una absorción de humedad excepcional, mantiene la piel seca y cómoda, te gustará.
- bañadores con push up, bikini 2022 mujer, bikini blanco push up, braguita bikini negra, comprar bikini mujer, bikinis 2022 push up, bikinis altos de cintura, braga tanga bikini, bañador escote v, bañadores mujer con aros, bikini talle alto brasileño, mujeres con micro bikini, playa mujer, bikini parte de abajo tiro alto, bañadores adolescentes chicas, bañadores online mujer, bikinis originales 2022, bodas en la playa vestidos, vestido invitada boda playa
- pantalon corto bañador mujer, bikinis talla s, bañador de pantalon mujer, bañador rebajas mujer, mujeres gordita en bikini, bañadores mujer una pieza, trajes de baño de embarazadas, braga bikini alta negra, bikini natación, vestidos de baño para gordita, traje de baño sexys, conjunto bikinis, bikinis con cremallera, boda de playa vestidos, bañadores y tankinis, relleno bañador mujer, bikini brasileño tanga, mujeres con bikini brasileño, bañador mujer verde
- bañador madre e hija, bikinis blancos 2022, bañadores competicion mujer, bañador deportivo mujer, vestido para ir a la playa, vestidos para boda en la playa, trajes de baño para chicas, bañador vientre plano, bikini negro push up, bañadores reductores de barriga, bikini copa a, bañador espalda abierta, bañadores enteros, bañador lunares mujer, bikini tanga mujer, bañador niño natacion, mujeres en traje de bano, bikini rosa palo, bikini top mujer
- bañadores mujer, bañadores bandeau, bikinis juveniles 2022, bikini sin relleno, top bikini mujer, bañadores mujer con falda, bikinis camiseta, mujer en bañador, bikinis de crochet para mujer, vestidos de novias para la playa, vestido transparente playa, bañadores shapewear, bañadores juveniles mujer, bañador talle alto, bikini con pantalon corto, vestidos cortos playa, bañadores xxl mujer, bikinis con camiseta, braga bikini blanco, bañador cremallera mujer, bañador de rayas mujer


Chino Mujeres Cheongsam Qipao Señora Negro Estampado de Flores Vestido Largo Vestido de Novia Elegante Vestido (Color : Purple, Size : 3XL.)
- Material: poliéster, rayón
- Ropa tradicional china: Cheongsams
- Tipo de tejido: satén
- Duración: hasta el tobillo
- Decoración: Botón hecho a mano


TINGCHAO Brocado Jacquard Tela de satén de Seda Nupcial Tridimensional Noble Patrón de Flor de Textura de Lujo en Relieve Tela Delicada para Vestido de Novia 100X145cm,Rosado,A
- ☀ Exquisito patrón elegante: tejido de brocado avanzado de moda, refinado y hermoso. Briso y delicado, colorido, simple y elegante, muy cómodo. La tela es suave y transpirable, tiene una larga vida útil, muy distintiva, hermosa. Utilizado principalmente como ropa de mujer, como Custom Cheongsam, Vestidos. Saberable para todo tipo de ropa.
- ☀ Incorporando nuevos elementos de la nueva era, destacando el sentido de la calidad moderna. El patrón de tela jacquard es exquisito, con capas distintas y un fuerte sentido de tridimensionalidad, diseño novedoso, estilo único, sensación de mano suave, moda generosa y llena. de elegancia y nobleza ..
- ☀ Textura gruesa: la textura está bien, el brillo suave. El tejido de seda satinado se usa ampliamente en industrias textiles y prendas de vestir para diseñar vestidos, desgaste nocturno, bufandas y estolas .Firm y versátil, para vestidos de costura, camisas, medias faldas, cortotes, ropa de cama de cuatro piezas, cortina, etc., pero también se usa a menudo. Para hacer corbatas, colchas, mantas, cojines y otros artículos decorativos.
- ☀ Tela jacquard teñida de hilo: sensación y aspecto sedoso, material transpirable suave. Fácil de manejar, no arrugado. Muy adecuado para muchas artesanías y trabajos de costura, como hacer ropa. Puede cortar y coser fácilmente las telas con una máquina de coser y unas tijeras. La mano se siente bien y la drapea se siente bien.
- Regalo reflexivo: muy adecuado para muchas artesanías y trabajos de costura, puede cortar y coser fácilmente las telas con una máquina de coser y unas tijeras. El material es perfecto para la cubierta de almohada, la ropa, las bolsas, las chaquetas de telas nupciales. La tela es adecuada para disfraces, Diseño de interiores, vestidos de boda de brocado de seda exclusivos.


Clear Rhinestone Pearls Sash Boda Vestido De Novia Cinturón Accesorios para Fiestas - Blanco, 41 x 5 cm
- Magníficos accesorios para bodas, graduaciones, concursos y otras ocasiones formales
- Una pieza de fajín nupcial muy delicado
- Dimensión del aplique: 41 x 5 cm / 16.1 x 2 in
- Dimensión entera: 275 x 2 cm / 108.3 x 0.8 in
- Material: poliéster, aleación, diamantes de imitación


Vestido de Novia 1 Vestido de Novia Palabra Hombro Vestido de Novia Falda 2 Vestido de Novia Delgado Novia Posterior Grandes Yardas Formal/Blanco/m, L-F, Blanco, XXL
- Artesanía exquisita y única, destacando la alta calidad y el aseguramiento de la calidad.
- La selección de telas de malla de calidad crea un vestido de moda muy temperamental. El patrón elegante y de moda resalta su estilo dulce y elegante, tela de encaje cómoda, color brillante y hermoso romance.
- La cintura tiene un diseño de cintura único, simple y elegante, lleno de elegancia femenina, diseño de cintura alta, corte tridimensional, hermoso encaje, que muestra una figura elegante.
- Diseño de espalda abierta, brillante y sexy, hermosa espalda.
- El diseño romántico de los hombros resalta las fascinantes curvas de los hombros y el cuello, y las delicadas tallas de encaje muestran su elegancia.


Cosplay por MCCALL 's Cosplay m2028 AA, Vestidos de Novia con Mangas de cordón y Accesorios, tamaños 6 – 12
- La colección Vault
- Incluye las piezas del patrón e instrucciones para coserlo.
- Tejidos: arrugado gasa, seda, terciopelo, terciopelo, Jacquard, brocado
- Vestido con mangas de cordón y accesorios
- Impreso en los EE.


Patrón de Burda 6776 Vestido de Novia y Vestido de Fiesta
- 6776 Burda Wedding Dress Sewing Pattern Sizes 8-18
- 8-18


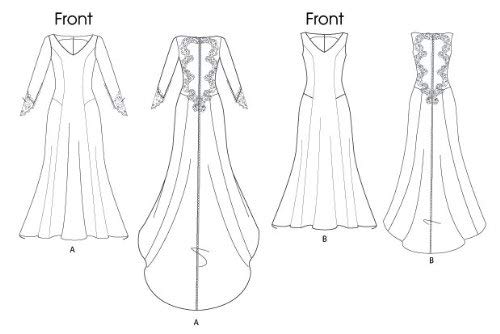
Butterick B5779 - Patrón de costura para confeccionar vestido de novia y de dama de honor
- El vestido alineado, subrayado tiene costuras de la princesa
- Corpiño ajustado, parte posterior del contraste, falda semi-cabida, dobladillo trasero formado y cierre/ajuste del lazo del botón trasero
- La espalda se extiende hacia la cola
- A: Manguitos largos y mangas inferiores de contraste con cierre de botones/bucle, B: sin mangas
- Nota: los motivos se cortan del tejido de encaje

Imágenes de Patron vestido novia
Si quieres elegir de forma visual los productos, aquí puedes ver una serie de fotografías de patron vestido novia. Pincha una de las fotos y accederás a la obtención online de colonia en concreto viendo sus peculiaridades y valor.