Tropical diseno grafico
Los mostradores de belleza y las tiendas on line de innumerables compañías de perfumes están llenos de lo último y lo mejor, así que ¿de qué manera sabes cuál será tu próximo destino? Pues te lo decimos nosotros: tropical diseno grafico, diseno de perfumes o perfumes y diseno. Así sea que se trate de olores florales, perfumes picantes, acordes de oud, o bien aromas dulces que le gusten, o bien que le guste la última y más grande fragancia en marcha o que sea un fanático de los viejos tradicionales, hemos reunido los mejores perfumes de todos y cada uno de los tiempos para inspirar su busca. No hay de qué. Así que para sostenerte en la nariz, hemos reunido las mejores olores nuevas de esta temporada, desde los lanzamientos de las grandes marcas que verdaderamente vale la pena probar, hasta las nuevas ofertas de nicho con un fuerte potencial de aroma de firma.
Listado top ventas para Tropical diseno grafico
Esperamos que con este grupo de productos puedas encontrar tropical diseno grafico al mejor precio y con la calidad óptima para el cuidado y bienestar de tu cuerpo. Nuestro objetivo es que podrás encontrar las mejores alternativas y precios de todo lo que necesitas para tu cuerpo, ofreciéndote la opción de descubrir varias marcas y modelos.

Maleta de Etiqueta de Equipaje de Cuero de PU, Correa de Cuero Ajustable Resistente a los arañazos, diseño Elegante Tropical Tress Gráficos
- Materiales de cuero de alta calidad PU con costuras mejoradas, sensaciones táctiles cómodas y durabilidad embellecer su itinerario.
- Una correa de extensión extraíble con hebilla de acero inoxidable, es fácil de adjuntar etiquetas a equipaje de diferentes tamaños.
- Las fundas de cuero PU aseguran la seguridad de su información personal, mientras que usted puede acceder fácilmente cuando usted lo necesita.
- Nuestras etiquetas de equipaje están disponibles para viajes, negocios, campamentos y caminatas. Distinguir su equipaje de los demás. Haga que sea más fácil encontrar su equipaje.
- Calidad garantizada, devolución libre defectuosa o cambio.


Havaianas Disney Stylish, Chanclas, para Unisex adulto, Verde Tropical, 39/40 EU
- Fabricado en Brasil
- Cómodo
- Resistente al agua
- Antideslizante
- Se adapta a la perfección


Tropical - Bolsa de la Compra, diseño de Taller gráfico


RXYY - Mochilas para niños con diseño de dinosaurios tropicales y letras del alfabeto, para viajes, mochila escolar, con correa para el pecho, para niñas y niños
- Dimensiones: 25,4 x 10,1 x 30,5 cm
- Material: hecho de tela de sarga, bolsa de red, ligero
- Diseño: cierre de cremallera, 1 compartimento principal con 1 compartimento interior, 1 bolsillo frontal con cremallera, 2 bolsillos laterales de malla; nuestro bapback tiene correa de hombro acolchada ajustable, fácil de ajustar la longitud adecuada; la correa de pecho con hebilla puede evitar que la correa de hombro de un niño se resbale, hay un silbato en la hebilla que un niño puede soplar en una emergencia para llamar la atención
- Aplicación: nuestra mochila es adecuada para 3 – 8 niños para viajar, ir al jardín de infancia preescolar o actividades diarias; el patrón personalizado puede ser un gran regalo
- Nota: no lavar a máquina, lavar a mano con delicadeza


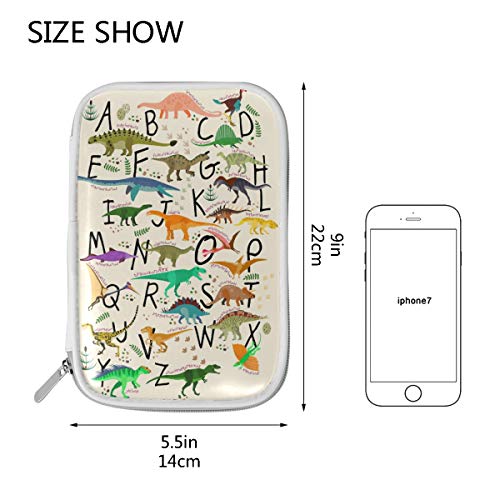
RXYY Estuche para lápices con diseño de dinosaurios tropicales, gráfico del alfabeto, soporte para lápices con cremallera, bolsa de viaje organizadora, cepillo cosmético, para niñas y niños
- Tamaño: 9 x 5,5 cm.
- Material: hecho de cuero de microfibra, durable
- Diseño: este estuche tiene 1 bolsillo de malla y 3 bolsillos con ranura. Podría ser mejor para guardar los artículos de papelería, como cepillos cosméticos. bolígrafos, lápices, clip, sacapuntas, borrador
- Multifuncional: el estuche es una bolsa con cremallera de gran capacidad, multifuncional, se puede utilizar como una bolsa grande para bolígrafos, bolsa de papelería, bolsa de cepillo cosmético, bolsa de pasaporte y bolsa para portátiles. ; Tacto suave, textura fina, forma encantadora
- Regalo perfecto: perfecto para amigos y padres como regalo de cumpleaños o Navidad.


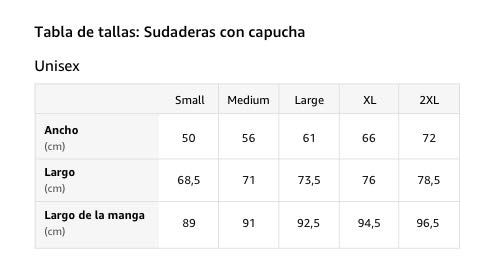
Diseño gráfico de una puesta de sol tropical y palmeras en Sudadera con Capucha
- Costa Rica Puesta de sol tropical y palmeras Diseño gráfico de la Costa Rica Mercantile Co - ¡Pura Vida!
- Para los amantes de Costa Rica, ya sea Nosara, Tamarindo, Puerto Viejo, Monteverde, Santa Teresa, o cualquier lugar de Costa Rica. Pura Vida, ¡disfruta!
- 241 gr, Encaje clasico, Cinta de sarga en el cuello


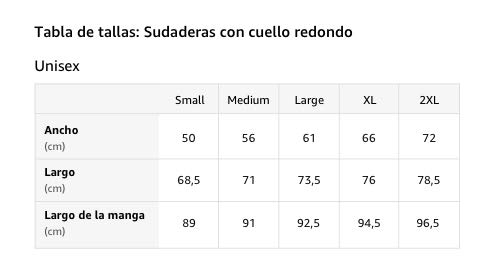
Diseño gráfico de una puesta de sol tropical y palmeras en Sudadera
- Costa Rica Puesta de sol tropical y palmeras Diseño gráfico de la Costa Rica Mercantile Co - ¡Pura Vida!
- Para los amantes de Costa Rica, ya sea Nosara, Tamarindo, Puerto Viejo, Monteverde, Santa Teresa, o cualquier lugar de Costa Rica. Pura Vida, ¡disfruta!
- 241 gr, Encaje clasico, Cinta de sarga en el cuello


Aloha Hibiscus Flowers Maui Sunset Hawaii Honolulu Hawaii PopSockets PopGrip Intercambiable
- Gran idea de diseño para cualquier persona que ama el verano, las fiestas de luau y la playa. A los surfistas les encantará este colorido diseño gráfico con flores tropicales de hibisco, palmeras, pájaros y patrón tribal tiki. Impresionante idea de diseño para familiares, amigos o para ti mismo.
- Este gráfico temático de Aloha incorpora la famosa cadena de isla hawaiana en un moderno logotipo elegante con Aloha en una fuente de escritura. Divertido recuerdo del estado de 50 para tus próximas vacaciones en Hawaii a Honolulu, Maui, Kauai, Oahu, Molokai o Lanai.
- PopGrip con top intercambiable; cambia tu PopTop por otro diseño o remuévelo completamente para las capacidades de carga inalámbrica. (No compatible con el cargador inalámbrico Apple MagSafe o la cartera MagSafe).
- Soporte expandible para ver videos, tomar fotos en grupo, FaceTime, Zoom y Skype manos libres.
- El adhesivo avanzado le permite quitar y reposicionar en la mayoría de los aparatos y estuches.
- Nota: no se adherirá a algunos estuches de silicona, impermeables o altamente texturizados.


Maui Sunset Hawaiian Hibiscus Flores Honolulu Love Hawaii PopSockets PopGrip Intercambiable
- Gran idea de diseño para cualquier persona que ama el verano, las fiestas de luau y la playa. A los surfistas les encantará este colorido diseño gráfico con flores tropicales de hibisco, palmeras, pájaros y patrón tribal tiki. Impresionante idea de diseño para familiares, amigos o para ti mismo.
- Este gráfico temático de Aloha incorpora la famosa cadena de isla hawaiana en un moderno logotipo elegante con Aloha en una fuente de escritura. Divertido recuerdo del estado de 50 para tus próximas vacaciones en Hawaii a Honolulu, Maui, Kauai, Oahu, Molokai o Lanai.
- PopGrip con top intercambiable; cambia tu PopTop por otro diseño o remuévelo completamente para las capacidades de carga inalámbrica. (No compatible con el cargador inalámbrico Apple MagSafe o la cartera MagSafe).
- Soporte expandible para ver videos, tomar fotos en grupo, FaceTime, Zoom y Skype manos libres.
- El adhesivo avanzado le permite quitar y reposicionar en la mayoría de los aparatos y estuches.
- Nota: no se adherirá a algunos estuches de silicona, impermeables o altamente texturizados.


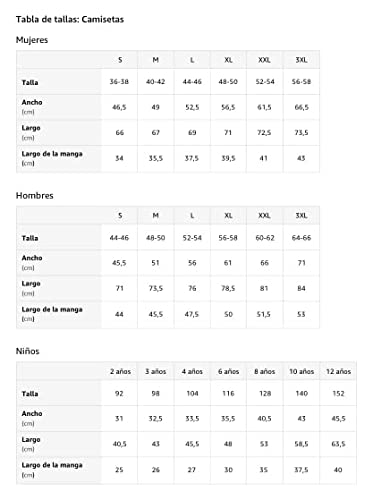
Señal de advertencia de ciclón tropical divertido diseño gráfico Camiseta
- Este es un diseño de advertencias de meteorología y ciencia meteorológica, perfecto para tormentas de huracanes y cazadores de tornados, úsalo y prepárate para interceptarlos, sentir la aventura y tocar el poder de la madre naturaleza y mostrar los efectos reales del cambio climático
- Cada año, varios países de todo el mundo se ven afectados por estos importantes fenómenos en el medio océano "Asia, África Europa y América", Atlantic Norte, Mar Caribe y Golfo de México, además del Pacífico Oriental, especialmente en Miami,
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Large Print Coloring Book Easy Flower Patterns: An Adult Coloring Book with Bouquets, Wreaths, Swirls, Patterns, Decorations, Inspirational Designs, and Much More!


3029 Sombreros de béisbol de Hip Hop de Color de Contraste Ajustable Hojas Tropicales diseño gráfico Palmas le Hojas Tropicales diseño gráfico Palmas Hipster Fitted Hat
- Material de la superficie: Cotton Denim (Single Layer).
- Detrás de un botón y se puede ajustar adecuadamente en tamaño.
- Sombrero para el sol, proteja su cabeza y rostro para el aire libre.
- Altura: Altura: 9 cm, Ala: 7 cm, Circunferencia del sombrero: 55-59cm (con botón ajustable en la parte posterior, Tamaño ajustable) Ajustable (55-60cm).
- Tiempo de entrega: 7-15 días laborables.


Diseño de gráfico de peces tropicales de arrecifes de coral Camiseta
- Diseño de gráfico de peces tropicales vintage retro de arrecifes de coral
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


Hig03j4 Gorra unisex para camionero, de algodón, ajustable, diseño gráfico de hojas tropicales, diseño gráfico, palmeras, diseño gráfico, palmeras, hipster, personalizada, de mezclilla
- Material de la superficie: algodón denim (una capa).
- Detrás de un botón y se puede ajustar correctamente en tamaño.
- Sombrero solar, protege tu cabeza y cara para exteriores.
- Altura: 9 cm, borde: 7 cm, circunferencia del sombrero: 55 – 59 cm (con botón ajustable en la parte posterior, tamaño ajustable) ajustable (55 – 60 cm).
- Tiempo de entrega: 7-15 días laborables.

Imágenes de Tropical diseno grafico
Si para ti es más cómodo elegir de forma visual los artículos, puedes observar aquí una agrupación de fotografías de tropical diseno grafico. Pincha en una de las imágenes y entrarás a la obtención online de colonia en concreto viendo sus funcionalidades y coste.