Rapado al 0 por los lados
Encontrar tu fragancia característica es como localizar la pareja perfecta: Raras veces sabrás lo que buscas hasta que lo halles. Todavía de esta manera, como en cualquier buena relación, tienes tus estándares, ¿cierto?? Tus rompecabezas, tu todo o bien nada. Mira si rapado al 0 por los lados, rapado al 1 con entradas o
Listado top ventas para Rapado al 0 por los lados
Te facilitamos nuestro listado de referencias gracias al cuál podrás encontrar rapado al 0 por los lados que se ajusten a los requisitos de tu cuerpo. Si quieres encontrar sinfín de opciones para comprar lo mejor para tu bienestar, te encuentras en uno de los mejores sitios web de la red.

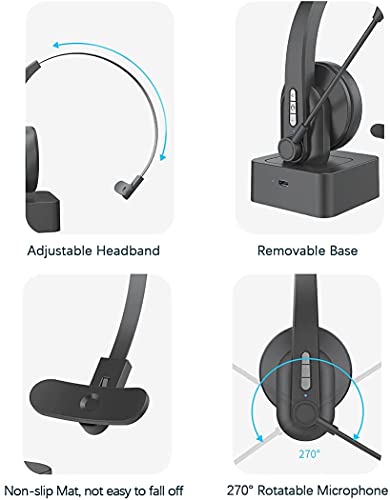
Bluetooth 5.0 Auriculares con Micrófonos, Auricular Bluetooth Cascos PC con Estación de Carga Cancelación de Ruido, Compatible con Servicio Telefónico,Manos Libres,Skype,Call Centers,Truck Driver
- 【Auriculares Bluetooth con Cancelación de Ruido】: Auriculares Bluetooth proporcionan un micrófono avanzado con supresión de ruido. La tecnología Bluetooth proporciona audio estéreo HD para llamadas y sonido multimedia.
- 【Tecnología Bluetooth 5.0】: Auriculares inalámbricos Bluetooth poseen el chip Bluetooth más avanzado, asegúrese de que la velocidad sea rápida y la conexión estable. Los auriculares bluetooth para teléfonos móviles pueden emparejarse con cualquier dispositivo habilitado para Bluetooth, incluidos los dispositivos Android e IOS.
- 【Base de Carga】: Base de carga a lo largo facilita la carga de los auriculares inalámbricos. Puede cargar los auriculares con un cable USB mediante powerbank.
- 【Tiempo de Espera de 100H】: Cargue 2 horas para recuperar 100 horas de tiempo de espera y 20 horas de tiempo de conversación. Este auricular bluetooth te permite hablar todo el día sin preocuparte por perder el contacto.
- 【Cómodo de Uso】: Almohadilla de espuma suave para los oídos y la diadema ajustable te ofrecen una sensación ultra cómoda incluso si trabajas duro todo el día. Puede hacer que se concentre en su conversación sin sentir ninguna carga en la cabeza y los oídos. Además, los micrófonos giratorios de 180 ° le permiten elegir usar el lado izquierdo o el derecho.


Logitech K120 Teclado con Cable Business para Windows, Tamaño Normal, Resistante a Líquido, Barra Espaciadora Curvada, PC/Portátil, Disposición QWERTY Español, color Negro
- Escritura Cómoda: Este teclado USB que permite escribir cómodamente durante mucho tiempo
- Encantador y Robusto: El teclado tiene diseño estándar con teclas F y teclado numérico de tamaño normal y es resistente, con un diseño resistente a salpicaduras y teclas duraderas
- Perfil Plano: El teclado tiene un perfil plano que añade elegancia al escritorio a la vez que permite mantener las manos en una posición más cómoda y natural
- Patas Ajustables y Robustas: Con las patas plegables desplegadas, la inclinación del teclado se incrementa en 8°
- Conexión Plug and Play: Se instala fácilmente, basta con conectarlo al puerto USB del ordenador de sobremesa, portátil o netbook, y ya se puede empezar a usar
- La Calidad Logitech: Descubre nuestros teclados para el español y ratones con cable, mini, inalámbricos o Bluetooth para el gaming o la oficina y accesorios para tablets, como Samsung Galaxy o iPad
- Prueba la Combinación Inalámbrica Logitech MK270: Para mayor libertad de movimiento con conexión inalámbrica fiable, botones de acceso rápido y directos a multimedia y duración de pilas prolongada
- Requisitos del sistema: PC con Windows (Windows XP, Windows Vista o Windows 7) o kernel Linux 2.6+; Puerto USB


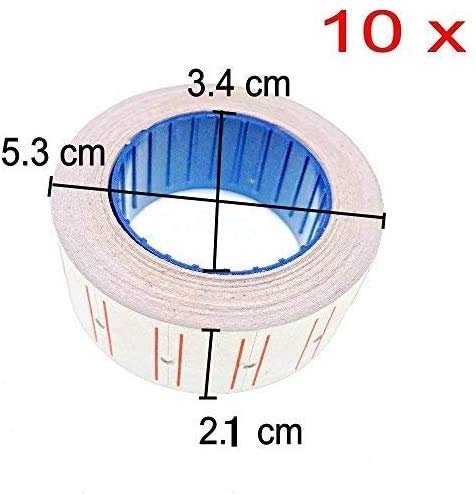
JZK® Etiquetadora pistola de precios 1 línea 8 caracteres precios al por menor kit de la pistola de etiquetas con 10 rollos de etiqueta y 2 cartuchos de tinta, rojo
- Los símbolos disponibles son: ¥, ฿, $, £, ₪, €, ₱, HK, R, RS, RP, RM, R$, ¢, +TX, BD, SR, EA,%, ., -, X, FOR, etc
- Los dígitos disponibles son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
- Esta etiqueta de precio de arma de etiqueta puede imprimir 7 dígitos y 1 unidad de dinero en una línea a lo sumo al mismo tiempo. Puede satisfacer sus diferentes necesidades para etiquetar diferentes precios
- Los dígitos y los símbolos se puede cambiar girando el mango negro en el lado. Fácil de usar
- Viene con 10 rollos de etiquetas (10 rollos x 500 etiquetas por rollo = 5000 etiquetas) y 2 cartuchos de tinta. Es suficiente para que lo uses por un tiempo.


Posca Coloring, PC-5M, paquete de 10 marcadores más vendidos
- Este juego de POSCA se compone de sus 10 marcadores de 5 M más vendidos.
- Escribe en metal, vidrio, plástico, piedra, tela, terracota, porcelana y muchos más, prácticamente cualquier superficie.
- La punta en forma de bala del 5M le da al usuario más control de línea, lo que le permite utilizar los aspectos más delgados y gruesos de su punta de 1,8 a 2,5 mm.
- El juego contiene 1 de cada uno de los siguientes bolígrafos: negro, blanco, rosa, rojo, amarillo, verde, azul claro, azul, dorado y plateado.

WOCCI 20mm Silicona Correa Reloj con Hebilla Plateada, Liberación Rápida para Hombre Mujer (Rosa Claro)
- Material de la Correa: Hecho de silicona ambiental de primera calidad con hebilla de acero inoxidable pulido. Las barras de resorte de liberación rápida le permiten cambiar las correas en unos segundos sin herramientas.
- Cómodo: Sin bordes afilados, suave al tacto, inodoro, ligero, flexible pero bastante resistente.
- Lavable e Impermeable: Perfecto para ejercicios al aire libre, deportes, cualquier tipo de entrenamiento o uso diario.
- Seleccionar Tamaño: Mide la distancia interior entre dos orejetas en la carcasa de tu reloj. La correa se ajustará a su reloj solo si el ancho de la orejeta del reloj es del mismo ancho que la correa.
- Compatible: Diseñado para adaptarse a la mayoría de los relojes tradicionales y relojes inteligentes con un ancho de orejeta estándar de 14 mm, 16 mm, 18 mm, 19 mm, 20 mm, 21 mm, 22 mm, 24 mm. No dude en contactarnos si tiene alguna pregunta o inquietud, nos comunicaremos con usted dentro de las 24 horas.

OliBoPo - Hebilla de acero inoxidable chapada en plata, resistente al agua, correa de reloj de goma de silicona
- - En varios colores. Puedes comprar colores diferentes y diseñar tu propio reloj.
- - Correa de goma de repuesto perfecta para reloj Swatch. Puedes confirmar el tamaño midiendo tu reloj como se muestra en el lado izquierdo de la imagen. No original, respuesto excelente. Deja que tu reloj tenga el mismo aspecto que el original.
- - Hecho de goma de silicona impermeable hipoalergénica con líneas antideslizantes en la parte posterior. Hace que se sienta ligero, resistente, suave y flexible durante el uso.
- - Con hebilla hipoalergénica de acero inoxidable chapada en plata, la correa es más duradera que otras hebillas de plástico.
- - Incluye juego de pasadores y una herramienta. Rápida y fácil de colocar y cambiar de correa en cuestión de segundos. Aunque la mayoría de las personas pueden hacerlo usando solamente los dedos, también incluimos una herramienta de ayuda por si te resultara necesario.


Mini Recambio espuma poro 0 de 11 cm. Pack de 10 uds.
- Recambio espuma moltopren poro cero Esponja en tamaño de 10 válido para varillas de Ø6 mm de 10 cm.
- Cono Ø 15 mm. Diámetro exterior 35 mm.
- Poliuretano base poliester. Extremo en corte recto Para acabados super finos con esmaltes, barnices y pinturas al agua (acrílicos al agua)
- Rodillos de espuma de alta calidad con dureza de compresión superfina con terminaciones rectas | en ambos lados Rodillos de espuma sin disolventes ni CFC para uso profesional
- Los rodillos de pintura de espuma son ideales para pinturas acuosas y de disolventes ligeros | El mejor acabado superficial gracias a los poros superfinos


LϟK 5 Pack Protector de Pantalla para Samsung Galaxy S21 Ultra 5G 6.8 Pulgada con 2 Pack HD Película de TPU y 3 Pack Protector de Lente de Cámara - Sin Burbujas Huella Digital Ultrasónica
- [Compatibilidad] - Incluye 2 unidades TPU Protector de Pantalla (No Cristal Templado) & 3 unidades Protector de Lente de Cámara (Cristal Templado) compatible con Samsung Galaxy S21 Ultra 5G 6.8 Pulgada.
- [Soporte Duradero para Mantener y Reemplazar] - Proporcionado por LϟK para garantizar la máxima protección durante la vida útil de su protector de pantalla.
- [Adhesivo único] - El TPU suave premium (película flexible) está diseñado exclusivamente para teléfonos de borde curvo para garantizar una protección de borde a borde. (Aplicación no mojada) (vidrio no templado), instalación sin burbujas y sin frustración que dejará la película perfectamente contorneada a cualquier dispositivo.
- [Ópticamente transparente] - Protector de pantalla 99% HD Clear con superficie lisa y sensación "Real Touch" y mantiene la calidad de imagen brillante y colorida.
- [Diseño específico] - Tecnología de corte láser precisa para ofrecer la máxima cobertura de pantalla. La flexibilidad del material permite la cobertura incluso en dispositivos curvos. Autocuración: uretano termoplástico flexible, resistente y de grado militar, diseñado para absorber el impacto. Touch-skin es resistente a arañazos, pinchazos, luz ultravioleta y no se amarilleará.

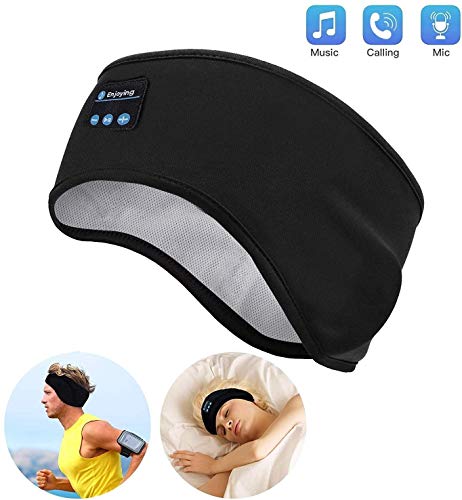
Auriculares para Dormir - Navly Bluetooth V5.0 Deportes Diadema | Deportiva Banda Auriculares con Ultrafinos HD Estéreo Altavoces,Perfectos para Deportes, Dormir de Lado, Viajes Aéreos y Relajación
- 【Auriculares de Sueño y Diadema Deportiva 2 en 1】La diadema deportiva Bluetooth puede escuchar música maravillosa, también le da un ambiente tranquilo o encantador de sueño profundo. Sin tener que llevar auriculares adicionales, protege de que te moleste el cabello y el sudor.Como auriculares para dormir, le permite dormir profundamente en cualquier lugar y no dañará sus oídos.
- 【Avanzada Bluetooth 5.0 Tecnología】La tecnología Bluetooth ha hecho un avance importante en esta generación de auriculares de sueño.Sports Headband se empareja con cualquier teléfono inteligente o tableta con Bluetooth habilitado más rápido y fácil.Alcance inalámbrico de 45 pies, potencia ultrabaja, batería recargable de alta capacidad de 240 mAh incorporada.
- 【Cómoda Diadema Elástica Suave】Construido con imanes de altavoz estéreo de 12.5 mm y micrófono que ofrecen un sonido digital claro y de alta calidad.Diadema de música elástica, adecuada para cualquier tipo de cabeza.Diadema que no se mueve ni se cae mientras duerme o corre.
- 【Ajuste Perfecto para Deportes o Sueño】Estos auriculares para dormir son la ayuda perfecta para dormir y combatir el insomnio.Bloquean el ruido ambiental sin usar tapones para los oídos que son dolorosos y se caen.Un regalo único y divertido para amigos y familiares. Sorpréndelos con estas diademas súper cómodas, transpirables y livianas.
- 【Nota】El forro de tela separado de las costuras no es defectuoso, es el lugar para sacar el módulo Bluetooth, por lo que puedes lavar completamente la diadema.El voltaje de salida recomendado del cargador es DC5V, y la corriente de salida recomendada es de 100 mA a 500 mA.Si tiene algún problema o pregunta, contáctenos aquí, seguramente haremos nuestro mejor esfuerzo para ayudarte.


SteelSeries QcK Mini, Alfombrilla de Ratón de Juego, 250 mm x 210 mm (Tela, Base de Caucho, Compatible con Ratón Láser y óptico), Negro
- Tela exclusiva de microtejido QcK para un control máximo
- Optimizada para movimientos de seguimiento de DPI bajos y altos
- Duradera y lavable para una fácil limpieza
- La base de goma antideslizante elimina los movimientos no deseados
- QcK es la mejor opción para los profesionales de esports durante más de 15 años


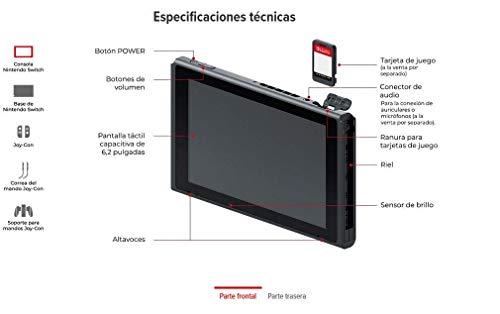
Nintendo Switch - Consola Estándar - Gris
- La nueva Switch añade dos horas más de batería en comparación al modelo antiguo, para pasar de entre 3 y 6 horas de duración, a entre 4 y 9 horas
- Nintendo Switch se transforma para adaptarse a tu situación y te permite jugar a los títulos que quieras aunque no tengas mucho tiempo.Es una nueva era en la que no tienes que adaptar tu vida a los videojuegos: ahora es la consola la que se adapta a tu vida.
- Tres modos de juego: 1- Modo televisor (Reune a todos ante una pantalla y disfruta del juego en compañía. Coloca la consola en la base de la Nintendo Swith para jugar en alta definición en el televisor) 2- Modo sobremesa (Comparte la pantalla, comparte la diversión. Abre el soporte de la consola para compartir la pantalla y pasarlo en grande con juegos multijugador) 3 - Modo portatil (Lleva contigo una espléndida pantalla allá donde vayas. Juega con los mandos Joy-Con encajados en la consola y llévatela donde quieras)
- Nintendo Switch tiene dos mandos, uno a cada lado de la consola, que funcionan juntos: los Joy-Con. Si acoplas los dos Joy-Con al soporte para mandos Joy-Con, funcionarán como un mando convencional, mientras que por separado funcionarán como dos mandos individuales plenamente funcionales.
- Conecta hasta ocho consolas para partidas multijugador
- Compatible con tarjetas de memoria microSD, microSDHC y microSDXC. Los datos de juego que no quepan en la memoria de la consola podrán almacenarse en estas tarjetas. Nota: se requiere una actualización a través de internet para usar tarjetas de memoria microSDXC


Logitech G403 Lightspeed Ratón Gaming, Captor HERO 16.000 DPI, Pesos Ajustables, 6 Botones Programables, Memoría Integrada, Compatible con PC/Mac, Negro
- Captor HERO 16K: Nuestro sensor más sofisticado, con seguimiento 1:1, 400+ IPS y una sensibilidad máxima de 100-16.000 dpii
- RGB LIGHTSYNC: La iluminación RGB de espectro completo determinada por el juego responde a la acción de juego, al audio y al color de la pantalla y se sincroniza con los dispositivos y accesorios G
- Comodidad Y Calidad Supremas: G403 es ligero, con un diseño cómodo, para amoldarse a tu mano y con recubrimiento de goma para mayor control
- G Hub: Configura seis botones programables mediante Logitech G HUB para simplificar tus acciones de juego; personaliza tu configuración de sensibilidad de dpi de 100 a 16.000 dpi
- Rendimiento de Gaming óptimo: Con un tiempo de respuesta de 1 ms, G403 es hasta 8 veces más rápido que los ratones estándar no diseñados específicamente para gaming
- Actualice a 25K DPI: aumente el DPI máximo a 25,600 para desbloquear el primer nivel de rendimiento submicrónico del mundo (disponible para todos los ratones con el sensor HERO 16K a través de una actualización de software de G HUB)


Auriculares para Dormir - Navly Bluetooth V5.0 Deportes Diadema | Deportiva Banda Auriculares con Ultrafinos HD Estéreo Altavoces, Deportes, Dormir de Lado, Viajes Aéreos y Relajación
- 【Auriculares de Sueño y Diadema Deportiva 2 en 1】La diadema deportiva Bluetooth puede escuchar música maravillosa, también le da un ambiente tranquilo o encantador de sueño profundo. Sin tener que llevar auriculares adicionales, protege de que te moleste el cabello y el sudor.Como auriculares para dormir, le permite dormir profundamente en cualquier lugar y no dañará sus oídos.
- 【Avanzada Bluetooth 5.0 Tecnología】La tecnología Bluetooth ha hecho un avance importante en esta generación de auriculares de sueño.Sports Headband se empareja con cualquier teléfono inteligente o tableta con Bluetooth habilitado más rápido y fácil.Alcance inalámbrico de 45 pies, potencia ultrabaja, batería recargable de alta capacidad de 240 mAh incorporada.
- 【Cómoda Diadema Elástica Suave】Construido con imanes de altavoz estéreo de 12.5 mm y micrófono que ofrecen un sonido digital claro y de alta calidad.Diadema de música elástica, adecuada para cualquier tipo de cabeza.Diadema que no se mueve ni se cae mientras duerme o corre.
- 【Ajuste Perfecto para Deportes o Sueño】Estos auriculares para dormir son la ayuda perfecta para dormir y combatir el insomnio.Bloquean el ruido ambiental sin usar tapones para los oídos que son dolorosos y se caen.Un regalo único y divertido para amigos y familiares. Sorpréndelos con estas diademas súper cómodas, transpirables y livianas.
- 【Nota】El forro de tela separado de las costuras no es defectuoso, es el lugar para sacar el módulo Bluetooth, por lo que puedes lavar completamente la diadema.El voltaje de salida recomendado del cargador es DC5V, y la corriente de salida recomendada es de 100 mA a 500 mA.Si tiene algún problema o pregunta, contáctenos aquí, seguramente haremos nuestro mejor esfuerzo para ayudarte.


6 Pares de Acero Inoxidable Hombres espárragos Pendientes para Hombres Damas Pendientes de aro Negro Huggie Piercing Pendientes Pendientes Clip Pendientes
- MATERIAL: acero inoxidable; Está hecho de acero inoxidable libre de alergias, ¡por lo que el color nunca se desprende! Él también tiene una vida larga, lo que sin duda determina la calidad a un buen precio. El acero inoxidable no contiene níquel, no contiene plomo, no contiene cromo y es ecológico.
- BENEFICIOS: Hacemos 6 pares como una configuración: 6 estilos diferentes, permitiéndole usar los diferentes tapones para las orejas.
- REGALO: un accesorio único para hombres y mujeres. Un regalo ideal para regalar o para ti. Se adapta a la mayoría de los Klied, ¡muy ajustados al vestido de noche!
- EMBALAJE: Con una envoltura de regalo hermosa y lujosa, los productos pueden obtener una mejor protección.
- Tamaño como se muestra en la imagen


Kono Maleta de Cabina de ABS de 20 Pulgadas con Diseño Esculpido en Horizontal,4 Ruedas,55x40x22cm
- ✅✈Maleta de Cabina - 55x40x22 cm (Todas las partes), 2,5 kg;Carcasa resistente de ABS para asegurar la protección contra los golpes.
- ✅✈Equipaje de Mano Cabina-Los cuatro pares de ruedas giratorias distribuyen equitativamente el peso de tu maleta y permiten deslizarla fácilmente en aeropuertos o estaciones de tren concurridos.
- ✅✈Manija retráctil y cómoda con tres niveles de altura.Tiene dos asas normales, una en la parte superior y otra en el lateral.
- ✅✈Un candado incorporado con clave de 3 dígitos para una máxima seguridad.Cuatro pies de plástico en el lateral para mantener la maleta estable al dejarla en el suelo.
- ✅✈Apertura central para hacer la maleta de manera organizada - Cintas de nailon cruzadas con hebilla para ajustarlas y así proteger el contenido en un lado. El otro lado tiene un separador con cremallera para proteger el contenido del otro lado.

Imágenes de Rapado al 0 por los lados
Si a ti te es más cómodo elegir de forma visual los productos, mira aquí una agrupación de fotografías de rapado al 0 por los lados. Pincha con el ratón en una de las fotos y accederás a la compra online de colonia en concreto viendo sus funcionalidades y costo.