Formula para hacer colonia
Existen muchos perfumes en el mercado y en cualquier tienda de venta al público online. No obstante, no se puede estar seguro de su longevidad y calidad. Dale una oportunidad a referencias como formula para hacer colonia, hacer colonia para bebes o hacer ambientador con colonia y ya verás como vas a oler mucho mejor!. Cómo se huele afirma mucho sobre quién es uno, en especial en un mundo donde las primeras impresiones ahora significan todo. Ciertas personas elegirán un olor diferente toda vez que compren un nuevo frasco, a algunos les puede gustar adherirse a una etiqueta en particular, e inclusive hay quienes escogen una olor por siempre - un fragancia que sienten que los define como persona. A continuación se presentan algunas de las mejores opciones de colonia para hombres y mujeres, escogidas por los especialistas en estilo y aseo de nuestra tienda online. Todos estos productos vienen de diseñadores que saben todo acerca de la elaboración de un perfil de fragancia atrayente.
Listado top ventas para Formula para hacer colonia
Descubre nuestro listado de referencias gracias al cuál podrás encontrar formula para hacer colonia que tengan las necesidades de tu salud. Te aseguramos que llegarás a encontrar las mejores opciones y precios de todo lo que estés buscado para tu bienestar, dándote la oportunidad de descubrir numerosas referencias y marcas.

Adiós ESTREÑIMIENTO. Remedios Naturales, Terapias Alternativas y Complementarias.


Probióticos y Prebióticos Intestinales | Con Inulina y Glutamina | Sistema Inmunológico, Colon Irritable y Más | 90 Cápsulas | Repara Flora Intestinal y Vaginal | Amplio Espectro | 60 Mil Millones UFC
- POR QUÉ ESTE PROBIÓTICO Y NO OTRO: En Magister Fórmula desarrollamos este producto en base a lo que nos pedían nuestros clientes, un probiótico y prebiótico de calidad y liberación prolongada con la tecnología patentada de Megaflora9 EVO (ProbioAct ) y la Glutamina, los cuales forman una combinación perfecta para potenciar la salud intestinal y digestiva natural de las bacterias buenas en el organismo.
- MÚLTIPLES BENEFICIOS: Con 2 cápsulas al día, 1 antes del desayuno y 1 antes de la cena obtendrás una dosis garantizada de 60 Mil Millones de UFC (Unidades Formadoras de Colonias) con los siguientes beneficios: aumento del sistema inmune, mejora las defensas, alivio de trastornos gastrointestinales (Colon Irritable, Diarreas, Aerofagias, Estreñimiento, Intolerancias Alimentarias). Mejora de neurotransmisores (Eje Intestino-Cerebro), trastornos cutáneos y reparación de flora intestinal y vaginal.
- PROTEGE Y REPARA LA MUCOSA INTESTINAL: Además, hacemos uso de la GLUTAMINA, un potente reparador de la mucosa que recubre nuestro intestino. Así, se mejora la función barrera y la permeabilidad de la mucosa, lo que impide que penetren toxinas y permita una correcta absorción de los nutrientes. De igual manera, este aminoácido crea un entorno muy favorable para que se reproduzcan las bifidobacterias y lactobacillus presentes en Megaflora9 (los probióticos).
- TECNOLOGÍA PATENTADA (COMPARATIVA): usamos la tecnología ProbioAct bajo patente, que protege las bacterias contra las condiciones ácidas del estómago y las mantiene vivas, asegurando una supervivencia superior al 90% (frente a un 1% de otras marcas). Gracias a ello, combinamos 9 cepas de bacterias de tipo Lactobacillus, Bifidobacterias y Enterococcus, que juntas repoblan la microbiota dañada del intestino de forma eficaz. Además es apto para veganos, hombre, mujer y niños.
- CALIDAD FARMACÉUTICA PROFESIONAL: En Magister Fórmula llevamos más de 130 años de experiencia ayudando a farmacias de toda España, por lo que puedes estar seguro de que nuestros productos son eficaces y elaborados bajo los más altos estándares de calidad europea, sin usar aditivos artificiales, saborizantes, conservantes, colorantes, sin lactosa, gluten ni componentes animales. Y cuenta con la calificación de QPS (Quality Presumption of Safety).


Bestme Baco Fórmula Antioxidante para la limpieza del higado. I Efectos Anti Resaca I Para Digestiones Pesadas. I Detox Hígado I Cardo Mariano I Alcachofa I Cisteina y mucho más I 60 Cápsulas
- ✅Alivio del dolor y la inflamación cerebral (por la acción del Acido Alfa Lipoico y el aporte completo de Vitaminas y Minerales). N europrotector cerebral. 🧠. Analgésico y calmante estomacal.
- ✅Recuperación electrolítica de Sales Minerales con alto aporte de Vitaminas del grupo B (B complex) . ASimismo la fórmula incluye antioxidantes que desintoxican con efectos drenantes haciendo una profunda limpieza del Higado tras la ingesta de Alcohol (Anti Resaca) , comidas grasas, exceso de azúcar, gracias al aporte del Aminoácido NAC, Cardo Mariano, ( milk thistle ) Extracto de Alcachofa
- ✅Restablece y regula el sistema metabólico (efectos depurativos). Eliminador de nauseas y malestar global. Incluye Extracto de Jengibre (Ginger) , Manzanilla y Uva ✔
- ✅ Sabemos que la combinación correcta de nutrientes puede hacernos más fuertes, más rápidos, más equilibrados y más energéticos. Con años de ciencia detrás y una investigación avanzada a nuestro alcance, creamos combinaciones poderosas de vitaminas, minerales, fitonutrientes y aminoácidos para que tu cuerpo y mente puedan sentir y rendir al 100%:
- ✅Producto 100% natural que goza del pertinente Código Farmacéutico Nacional y esta producido bajo Certificación ISO 9001.

Kijimea Colon Irritable Pro, Una Terapia Contra El Síndrome del Colon Irritable (Diarrea, Dolor Abdominal, Flatulencia, Estreñimiento), Producto Vegano, Sin Gluten ni Lactosa, Verde, 84 cápsulas
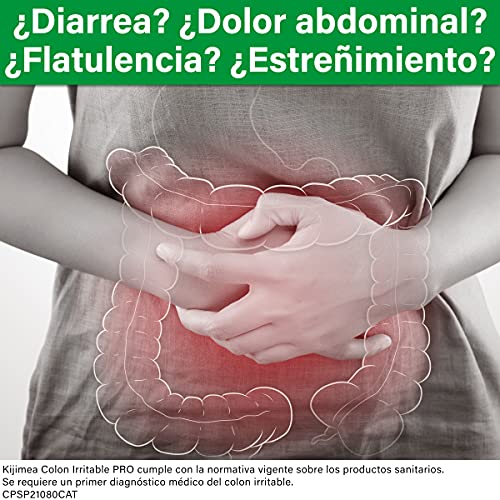
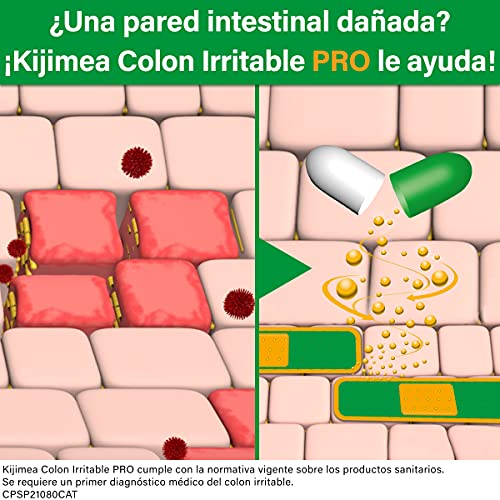
- 🩹Como un parche para el intestino. Las bifidobacterias B. bifidum HI-MIMBbb75 se adhieren a las zonas dañadas de la pared intestinal, como un parche. Bajo este parche puede regenerarse la pared intestinal. Las típicas molestias intestinales disminuyen.
- ✅ Ayuda eficaz. La eficacia de Kijimea Colon Irritable PRO para la diarrea recurrente, el dolor abdominal, la flatulencia y el estreñimiento fue demostrada por científicos alemanes en estudio de productos de venta libre del mundo sobre el síndrome del intestino irritable.
- 🏅 Mayor calidad de vida. La diarrea recurrente, el dolor abdominal, la flatulencia o el estreñimiento pueden hacer que disminuya mucho la calidad de vida. Un reciente estudio clínico demuestra que Kijimea Colon Irritable PRO es capaz de mejorar significativamente la calidad de vida de los afectados.
- 🔬 Sin efectos adversos conocidos. Kijimea Colon Irritable PRO tiene buena tolerabilidad y se desconocen efectos adversos o interacciones con otros medicamentos.
- 🌱 Vegano, sin gluten ni lactosa. Apto para pacientes con diabetes.
- ☑ Kijimea Colon Irritable cumple con la normativa vigente sobre los productos sanitarios. Se requiere un primer diagnóstico médico del colon irritable; CPSP21080CAT


Domina Tus Emociones: Una guía práctica para superar la negatividad y controlar mejor tus emociones: 1 (Colección Domina Tu(s)...)


BELLY Colonia para Perros, Esencia Lavanda y Pomelo - Colonia Perros Cachorros y Adultos - Perfume Perro, Refrescante e Hidratante - Desodorante Perro, Aroma Duradero - Colonia Mascotas Vegana, 250ml
- 🐶 PERFUME PARA PERROS CON AROMA DURADERO: Nuestra colonia para perros BELLY Neat Dog, con esencia de lavanda y pomelo, es la solución natural perfecta para proporcionar a tu perro el mayor cuidado posible, dejándole un aroma agradable, refrescante y duradero
- 🐶 DEJA EL PELO SUAVE E HIDRATADO: El innovador perfume para perros BELLY Neat Dog con fragancia de lavanda y pomelo contiene extracto de aloe vera, que hidrata profundamente y suaviza el pelaje de tu amigo de cuatro patas, dándole una sensación duradera de frescura
- 🐶 FÓRMULA NATURAL: A diferencia de otras colonias para perros, este spray está formulado con aceites esenciales naturales que neutralizan eficazmente los malos olores y son respetuosos con el pelaje de tu mascota. Es seguro de usar alrededor de niños, gracias a su fórmula libre de tóxicos
- 🐶 PRÁCTICO Y FÁCIL DE USAR: BELLY Neat Dog es práctico y fácil de usar gracias a su spray con nebulizador. Simplemente debes rociar el spray sobre el pelaje seco o mojado de tu perro y esperar a que se seque antes de cepillar. Es ideal para viajes, después de un paseo o incluso luego de un baño
- 🐶 FABRICADO EN ALEMANIA: Todos nuestros productos han sido creados y testados en Alemania. Utilizamos solo ingredientes de la más alta calidad, libres de crueldad animal, y mejoramos constantemente las fórmulas utilizadas para crear los mejores productos posibles


Digestic – Laxante para Aliviar el Estreñimiento – Ablanda las Heces – Ingredientes 100% Naturales – 60 Cápsulas – Nueva Fórmula Innovadora Limpieza Detox del Colon
- 🔬 EL FRUTO TRAS 18 AÑOS DE INVESTIGACIÓN CIENTIFÍCA: ¿Estás cansado de productos para el estreñimiento que no funcionan? ¿Cansado de pastillas laxantes, jugo de ciruelas pasas, tés, probióticos, enzimas digestivas y enemas que no brindan alivio?Descubre la innovadora solución científicamente probada para aliviar eficazmente los síntomas de estreñimiento. Usa Digestic, un suplemento 100% vegetal y natural para aliviar el estreñimiento crónico.
- ✔ ALIVIO PURO: Alivia rápidamente y promueve la salud óptima del colon regulando la función intestinal y el sistema digestivo. Fortalece y favorece la contracción de los músculos estomacales para la evacuación diaria. Digestic actúa como un eficaz laxante natural para aliviar el estreñimiento.
- 💪 FÓRMULA REVOLUCIONARIA: Revolucionario laxante vegetal natural, formulado con ayudas digestivas así como estimulantes para la digestión. Limpieza natural Detox. Una mezcla única de hierbas y productos botánicos que alivian el estreñimiento, la hinchazón y los gases. Ablanda naturalmente las heces, que favorecen la salud intestinal y sus movimientos.
- 🌱 INGREDIENTES NATURALES: Carica Papaya, Aloe Ferox, Cassia Angustifolia, Rhamnus Frangula, Rhamnus Purshiana, Elettaria Cardamome, Foeniculum Vulgare.
- ✔ SEGURO Y EFICAZ: Clínicamente probado, sin efectos secundarios, no adictivo. No forma hábito. Seguro para el uso diario y a largo plazo. Fabricado cumpliendo las normas GMP, En una instalación registrada en la FDA.
- ★Satisfacción 100% garantizada★: Respaldamos nuestro producto con confianza. Si de alguna manera no estás completamente satisfecho con nuestro producto, por favor, háznoslo saber antes de 30 días, te devolveremos el dinero.


Detox Depurativo Higado y Colon Diurético Natural | Complejo Bio Alcachofa Rábano Negro Cúrcuma Orgánica | Drenante Desintoxicante Digestión Limpieza Intestinal | Vegano 90 Cápsulas Hecho en Francia
- DIURETICO NATURAL : Suplemento Natural Para El Hígado, Potente Detox Cleanser combinación de cuatro Hierbas Naturales, Alcachofa Rábano Negro y Cúrcuma. Suplementos Naturales desintoxica tu organismo y mejora tu digestión. Perder el exceso de líquido y las retenciones de agua son uno de los grandes pasos hacia el adelgazamiento. Favorece una buena digestión, mejora el tránsito intestinal y de colon.
- DESINTOXICAR CUERPO : Ayuda a tu dieta quemar grasa para eliminar, depurar y drenar el organismo. Ayuda a reducir las calorías ingeridas de carbohidratos, azucares y grasas. Combate la acumulación de liquidos. Ayuda a disminuir el almacenamiento de la grasa acumulada en el cuerpo. Es un complemento alimenticio, que mediante su uso eliminaremos líquidos, mejoraremos nuestra piel y nuestro metabolismo. Contribuye a la pérdida de peso y elimina las toxinas y los desechos del cuerpo
- DEPURATIVO HIGADO : Este complemento alimenticio Detox Natural con hierbas naturales ayuda al control del colesterol en el hígado, ayuda a bajar de peso y también facilita el adecuado metabolismo de las grasas. Activa el drenaje hepático y alivia los trastornos digestivos. Contribuye a la buena digestión favoreciendo la eliminación de los gases evitando así que causen molestias e hinchazón abdominal. Actua a nivel intestinal facilitando la emulsión de las grasas y regulando su absorción.
- ELIMINA TOXINAS : La Alcachofa mejora el funcionamiento de los riñones, haciendo que todo el proceso de orinar sea mucho más rápido y fluido, evitando la retención de líquidos. El Rábano Negro favorece al drenaje tanto del hígado como de la vesícula biliar, por lo que ayuda a la eliminación de toxinas y residuos. Ayuda a mejorar la digestión y la desintoxicación del cuerpo. La Curcuma tiene propiedades antioxidantes, antiinflamatorias y depurativas. Prode origen vegetal
- PRODUCTO NATURAL : Cápsulas de origen vegetal. Todos los ingredientes provienen de la agricultura biologica. Podrucido y Fabricado en Francia. Programa completo para un mes. Una fórmula específica para reducir la grasa de las piernas, drena el exceso de liquidos. - **ATENCIÓN : No se deje engañar con productos similares de bajo precio, que pueden causarle daños irreparables al organismo por ser de dudosa procedencia.**


Colon Gel Activo - Detergente para lavadora, adecuado para ropa blanca y de color, formato gel - pack de 5, hasta 170 dosis
- Detergente para la lavadora formato gel
- Profundo poder quitamanchas, eliminando las manchas de tu ropa incluso en agua fría
- Extra luminosidad en tus prendas blancas y de color
- Ropa sin manchas, limpia y con un plus de luminosidad
- Descubre el resto de detergentes y limpialavadoras de Colon


4711 Agua de Colonia - 150 ml
- Tipo de producto: agua de colonia
- Género : unisex adultos
- Marca : 4711


Relec Extra Fuerte Spray Antimosquitos | Repelente de Mosquitos Eficaz contra el mosquito tigre | Desarrollado para evitar las picaduras de mosquitos en severas condiciones climáticas | 75ml
- El spray antimosquitos te protege eficiente de las picaduras de insectos en severas condiciones clímaticas y ambientales; óptimo para usar lo en países tropicales
- Formulado con deet 50%, aceite de lavanda y geraniol, eficiencia óptima y larga duración, deja un agradable aroma sobre la piel; protege contra malaria, zika, fiebre amarilla, dengue o chikungunya
- La presentación en spray es fácil de aplicar, protector en zonas con alto riesgo de transmisión de enfermedades tropicales; alta protección y eficaz contra la familia del mosquito tigre
- Repelente para mosquitos de viaje especialmente indicado para viajeros a países tropicales; adecuado para lugares con un clima tropical, hasta 9 horas de protección, spray de 75 ml
- Relec es una gama de productos de eficacia óptima y seguridad que protege a tu familia de las picaduras de insectos en cualquier situación


Elena - Formula Gel Profesional para limpiar, pack de 2x4.9 kg
- Detergente liquido
- Formato Profesional
- Fragancia fescor colonia
- Formato ahorro
- Pack de 146 lavados

![Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses) Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses)](https://www.iesribera.es/pics/2020/09/16/probiotico-60-mil-millones-de-cfu-de-aavalabs-15-cepas-bacterianas-por-porcion-formula-de-amplio-espectro-de-alta-potencia-60-capsulas-sumini-6712.jpg)
Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses)
- ➤ 15 CEPAS PROBIÓTICAS DE LIBERACIÓN PROLONGADA: Nuestro complejo de cultivos único de cepas probióticas contiene una variedad de cepas bacterianas patentadas, cuya eficacia para actuar directamente en numerosas partes del tracto digestivo humano ha sido demostrada científicamente. Seguros frente a los ácidos del estómago, nuestros probióticos viajan a través de tu sistema digestivo con DRCaps, llegando incluso al intestino delgado, en donde se encuentra la mayor parte de la flora intestinal.
- ➤ MEJORA DE LA FLORA DIGESTIVA Y DEL SISTEMA INMUNE: Tu tracto digestivo es responsable de mucho más que simplemente proporcionar a tu cuerpo todas las vitaminas, nutrientes y minerales esenciales. Más de 2/3 de tu inmunidad depende de tu flora intestinal. Nuestro probiótico de amplio espectro es una elección totalmente natural para conseguir un intestino sano y reforzar las defensas. También está diseñado para ayudar a tu sistema inmunológico gracias al zinc añadido de forma natural.
- ➤ 30 MIL MILLONES DE UFC GARANTIZADAS: Te garantizamos que todas y cada una de las cápsulas retendrán 30 mil millones de UFC hasta el final de la vida útil indicada del producto. Esto es debido a su tecnología de microencapsulación patentada, que garantiza además la efectividad del producto.
- ➤ LIMPIO, FORMULADO CIENTÍFICAMENTE Y PROBADO EN LABORATORIOS: La trifecta de oro. Nuestro probiótico no contiene gluten, lactosa ni productos modificados genéticamente, y además es 100% vegano. Ha sido elaborado en Europa, bajo estrictos estándares, para que puedas tener la tranquilidad de que estás tomando un producto seguro y limpio, fabricado por una marca nórdica.
- ➤ GARANTÍA DE SATISFACCIÓN DE 365 DÍAS: Te ofrecemos una increíble oferta de 60 cápsulas, con un suministro para 2 meses, para que puedas probar nuestro probiótico y experimentar rápidamente sus increíbles beneficios. En caso de que sientas que nuestro probiótico no ha cumplido tus expectativas, puedes conseguir el reembolso del 100%. Es así, ¡te devolveremos el dinero aunque devuelvas el frasco vacío!


Jennifer Lopez Glow - Eau de toilette, 100 ml
- Corazón: rosa, ámbar, madera de sándalo
- Notas altas: pomelo y flor de azahar
- Notas de fondo: jazmín y vainilla
- Fragancia de la casa de diseño de Jennifer Lopez
- El halcón, con suaves líneas curvas, recuerda al cuerpo de una mujer
- La joyería de la botella está inspirada en el estilo personal de J.Lo

Imágenes de Formula para hacer colonia
Si quieres elegir de forma visual los productos, puedes observar aquí una serie de fotos de formula para hacer colonia. Haz click con el ratón en una de las imágenes y accederás a la obtención online de perfume en concreto viendo sus atributos y coste.














































![Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses) Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses)](https://www.iesribera.es/pics/2020/09/16/probiotico-60-mil-millones-de-cfu-de-aavalabs-15-cepas-bacterianas-por-porcion-formula-de-amplio-espectro-de-alta-potencia-60-capsulas-sumini-6712-2.jpg)
![Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses) Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses)](https://www.iesribera.es/pics/2020/09/16/probiotico-60-mil-millones-de-cfu-de-aavalabs-15-cepas-bacterianas-por-porcion-formula-de-amplio-espectro-de-alta-potencia-60-capsulas-sumini-6712-3.jpg)
![Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses) Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses)](https://www.iesribera.es/pics/2020/09/16/probiotico-60-mil-millones-de-cfu-de-aavalabs-15-cepas-bacterianas-por-porcion-formula-de-amplio-espectro-de-alta-potencia-60-capsulas-sumini-6712-4.jpg)
![Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses) Probiótico [60 mil millones de CFU] de AAVALABS - 15 Cepas Bacterianas por Porción - Fórmula de Amplio Espectro de Alta Potencia - 60 Cápsulas (Suministro de 2 Meses)](https://www.iesribera.es/pics/2020/09/16/probiotico-60-mil-millones-de-cfu-de-aavalabs-15-cepas-bacterianas-por-porcion-formula-de-amplio-espectro-de-alta-potencia-60-capsulas-sumini-5.jpg)





