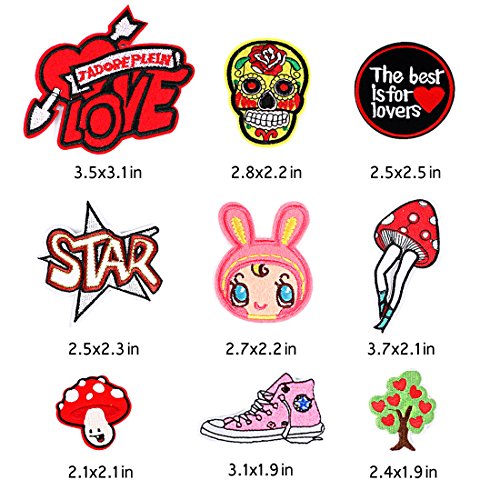
Aplicaciones para camisetas infantiles
A todos nos gusta olfatear bien. Puede hacer que tu día sea perfecto. En la actualidad las fragancias son fundamentales en tanto que no solo combaten el olor corporal, sino también ayudan a aumentar la confianza. Olisquear el placer tiene otros beneficios también, como la reducción del agobio y los efectos del insomnio. Prueba con aplicaciones para camisetas infantiles, apliques para camisetas o camisetas ed hardy para mujer y mejora tus experiencias. Una gran fragancia es algo poderoso. Puede hacer que te sientas unido en un enorme día, ponerte de buen humor, e incluso hacer que la gente te recuerde, conque hallar la correcta es extremadamente esencial. La parte más esencial de toda esta ecuación: tu propia nariz. Deseas localizar una colonia que te huela bien inmediatamente. Apégate a una fragancia que no choque con otros olores fuertes y que no sea abrumadora para sus sentidos (o los de cualquier otra persona). Este consejo es válido tanto si compras para ti mismo como si estás buscando un regalo para otra persona.
Listado top ventas para Aplicaciones para camisetas infantiles
En esta enumeración encontrarás multitud de productos como aplicaciones para camisetas infantiles magníficos para el cuidado de tu salud. En este lugar encontrarás lo mejor para tu cuerpo, comparando entre las mejores marcas y referencias del mercado.

NAGAO Mangas para Brazo Enfriamiento de protección UV,Brazo Deportivo Transpirable Suave y Secado rápido y elásticos Manguitos para Conducir Ciclismo Baloncesto Golf para Hombre Mujere(1Pair A)
- 【REFRIGERACIÓN Y UV 50 PROTECCIÓN】:Con tecnología de refrigeración innovadora y protección UPF 50 para bloquear más del 98% de los dañinos rayos UVA y UVB,mangas refrescantes para el sol NAGAO son más que las mangas solares promedio.
- 【Frescas y Cómodas:】: Fabricadas con materiales frescos de nailon y spandex, estas mangas frescas cambian el caluroso verano para proporcionar una excelente ventilación y comodidad.
- 【Talla única para todo】: Estas mangas de protección solar son universales tanto para hombres como para mujeres, con una gran durabilidad y elasticidad para garantizar que se adapten a todos los tamaños de brazos masculinos y femeninos. Son muy delgados y livianos, sin demasiada presión, pero no se resbalarán.
- 【Amplia gama de aplicaciones】: Tiene una fuerte capacidad de protección de la piel cuando se trabaja al aire libre o se realizan actividades al aire libre.Por ejemplo,golf,ciclismo,pesca, conducción,montañismo,paseos en bote, jogging,jardinería,baloncesto,etc.
- 【Servicio Postventa】: Mangas de hielo deportivas de alta calidad, servicio postventa sin preocupaciones.Si tiene algún problema, póngase en contacto con nosotros, lo abordaremos sin demora, nuestro servicio al cliente profesional y amigable está en línea las 24 horas.


NAME IT Nmfkristina LS Top Box Camiseta de Manga Larga, Amarillo Curry, 98 cm para Niñas
- Camiseta de manga larga para niños con cuello redondo, estampado colorido con aplicaciones 3D en la parte delantera
- Calidad producida de manera sostenible de 100 % algodón orgánico
- Fabricado con algodón orgánico. Este producto está fabricado con algodón orgánico. El algodón orgánico es grown sin el uso de productos químicos nocivos. La granja de algodón orgánico protege los recursos naturales y los granjeros.


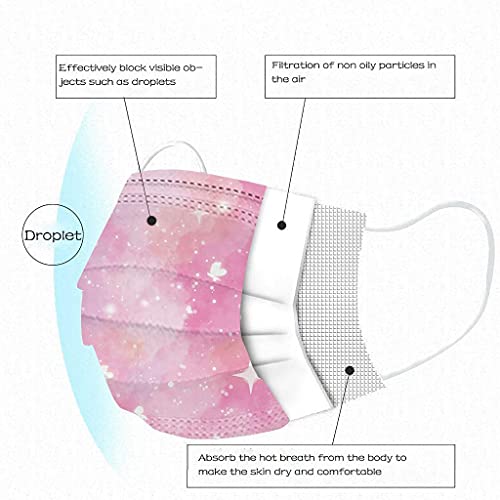
【Entrega rápida - Stock en españa】Fossen 50 Piezas Mascarillas infantil niña niño con Arcoiris Niños, infantil Dibujos Animados,Surtidos para Actividades Aire Libre, Patrón Escuela, Fiesta
- 🧸Mejor protección: Hecho de fibra de poliéster, ecológica, saludable, cómoda y transpirable.La eficiencia del trabajo es superior al 95%, suficiente para adaptarse a actividades al aire libre. 🎒Se puede poner en la Mochilas Escolares Mochila Infantil Regalos Para Niños y Adolescentes
- 🧸Cómodo: Menos resistencia al aire sin afectar el efecto de filtrado, reduciendo la condensación de la humedad y mejorando la comodidad. Cómodo, lo que le permite respirar sin problemas.
- 🧸Aplicabilidad: Adoptando el diseño del puente nasal, se adapta perfectamente al tamaño de la mayoría de las personas y se adapta a casi todas las formas de la cara. Sin irritación de la piel humana, suave, cómodo, insípido, transpirable.
- 🧸Perfecto: Ideal para vuelta a la escuela, actividades al aire libre, ciclismo senderismo y deportes al aire libre. puede proporcionar más protección para exteriores interiores y viajes.Diseño perfecto, mascarilla infantil,mascarillas niños,mascarillas Infantiles,mascarilla Infantil,mascarillas Infantil,mascarilla Infantil
- 🤝 👍 30 días de devolución gratuita: si hay algún problema, no dude en ponerse en contacto con nosotros, le responderemos con prontitud dentro de las 24 horas.Nuestras cuerdas no se desprenden, y si alguna de ellas lo hace, le devolveremos el importe íntegro.


Joma Camiseta Manga Corta Villarreal Amarillo, L
- Se adapta a cualquier actividad deportiva
- Diseño ligero que ofrece comodidad
- Producto adecuado para múltiples ocasiones
- Producto adecuado para actividades deportivas


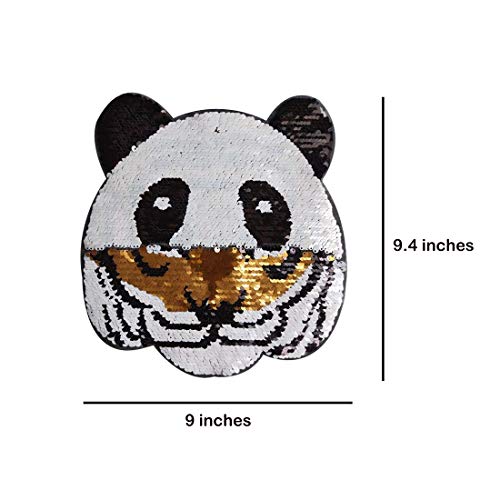
El parche de aplicación de lentejuelas Panda-Tiger se puede cambiar, coser en el parche dos patrones de animales Accesorios de ropa Panda-Tiger para camiseta, falda, pantalones, ropa infantil DIY
- Parche de aplicación de lentejuelas Panda-Tiger, costura convertible en parche de aplicación
- Accesorios de ropa para camiseta, falda, pantalones, gorro, ropa de niños Diy
- El patrón del parche se puede convertir entre panda y tigre al voltear la lentejuela sobre el parche
- Las lentejuelas en la superficie del parche son una forma especial de fijación. Se pueden voltear. Cuando todo esté volteado, el aplique se convertirá en otro patrón diferente.
- Coser en el parche, tamaño aproximadamente 9 * 9.4 pulgadas


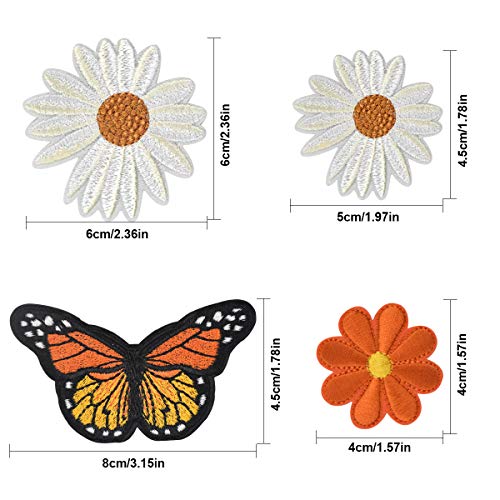
Parches Termoadhesivos Flores y Mariposa Parches Decorativos para Tela Parche para Coser en Ropa Parches Bordados Parche de Ropa para Infantil y Adultos Apliques Patches para Jeans Camisetas Sombreros
- 【Material】 Los parches de aplicación están hechos de tela de poliéster de alta calidad, con formas de flores y mariposas, colores brillantes y patrones exquisitos.
- 【Cantidad】 6 × parches de aplicación (patrón de mariposa) + 8 × parches de aplicación (patrón de flor de sol) + 2 × parches de aplicación (patrón de margarita).
- 【Adecuado para】 Los parches bordados se pueden usar para reparar su ropa, zapatos o sombreros favoritos. También se puede usar para cubrir manchas en la ropa y también se puede usar para decorar diversas artesanías.
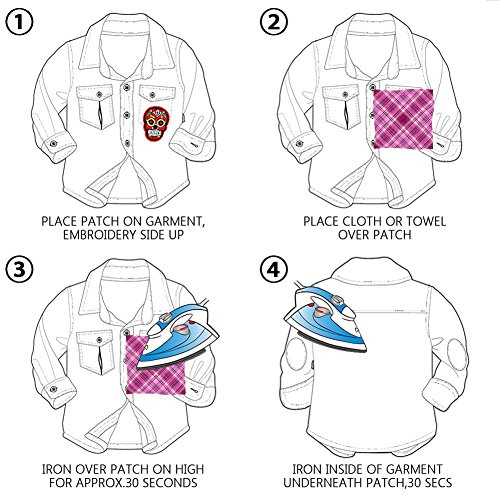
- 【Utilice】 Simplemente coloque el parche de bordado en la ropa, presiónelo con una plancha durante 20-30 segundos. Antes de planchar, asegúrese de que la ropa y las telas sean materiales que se puedan planchar.
- 【Práctico】 Los parches de ropa se pueden usar para decorar chaquetas, jeans, pantalones, camisetas, faldas, mochilas, bufandas, cortinas, sábanas, almohadas, etc. Los colores brillantes y los patrones exquisitos hacen que su ropa se vea más a la moda.


Parche Termoadhesivo Grande - 14.9 x 13.1 cm - Parche para Ropa Infantil Decorativo Bordado Dibujos Animados Animal Vestidos Niñas Apliques para Coser Aplicaciones Termoadhesivas Chica
- MATERIAL SÚPER RESISTENTE: Parche termoadhesivo infantil en material de fácil lavado y resistente a la fricción y al desgarro; la base adhesiva de fusión por calor de ese parche bordado te permite plancharlo a tus prendas de vestir.
- MODO DE EMPLEO: Instrucciones abajo en la descripción del producto.
- PARCHE IMPERMEABLE: Ese parche termoadhesivo se puede lavar a máquina a máximo 30ºC o en frío; no olvides darle la vuelta a la prenda antes de poner la lavadora; por mayor seguridad recomendamos coser el parche.
- IDEAL PARA REPARAR Y DECORAR: Ese parche decorativo es perfecto para personalizar o arreglar las tus prendas y accesorios o las de tu hijo; puedes lucir los parches en jeans, chaquetas, pantalones, sombreros, mantas, mochilas, bolsos, etc.; recuerda que seda, piel y tejidos sintéticos no son adecuados; en esos casos se recomienda coser el parche.
- DETALLES: Motivo; Dibujos Animados; Talla: 14.9 x 13.1 cm; peso: 7 g; material: poliéster bordado.


Parches Bordados, 25 Piezas Animados Lindos Parches Para Ropa Termoadhesivos Infantiles Parches Para Planchar y Coser de Bricolaje Aplicado Ropa Camiseta Jeans
- 💖【Varios Estilos】: Una variedad de opciones, 25 tipos diferentes de lindos parches bordados para niños y adultos, colores brillantes, muy adecuados para la ropa de bricolaje, lo que hace que cada vestido sea único.
- 💖【Adhesión Fuerte】: Hay pegamento en la parte posterior del parches para ropa planchar, que se puede calentar y planchar para derretir el adhesivo especial en la parte posterior. Usamos telas con texturas y colores vibrantes. Puede planchar el parches para tela coser directamente sobre su ropa.
- 💖【Seguridad Del Material】: El parches termoadhesivos planchar aplicado está hecho de una tela que se puede lavar sin decolorarse. Muy suave con la piel, no la rayará y es cómodo para la piel. Y es lavable y duradero.
- 💖【Amplia Aplicación】Puede decorar y reparar perfectamente camisas, jeans, tops, pantalones, chalecos, faldas, etc. Es la mejor opción para que las niñas remenden su ropa.
- 💖【Nota】: El parches para niños de planchado puede caerse porque la temperatura de planchado es demasiado baja y puede repararse planchándolo repetidamente. También recomendamos que cosa el parches bordados después de parches ropa termoadhesivos infantiles colocar mejor el parches ropa en la ropa de los niños.


Parches Para Ropa Termoadhesivos,Rodilleras Pantalones Niños, Planchar En Los Parches Apliques Para Ropa Camiseta Bolsas Pantalon Sombrero Jeans O DIY Coser (32 PCS)
- 【Material】: los parches de aplicación están hechos de nitrógeno de poliéster con colores brillantes y hermosos diseños. Use estos parches para planchar para hacer que su ropa y bolsos sean más atractivos.
- 【Fácil de usar】: Simplemente coloque los parches de bordado en la ropa y presione con la plancha durante unos 20-30 segundos. Antes de planchar, asegúrese de que su ropa y telas sean materiales que se puedan planchar.
- 【PARCHES LAVABLES】: Cada parche es lavable a 40 ° C o menos, se puede lavar a máquina y secar en secadora.
- 【Amplia aplicación】: Ideal para camisetas, faldas, jeans, chalecos, sombreros, mochilas, ropa, cortinas, almohadas, bufandas, edredones, etc. Un regalo para un amigo también es una buena opción.
- 【NOTA】: No se puede aplicar a ningún material impermeable, material plástico o tela o cubierta dura. Puede caerse fácilmente.


Jovi 1410 - Estuche, 12 rotuladores textil, colores surtidos
- Estuche de 12 rotuladores permanentes para tejidos para niños y niñas a partir de 3 años
- Punta tipo pincel de 4,8 milímetros; tapón de seguridad con capuchón ventilado
- Rotuladores base agua; no tóxicos
- Para fijar el dibujo en un tejido dejar secar 30 minutos y planchar durante 3 minutos con el tejido al revés poniendo un cartón o papel para que el dibujo no traspase a la otra cara del tejido
- Resistentes a lavados hasta 40º en ciclo normal de máquina.


FEGIO Parches Ropa Parche para Coser y Planchar 20 Piezas Patch Sticker Cute DIY Ropa Parches para la camiseta Jeans Ropa Bolsas
- ❤ 【FÁCIL DE USAR】 Con adhesivo nano-molecular en la parte posterior, puede plancharlo fácilmente en su ropa. Para hacerlo más fuerte y duradero, cosa algunas puntadas simples después de planchar. Agregaremos una serie de líneas de parche para que le resulte más fácil usar los parches de ropa
- ❤ 【CANTIDAD】 Parche surtido de 20 piezas de poliéster de alta calidad. Cada parche tiene un bordado exquisito y detallado, mano de obra fina, lavable, lavable a máquina y secadora. No solo para niños, sino también para adultos.
- ❤ 【OCASIÓN】 Los parches de ropa son ideales para jeans, chalecos, chaquetas, camisas, bolsos, mochilas, sombreros, toallas, disfraces, capas, mantas, etc. También adecuados para todas las ocasiones, regalos de cumpleaños, Navidad, disfraces de Halloween
- ❤ 【FÁCIL DE LIMPIAR】 Nuestros enlucidos de hierro se pueden limpiar a 40 ° C o menos y permiten lavar y secar en la máquina.
- ❤ 【MULTIFUNCIONAL】 Los parches para diferentes tamaños y diferentes gráficos pueden satisfacer sus diferentes necesidades. Puede hacer que su ropa y accesorios sean más especiales. También puede cubrir agujeros y cicatri


Parches Ropa Termoadhesivos, Gyvazla 32pcs Insignia bordada colorida del remiendo de Coser-En / de hierro, conveniente para las chaquetas de la camiseta de las chaquetas
- 【Gyvazla 32pcs Variedad de parches lindos】 Ofrecen una variedad de selecciones en diseños y formas, no solo para niños, sino también para adultos.
- 【Fácil de usar】 Planchan muy bien sobre algodón y mezclas de pol / algodón, coserlas para hacerlo más sólido.
- 【Personalice su ropa】 No importa si su ropa tiene un orificio por algún motivo desconocido, o si tiene un logotipo que no le gusta, use los parches Gyvazla para cambiarlo a su ropa favorita.
- 【Apto para】 Ampliamente utilizado para decorar y reparar chamarras, camisas, blusas, zapatos, mochilas, sombreros, etc.
- Gyvazla Parches. NOTA: No se puede aplicar a materiales impermeables, materiales plásticos o telas o estuches duros, puede ser fácil caerse.


(5 hojas) Hierro Unicornio para niños en parches, MWOOT Unicornio Calcomanías de Transferencia de Calor con Apliques de Colores para Camiseta Jeans Bolsas Lavables Decoraciones para Fiestas
- Paquete incluido: 5 piezas de hierro de colores en parches sin ropa.
- Amplias aplicaciones: lindo y encantador para todo tipo de prendas. Especialmente indicado para la decoración de ropa infantil, haciendo que la ropa sea más bonita y bonita.
- Gran diversión para los padres: Usted puede optar por usar el hierro de la casa en los adhesivos hechos a mano. Es una gran diversión para usted para la ropa de bricolaje.
- Transferencias de calor respetuosas con el medio ambiente: no tóxicas y seguras, no dañan nuestra piel y son respetuosas con el medio ambiente, lavables y duraderas.
- Fácil de aplicar: use planchas domésticas o máquinas de transferencia de calor, fáciles de usar.


Marabu- Kids Shirt Farbe - Pintura para Camiseta Infantil, 6 x 80 ml, para diseños creativos en Textiles claros, Resistente al Lavado hasta 60 °C, Ideal para niños, Color carbón (0308000000001)
- Contenido: 6 x 80 ml de camiseta KiDS en color amarillo, rojo, azul, verde, rosa y negro.
- Tonos brillantes y luminosos para diseñar telas claras hasta un máximo de 20 % de fibra sintética.
- Fácil de aplicar con brocha, incluso para plantillas.
- El color grueso se puede pintar fácilmente y los tonos se pueden mezclar.
- Se fija en el horno o con la plancha, después se puede lavar hasta 60 °C.


(5 hojas) Bebé de hierro en el parche de transferencia, MWOOT Niños Apliques Surtido Dinosaurio Del Coche Pegatinas de Transferencia de Calor para la Ropa de la Camiseta Jeans Mochila Decoraciones DIY
- Paquete incluido: 5 piezas de hierro de colores en parches sin ropa.
- Amplias aplicaciones: lindo y encantador para todo tipo de prendas. Especialmente indicado para la decoración de ropa infantil, haciendo que la ropa sea más bonita y bonita.
- Gran diversión para los padres: Usted puede optar por usar el hierro de la casa en los adhesivos hechos a mano. Es una gran diversión para usted para la ropa de bricolaje.
- Transferencias de calor respetuosas con el medio ambiente: no tóxicas y seguras, no dañan nuestra piel y son respetuosas con el medio ambiente, lavables y duraderas.
- Fácil de aplicar: use planchas domésticas o máquinas de transferencia de calor, fáciles de usar.


Parche de ropa 32 pcs Decorativos Parches Apliques Termoadhesivos Cute DIY Coser o Planchar para Ropa Camiseta Jeans Sombrero Pantalon Bolsas
- Personalice su ropa: No importa si su ropa tiene un orificio por algún motivo desconocido, o si tiene un logotipo que no le gusta, use los parches Gyvazla para cambiarlo a su ropa favorita.
- Material: Úselo en un tejido bordado que sea ecológico y no sea peligroso para la piel. Si hay agujeros o cicatrices en la ropa, puede usar estos parches para cubrirlos, y los colores brillantes y los patrones especiales los hacen más atractivos.
- Creativo Decoración: Incluyendo 32pcs bordados con exquisita perspectiva y colores brillantes, tamaño différente patches para proyectos de arte hecho a mano. Puede utilizar estos parches para cubrir la parte defectuosa de la ropa o simplemente para la decoración de bricolaje.
- Fácil de Usar: simplemente colocarlos en la ubicación deseada en la prenda y luego pasar una plancha caliente colgar durante unos secondes.Ils no se movió después del lavado de la máquina.
- Amplio Aplicacion: puede ayudarlo a captar la tendencia, nunca detrás de la moda. Ideal para la decoración y la reparación de la camiseta, falda, pantalones vaqueros, chaquetas, sombreros, mochilas, ropa, cortinas, almohadas, bufanda, edredón, etc.

Imágenes de Aplicaciones para camisetas infantiles
Aquí tienes un conjunto de fotografías de aplicaciones para camisetas infantiles para que te hagas una idea y puedas escoger entre todos los tipos de colonia. Pincha con el ratón en una de las fotos para ver la ficha entera del artículo y su coste.