Maquillar cara cuadrada
Un perfume característico, bajo cualquier circunstancia y a cualquier edad, ha de ser intemporal y llevable. Pero, lógicamente, escoger el perfume adecuado para puede ser un desafío con tantas olores en el mercado. Por este motivo aquí te dejamos las mejores como maquillar cara cuadrada, por maquillar o maquillar rojeces. La parte más importante de toda esta ecuación: tu propia nariz. Quieres hallar una colonia que te huela bien de inmediato. Apégate a una olor que no choque con otros olores fuertes y que no sea abrumadora para sus sentidos (o bien los de cualquier otra persona). Este consejo es válido tanto si compras para ti mismo como si estás buscando un regalo para otra persona. El mayor obstáculo para la adquisición de colonias en línea es adquirir un nuevo aroma antes de olerlo. Para ir sobre seguro, ten una idea de qué notas o ingredientes te gustan y cuáles no. Ciertas tiendas proporcionarán una tarjeta de muestra o perfumada con la adquisición para probar primero ya antes de abrir el producto, lo que permite las devoluciones o bien los cambios.
Listado top ventas para Maquillar cara cuadrada
Gracias a esta de referencias queremos mostrarte lo mejor en maquillar cara cuadrada para el confort de tu bienestar. Te aseguramos que podrás encontrar la mejor selección de productos y precios de la totalidad de lo que necesites para tu cuerpo, ofreciéndote la opción de descubrir numerosas marcas y referencias.

Bolsa de cosméticos, Portátil Bolsa de Maquillaje de Viaje, Bolsas de Aseo Cosméticos Neceser de Plegable Multifuncional para Viaje para Mujeres y niñas, Negro
- 【BUENA CALIDAD】La neceser viaje utiliza tela de poliéster de alta calidad, impermeable y resistente al desgaste,sólido y duradero.Además, es muy fácil de limpiar
- 【GANCHO PARA COLGAR】Se diseña con un práctico gancho en su parte superior, que le permite colgarlo en una barra o en la pared de forma más accesible y evitando que se moje en la encimera o en superficies húmedas
- 【BASTANTE CAPACIDAD】La neceser maquillaje es bonito y está bien de tamaño, tiene varios departamentos y colocándolo todo de forma organizada, puedes meter muchas cosas
- 【BOLSOS DE ASEO MULTIFUNCIÓN 】La bolsa neceser tiene dos compartimentos que se pueden desmontar y usar por separado;los bolsillos con cremallera mantienen sus artículos separados y organizados;la cremallera es fuerte, lo que le brindará una mejor experiencia de producto
- 【FÁCIL DE TRANSPORTAR】la neceser de viaje plegable es de tamaño pequeño, liviana y no ocupa espacio,y puede guardarse fácilmente en una maleta, un armario o un bolso,perfecto para guardar sus artículos esenciales de aseo y belleza


HIMRY® Espejo de Baño 8", Regulable en Altura, Aumento 7X para Afeitar y Maquillar, Espejo de Mesa con Doble Cara: 1x y 7X Ampliación, Rotación 360 Grados, 8 Pulgadas, Plateado, KXD3101-7x
- HIMRY Espejo de Baño para Maquillaje o Afeitado, regulable en altura, perfecto para el maquillaje, afeitado y limpieza facial, Perfecto para Regalo.
- Regulable en altura : Espejo de mesa, sería adecuado para cualquier familia, baño, hotel o lugares de lujo en todo el mundo. Cuenta con un cómodo doble espejo de aumento ideal para afeitarse o aplicar maquillaje.
- Doble cara: vista normal 1x y vista aumento 7x. 360 ° de espejo giratorio. Altura ajustable. elegir para ver todos los detalles. Espejo: 17,5 cm ø. Espejo con marco: 20 cm ø, 2 cm de espesor. Color: Plata. Material: metal cromado reales. Hecho de cromo, de fácil limpieza.
- GIRO de 360°: Los ángulos ajustables del espejo le permiten colocarlo en el mejor puesto que le vaya, tanto la cara "normal" como la de 7x aumentos. Además, una vez lo han puesto en el ángulo elegido, no se mueve
- Factura con IVA : TUKAI pagamos impuestos en España y emitimos una factura de impuestos válida. Recibirá automáticamente una factura con el IVA correcto inmediatamente después de que Amazon confirme el envío: como correo electrónico o en el resumen del pedido "Mis pedidos".


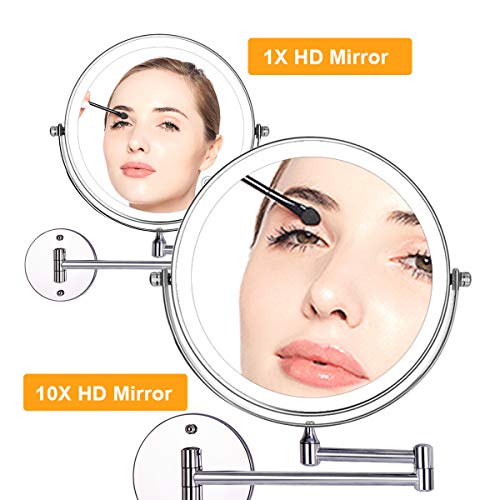
Auxmir Espejo Maquillaje Pared con Luz, Espejo Aumento 1X/10X Doble Cara 360 Giratorio, Espejo Táctil Recargable USB para Baño, Luz Ajustable 3 Colores, Plata
- 👑 AUMENTO 10X PARED: El espejo de maquillaje tiene doble cara, el de aumento 10X completa la necesidad que no se ofrece un espejo normal, como el depilado detallado de las cejas, la pinta de los labios, el afeitado y el uso de lentes de contacto. Este espejo de 10X es perfecto para los que no quieran tanto aumento.
- 👑 GIRATORIO 360° & DISEÑO MODERNO: Se puede instalar fácilmente. Una vez fijado en la pared, no se preocupe por la caída. Este espejo está diseñado con un brazo extensible que puede extender y plegar suavemente. Usted puede ajustar el espejo iluminado a un ángulo de visión preferente personalmente.
- 👑 TRES COLORES DE LUZ & BRILLO AJUSTABLE: Hay 3 modos de iluminación que adapta al entorno con poca luz: luz diurna, amarillo cálido y blanco cálido. Con un toque simple se cambia libremente los 3 modos. Para ajustar la iuminosidad de la luz solo nesecita un toque prolongado.
- 👑 BATERÍA RECARGABLE: El espejo es recargable con un cable USB gracias por la batería recargable, es muy potente, se dura más tiempo. Cuando no lo use, se apaga automáticamente después de 30 minutos.
- 👑 NOTAS: Tiene que acercar su rostro MUY CERCA (aprox. 10 cm) al espejo para ver con claridad. Si está demasiado lejos, verá su cara distorsionada o incluso saldrá boca abajo y puede provocar mareos.


youler Kit de Plantillas de Pintura Facial y Corporal Reutilizables,13 Plantillas de Tatuaje, Escuela, espectáculos, cumpleaños, Halloween, Navidad
- 【CREA ARTE FÁCILMENTE】: las plantillas de tatuajes temporales son adhesivas y extraíbles, lo que te brinda un borde limpio y una posición estable, todo lo que tienes que hacer es elegir el que quieras y pegarlo en tu piel para llenar la muesca. Entonces quítalo, ¡listo! Ayude a su hijo a descubrir y desarrollar sus talentos creativos.
- 【MÚLTIPLES PATRONES】: 13 hojas de plantillas de tatuajes temporales incluyen 104 patrones, combinaciones y opciones creativas casi ilimitadas. Luego, puede crear excelentes diseños con un mínimo esfuerzo; se puede usar con brillo y maquillaje para crear tatuajes temporales. ¡Un verdadero impacto visual! Se ve genial y encantador.
- 【ALTA CALIDAD】: las plantillas de tatuajes autoadhesivas están hechas de PVC blando y son particularmente amigables con la piel. No tóxico que no se puede romper fácilmente, con gran fuerza adhesiva, reutilizable, 100% seguro. Un gran regalo gracias al hermoso empaque, la alta calidad y la cantidad de plantillas.
- 【HAGA FELICES A TODOS】: seguro y divertido para todas las edades, incluidos niños y adultos, y se puede usar en cualquier parte de su cuerpo. Este conjunto te hará lucir diferente, cool y elegante, ¡serás el centro de la fiesta!
- 【MULTIUSOS】 Son pequeños y ligeros. Con varios patrones maravillosos y animados, muy adecuados para reuniones, como carnaval, Navidad, fiesta de cumpleaños, Halloween, representación teatral y mascarada, el color y el brillo no están incluidos en el alcance de la entrega.


ZQO Espejo de Maquillaje Cuadrado, Espejo Plegable Portátil de Doble Cara 1x / 2X Espejos de Bolsillo de Aumento de Mano para Bolsos y Viajes (Negro)
- ★【Exquisita ArtesanÍA】El material ABS y la superficie con recubrimiento hacen que el espejo sea delicado y suave. Los bordes del vidrio son todos bordes y ajustados, lo cual es hermoso y seguro.
- ★【Espejo de Dos Caras PrÁCtico】Un espejo de dos caras adecuado para maquillarse. El espejo primario refleja perfectamente una imagen clara de toda la cara, mientras que el otro lado tiene una ampliación de 2x y es excelente para aplicar rímel, pinzas, depilarse, usar hilo dental, etc.
- ★【Plegable En 180 °】El ángulo se puede ajustar libremente de 0 ° a 180 °, adecuado tanto para la colocación manual como plana. Bien puede satisfacer sus necesidades en diferentes escenarios. Esta es tu herramienta de espejo de maquillaje ideal.
- ★【Ligero y Conveniente】El espejo bolso compacto se puede guardar fácilmente en un bolso o bolso, se puede llevar con usted y también es muy adecuado para usar en el viaje.
- ★【Regalo Ideal】Su alta calidad y su aspecto encantador hacen de este espejo de mano regalo para mujeres de todas las edades en ocasiones especiales (por ejemplo, cumpleaños, aniversarios, etc.) y días festivos.


Fantasia - Espejo de Bolsillo Cuadrado (plástico, Doble Cara, Aumento Normal y 7X, 8,5 x 8,5 cm), Color Blanco
- Aumento de 7 aumentos: los detalles de tu piel, afeitado y peinado. Perfecto para maquillarse, depilar y afeitar. Espejo móvil con bolsillos con marco de plástico sin iluminación.
- Espejo de viaje con ampliación: gracias al tamaño de 8,5 cm, el espejo de mano con aumento cabe en cualquier bolso, cartera, neceser de maquillaje, maletín de maquillaje y bolsa de maquillaje.
- Espejo de maquillaje detallado: el espejo portátil de bolsillo es el espejo perfecto para maquillaje natural y profesional. Los pequeños errores al maquillarse se serán visibles inmediatamente.
- Elegante espejo compacto: espejo cosmético con soporte de plástico blanco (acrílico) para cerrar. El espejo de maquillaje perfecto para viajes. No se pega, colgar, ventosas, etc. Necesario
- Práctico para plegar: pequeño, manejable y cierre magnético. Espejo de maquillaje de doble cara. Espejo doble plegable para que la superficie del espejo permanezca limpia en el bolsillo.


Amelar 8 Pulgadas Espejo Maquillaje de Pared con Luz LED Aumento 1X/10X Espejo Cosmético de Doble Cara con 3 Luces de Colores Recargable por USB, Rotación de 360° Extensible Apto para Baño y Hotel
- ⭐ Espejo Maquillaje Recargable con Luces: el espejo maquillaje tiene una batería de litio recargable de 2000 mAh incorporada que se puede cargar completamente en 2 horas. Por lo tanto, no tiene que considerar reemplazar la batería. Además, el interruptor de control de la luz es un botón de pantalla táctil y el diseño general del espejo cosmético es elegante y hermoso. Es un espejo maquillaje de pared indispensable para ti.
- ⭐ Espejo grande de 8 Pulgadas y aumento de 1X/10X: espejo maquillaje de 8 pulgadas montado en la pared, vista de gran angular, tamaño y proporciones perfectos, más lujoso y elegante. El espejo de tocador tiene un lado doble, un lado es un espejo estándar y el otro lado es un espejo de aumento de 10x que le permite ver sus rasgos faciales claramente y satisfacer sus diferentes necesidades de maquillaje.
- ⭐ 3 Ajuste de Temperatura y brillo de Color: puede ajustar el modo de iluminación y el brillo del espejo maquillaje de acuerdo con el entorno y las necesidades de maquillaje. Presione brevemente el interruptor del sensor para elegir entre luz natural, luz blanca y luz cálida, y presione prolongadamente el interruptor para ajustar el brillo de la luz del espejo de aumento 10x.
- ⭐ Espejo Maquillaje Giratorio y extensible de 360°: varias juntas del espejo maquillaje de pared se pueden girar 360 ° y el brazo flexible se puede extender libremente. para que pueda ajustar el espejo maquillaje al ángulo de visión y la distancia adecuados para que pueda maquillarse, afeitarse, peinarse libremente, etc. Se puede doblar para ahorrar espacio cuando no esté en uso.
- ⭐ Regalo Ideal y servicio al Cliente: el espejo de tocador de pared es un gran regalo para amigos, esposas y madres en cumpleaños, aniversarios, Día de la Madre y Navidad. Si el espejo maquillaje se daña accidentalmente o ya no funciona, no dude en contactarnos. Ofrecemos una garantía de devolución de dinero de 30 días y un año de reemplazo del producto.


Espejo Maquillaje con Luz LED Aumento 1X/10X, Espejo Cosmético Iluminado de Mesa,180 Rotación, Brillo Adjustable Espejo de Tocador Portátil
- 【21 LED Brillantes】FASCINATE espejo maquillaje iluminado está integrado con 21 luces LED ajustables brillantes, le permite maquillarse en diversas situaciones de iluminación como durante el día, la noche, el hogar y la oficina, brillante pero no deslumbrante, protegiendo sus ojos.
- 【Smart Touch Dimmable】Las luces LED se controlan mediante el interruptor del sensor táctil. Una pulsación larga puede ajustar el brillo.
- 【Con Espejo Redondo de 10X Aumento 】El espejo de aumento de 10X desmontable le ayuda a ver cada detalle con claridad y aplicar maquillaje delicado como rímel, delineador de ojos, cejas y lápiz labial. Se pueden montar 2 ventosas espejo sobre cristal o espejo grande.
- 【Fuente de Alimentación Doble】El espejo de maquillaje LED funciona con 4 pilas AA (no incluidas) o cable USB (incluido). El espejo en sí no puede almacenar energía.
- 【Rotación Libre de 180 Grados】Este espejo iluminado se coloca en su encimera y se puede ajustar libremente. Esto se fija en un ángulo de visión perfecto y cómodo. Es un regalo ideal para madre, hermana, esposa, novia, maquilladora, etc.en el Día de San Valentín, Día de la Madre, Navidad, aniversarios u otras ocasiones especiales.


OrgaWise Neceser Maquillaje Impermeable de Gran Capacidad con Gancho Colgante, Viaje Camping Cosas Necesarias, Envía un Lindo Neceser Viaje Pequeño
- COMPARTIMENTOS MÚLTIPLES --- Capacidad grande, tamaño 20 * 25 * 9.5 cm / tamaño expandido 48 * 25 * 9.5 cm, Extra gratis envíe una bolsa con cordón (tamaño 42 * 31 * 21cm). Esta neceser maquillaje es suficiente para contener todos los elementos necesarios, como cosméticos, champú, gel de ducha, cepillo de dientes, toalla, etc. Todo tiene su lugar y puede encontrarlo en un segundo. Hay correas en el compartimiento para mantener los artículos ordenados.
- ALTA CALIDAD --- La neceser viaje utiliza tela de poliéster de alta calidad, tela oxford impermeable y resistente al desgaste, resistente a las salpicaduras de agua del fregadero o la ducha, fácil de limpiar y secar, el compartimiento de PVC y el compartimiento de ventilación de malla protegen sus pertenencias personales contra la penetración o las bacterias , proporcionarle un cuidado personal más limpio y cómodo.
- DISEÑO PROFESIONAL Y PRÁCTICO --- La neceser viaje tiene un asa cómoda, un gancho grueso, bolsillos retráctiles, se puede colgar y doblar. La neceser maquillaje utiliza cierre de cremallera y cierre de velcro, doble seguridad. Cierre redondo con cremallera para una apertura y cierre rápidos y fáciles, libere sus manos.
- PRACTICIDAD --- Hay una tabla dura en el bolsillo principal para dejar, para que la bolsa de cosméticos se convierta en tridimensional y aumente el espacio. La bolsa principal tiene correas elásticas para fijar los artículos, la bolsa principal también tiene un lienzo fijo en ambos lados, que puede contener artículos de tocador grandes.
- PERFECTO PARA VIAJEROS --- La neceser maquillaje es liviana y conveniente, solo tiene 123g, y puede guardarse fácilmente en una maleta, un armario o un bolso. esta neceser maquillaje es muy práctica, lo suficientemente rígida como para permanecer de pie cuando está cerrada, se mantiene plana y recta cuando cuelga.


2000 Piezas de Diamantes de Imitación de Espalda Plana de Vidrio Hot Fix Gemas Cristales Redondas 1,5-6 MM (SS4-SS30) en Caja de Almacenamiento con Pinzas y Bolígrafos de Diamantes(Transparente)
- Material de buena calidad y muy pulido: cada diamante de imitación es brillante y cristal, el pegamento sólido gris grueso en la parte inferior se puede unir a la superficie del objeto muy firmemente por planchado
- Características: tamaño de sección de alta precisión, corte de múltiples caras, trae buena calidad, alto brillo y sin burbujas de diamantes de imitación, cada uno es de alto brillo, alta refracción y superficie de corte brillante
- 6 Tamaños mixtos: viene con 1.5 mm, 2 mm, 2.5 mm, 3 mm, 4.5 mm y 6 mm (artículos pequeños, no para niños menores de 3 años)
- Fácil de usar: estos rhinestones de fijación caliente tienen un pegamento activado por calor en la parte inferior que se funde y se adhiere cuando se aplica calor, haciéndolos súper fáciles de usar; Aplicando pegamento propio y pegándolos a cualquier superficie
- Hierro en pedrería hotfix: aplicar fácilmente con una herramienta de hierro o hotfix para el hogar, puede decorar fácilmente su ropa, bolso, carteras, zapatos, cinturones, teléfonos celulares con estos hotfix de diamantes de imitación

![Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+] Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+]](https://www.iesribera.es/pics/2020/09/16/lampara-de-espejo-aplique-banovitcoco-lampara-led-15w-1200lm-60cm-blanca-fria-6000k-luz-de-maquillaje-con-interruptor-luz-de-espejo-de-bano-impermeab-10313.jpg)
Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+]
- ♔ Potente luz de 15W: esta iluminación de espejo tiene una luz neutra clara, no tiene colores amarillo y azul, con 6000 Kelvin y 1200 lúmenes es muy adecuada como luz de maquillaje. Con un ángulo de haz de 100 °, esta lámpara moderna no deslumbra y el espejo está iluminado de manera uniforme e indirecta.
- ♔ Lámpara de espejo a prueba de agua: esta lámpara de espejo está hecha de aluminio y una pantalla de PC de alta calidad. La carcasa a prueba de salpicaduras cumple con la clase de protección IP44, por lo que la luz del espejo puede funcionar bien en baños u otras áreas interiores húmedas.
- ♔ Diseño moderno y simple: gracias a los cables largos (1,8 m / 5,9 pies), la lámpara se puede usar de manera más fácil y amigable. Solo necesita instalar la lámpara en la pared, luego conectarla con el interruptor incluido. No se requiere cableado adicional y todos los materiales de montaje están en el embalaje.
- ♔ Fácil instalación: el material de montaje es solo un soporte, por lo que esta lámpara se puede usar en diferentes ocasiones debido a su diseño simple. Se puede usar no solo como lámpara de espejo, sino también como lámpara de gabinete o iluminación de cuadros.
- ♔ Ahorro de energía A +: la fuente de luz utiliza un chip de ahorro de energía LED de alta calidad, la carcasa consta de un aluminio mate de alta calidad y una pantalla de PC para PC bien translúcida. No solo ahorra energía y es respetuoso con el medio ambiente, sino que también tiene una larga vida útil.


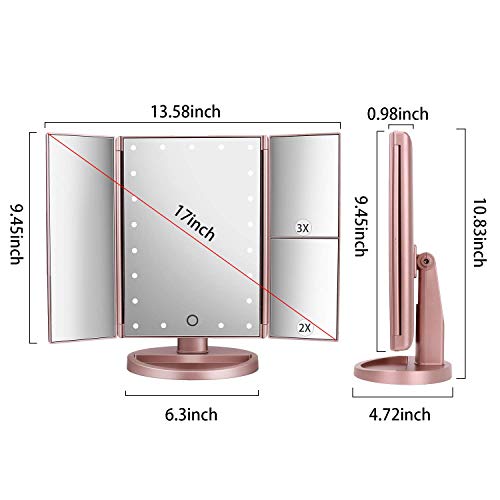
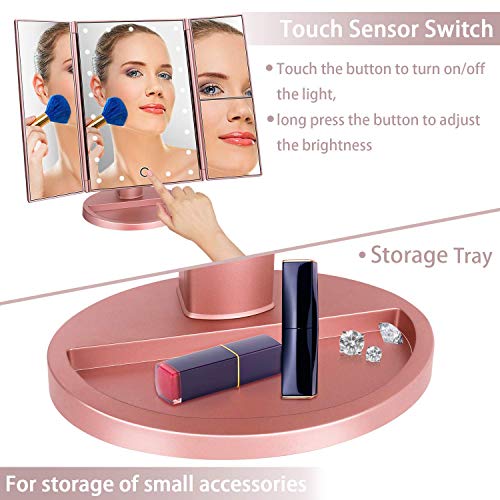
Espejo de Maquillaje con LED, Iluminado Espejo de Mesa Luz con Ampliación 1X / 2X / 3X Plegable Espejo de la Vanidad Rotación 180° Pantalla Táctil Espejo Cosmético para Hombre y Mujer (Oro Rosa)
- 【 21 Luces LED & Interruptor de Sensor de Pantalla 】- La luz es natural y suave, protege sus ojos. Iluminar su cara en condiciones de poca luz. Puede controlar y ajustar la luz por tocar el interruptor táctil en la pantalla.
- 【 Los Modos Dobles de la Fuente de Alimentación 】- El espejo de maquillaje profesional se pueden accionar por la carga del USB o las baterías 4pcs AAA (las baterías no se incluyen, el cable del usb se incluyen). Nota: El espejo no puede almacenar energía por sí mismo.
- 【 Espejo del Maquillaje de Múltiples Funciones 】- Adecuado para hombres y mujeres, por para afeitar de la mañana, cepillando sus dientes, limpieza meticulosa, maquillaje y más. El rebaje de la base se puede utilizar para almacenar lápices labiales, aretes, anillos, collares, relojes, etc.
- 【 Rotación Libre de 180° & Tres ampliaciones 】- Giratorio de 180 °, se puede fijar en cualquier posición según sea necesario. Con el diseño de la ampliación 2X y 3X, vea claramente sus características faciales y los detalles más minúsculos, le ayudan a hacer un maquillaje más perfecto.
- 【Servicio de Calidad 】- Hecho de material ABS de primera calidad, aspecto perfecto y resistencia al rayado. Nuestros productos mejoran el soporte técnico de por vida. Si tiene alguna pregunta o sugerencia, puede contactarnos por correo electrónico.


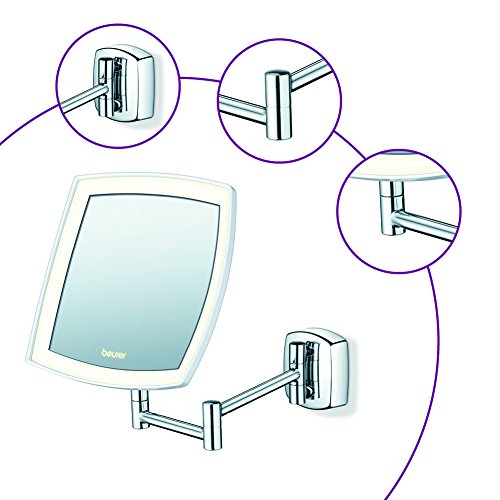
Beurer BS89 - Espejo maquillaje con luz, color plata
- Espejo de pared
- 1 cara vista con aumento (x5)
- Luz LED brillante con 36 LED y 400 Lux
- 3 intensidades de luz
- Alta calidad, acabados cromados: fácil de fijar en pared
- funciona con pilas AA 1,5 V


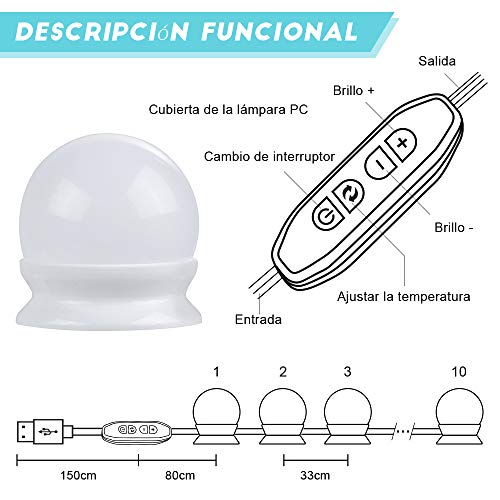
Anpro Luces LED Kit de Espejo con 10 Bombillas regulables,3 Modos Ajustable de Color de Luz,Luz Espejo Maquillaje,Tocador,Espejo,Baño,Regalo para Fiesta,Cumpleaños,Aficionados de Maquillarse
- Este luz de tocador para maquillaje tiene 3 modos de luz (Luz blanca, luz blanca cálida, luz neutra),tiene un botón de control, que se ajusta el brillo de la bombilla según las necesidades reales y seleccionar estos tres colores de temperatura, puede abrir y cerrar la bombilla directamente a través del controlador,es más inteligente y fácil de usar.
- Luz espejo para maquillaje:Se adopta Luz LED de alta calidad, brillo alto, gran ángulo de iluminación, atenuación de luz baja y buena consistencia de color de luz.La bombilla es suave, sin deslumbramiento, sin daños en los ojos, ahorro de energía exquisito y protección medioambiental ecológica.
- El producto viene con una fuerte cinta adhesiva redonda de doble cara, es fácil de instalar y duradera,la longitud total del producto es de 9.8 pulgadas (no icluyendo el adaptador y el atenuador),se puede ajustar la longitud de la línea según sea necesario.
- Se utiliza ampliamente en espejos para el hogar, espejos de maquillaje para espectáculos, espejos para cosméticos, espejos luz para baños,paredes decorativas, salas de exhibición, fotografía, etc. (los espejos no están incluidos)
- Alimentado por un adaptador de salida 5V / 2A / USB, es seguro de usar.Cable transparente de dos hilos + conector USB estándar, puede acoplarse directamente con el adaptador, es fácil de conectar y usar.

Imágenes de Maquillar cara cuadrada
Si quieres elegir de forma visual los productos, aquí puedes ver una galería de fotografías de maquillar cara cuadrada. Pincha una de las fotografías y entrarás a la compra online de perfume en concreto viendo sus propiedades y costo.
















































![Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+] Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+]](https://www.iesribera.es/pics/2020/09/16/lampara-de-espejo-aplique-banovitcoco-lampara-led-15w-1200lm-60cm-blanca-fria-6000k-luz-de-maquillaje-con-interruptor-luz-de-espejo-de-bano-impermeab-10313-2.jpg)
![Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+] Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+]](https://www.iesribera.es/pics/2020/09/16/lampara-de-espejo-aplique-banovitcoco-lampara-led-15w-1200lm-60cm-blanca-fria-6000k-luz-de-maquillaje-con-interruptor-luz-de-espejo-de-bano-impermeab-10313-3.jpg)
![Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+] Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+]](https://www.iesribera.es/pics/2020/09/16/lampara-de-espejo-aplique-banovitcoco-lampara-led-15w-1200lm-60cm-blanca-fria-6000k-luz-de-maquillaje-con-interruptor-luz-de-espejo-de-bano-impermeab-10313-4.jpg)
![Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+] Lámpara de Espejo Aplique Baño,VITCOCO Lámpara LED 15W 1200LM 60cm Blanca Fría 6000K Luz de maquillaje Con interruptor Luz de espejo de baño impermeable IP44 [Clase de eficiencia energética A+]](https://www.iesribera.es/pics/2020/09/16/lampara-de-espejo-aplique-banovitcoco-lampara-led-15w-1200lm-60cm-blanca-fria-6000k-luz-de-maquillaje-con-interruptor-luz-de-espejo-de-bano-impermeab-5.jpg)