Segundo dia rizos
Por suerte los maestros de la fragancia han hecho que descubrir el perfume ideal sea un tanto más fácil que conjuntarlo con la cita perfecta. Tras buscar en los archivos de perfumes algunas de las más populares y también interesantes, encontramos esencias con un probado historial de intriga que han dado sitio a referencias tales como segundo dia rizos, esmalte de unas bourjois un segundo o bien rizos. Depende completamente de nuestros propios recuerdos si un olor nos llega o bien no a la psique, lo que explica por qué razón algunos de nosotros estamos emocionados por un soplo de hierba recién cortada o de gasolina, mientras que otros. No tanto. Considere en qué momento y dónde va a utilizar el aroma. ¿Te va a llevar de la oficina a una futura hora feliz o bien a una cita cuando sea seguro hacerlo nuevamente? ¿O bien es para una circunstancia especial concreta? Quizá prefieras un aroma más atractivo para una cita nocturna, pero una opción más refulgente y relajada durante el día o bien en la oficina.
Listado top ventas para Segundo dia rizos
Gracias a esta de productos queremos mostrarte lo mejor en segundo dia rizos para el confort de tu bienestar. En este momento podrás encontrar lo mejor para tu bienestar, teniendo la oportunidad de comparar entre las mejores marcas y referencias del mercado.

Innovation Cooling LLC IC - Almohadilla térmica de Grafito 40 X 40
- Extraordinaria durabilidad y estabilidad.
- Rendimiento térmico de nivel superior: 35 W/m-k.
- Amplia gama de temperaturas: Rango de funcionamiento: -200 C a +400 C.
- Sólido estado modular: El grafito 100% puro no contiene líquidos por lo que no se puede secar, bombear o hornear como una pasta térmica.
- Reutilizables: La almohadilla se puede reutilizar varias veces sin pérdida de rendimiento.


Buff Tubular Original PINK Unisex Talla única, Gris
- El tubular multifuncional BUFF reinventado: materiales reciclados, protección solar, ultra elástico, sin costuras.
- Tecnología Ultra-Stretch: Ajuste en 4 direcciones, elasticidad superior.
- Diseño específico para niños.
- Disfruta de la versatilidad y las posibilidades de nuestros productos más multifuncionales. Elige entre múltiples formas de vestirlo y posibilidades de protección y estilo.
- Tecnología UltraStretch: máxima elasticidad para mayor rendimiento y comodidad.


Puma Sport Cush Crew 6P, Calcetines Unisex, Paquete de 6, Negro (Black), EU 43-46
- Planta parcial de felpa para una buena amortiguación y una comodidad superior
- Talón y puntera integrados para una mayor sujeción


Schwarzkopf, Blanco, OSIS+ BOUNCY CURLS GEL RIZOS STRONG 200 ml
- SCHWARZKOPF OSIS+ BOUNCY CURLS GEL RIZOS STRONG 200 ml


Kinky-Curly Original Curling Custard - Gel peinador para cabello, 225 g
- Sin crueldad.


Caja giratoria para Relojes automatico Watch Winder Madera de Reloj de Pulsera
- Cajas giratorias: Cajas giratorias para Relojes para guardar el reloj y puede protegerlo del polvo también hace que tu mejor reloj automático luzca cuando no lo llevas puest.
- Funcionamiento silencioso: Este automatico watch winder funcionamiento es muy silencioso,esta caja de reloj de pulsera está alimentada,No use la batería y línea de alimentación al mismo tiempo.
- Fácil de operar: Simplemente presionando el botón de encendido,La caja del enrollador de reloj enrolla automáticamente sus 4 relojes suavemente,gira en sentido antihorario durante 2 minutos primero,pausa durante 6 minutos,luego gire en el sentido de las agujas del reloj durante 2 minutos,pausa durante 6 minutos,luego repita el ciclo
- Compatible con todo: Estuche bobinadora para relojes no importa el tamaño pequeño de las mujeres o reloj de gran tamaño para hombres, la caja devanadera automática de watch winder es capaz de sostenerlo.
- Materiales:Esta Cajas giratoria para relojes fabricado en madera, su interior es de gamuza genial para protección de su reloj,El diseño de la caja de almacenamiento de 6 relojes adicional ahorrará mucho espacioes.


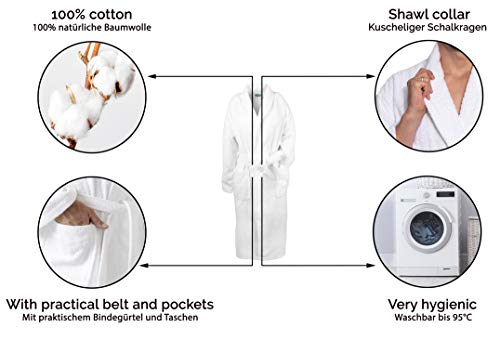
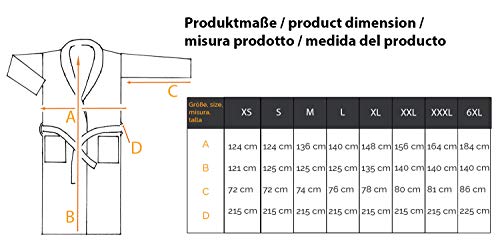
ZOLLNER Albornoz de Ducha para Hombre y Mujer, Talla 6XL, Otras Tallas, algodón
- El albornoz unisex tiene un cuello con diseño tipo esmoquin. Para llevar las llaves u otro objeto que necesitemos, dispone de dos bolsillos laterales. El cinturón permite ajustarlo cómodamente a nuestro cuerpo.
- La bata de rizo le convencerá completamente cuando pruebe su suavidad y su capacidad para secar la piel y librarla del agua después del baño. Además, se seca rapidamente, evitando la aparición de olores.
- Muy resistente a los lavados a altas temperaturas y al uso diario. Se puede lavar a máquina hasta 95° y secar en la secadora. El compañero perfecto para las vacaciones, el gimnasio, el spa, el balneario o la piscina.
- Está disponible en varias tallas, de la XS a la 6XL. El tejido tiene una densidad aproximada de 350g/m². Ha sido elaborado sin emplear sustancias nocivas, como garantiza el certificado Ecotex ( 03.T.3148 Hohenstein HTTI ).
- El elegante y atemporal albornoz blanco tiene un corte amplio y cómodo para ajustarse a todas las figuras. Disfrute en casa de la suavidad envolvente que proporciona su confección en algodón 100%.


Razer Viper Ultimate Ratón inalámbrico para juegos Esports , para gaming, ambidiestro con 69 g de peso, cable Speedflex, sensor óptico 5G con estación de carga, Negro
- Tecnología inalámbrica rápida Razer HyperSpeed: Con una transmisión de gran velocidad, una latencia muy baja y un cambio fluido de frecuencia en los entornos con más ruido, ni te darás cuenta de que están jugando con un ratón inalámbrico
- Sensor óptico Razer Focus+ 20K: Un sensor de 20 000 PPP con una precisión de resolución del 99,6 % asegura que se registre hasta el movimiento más leve del ratón, ofreciéndote un grandissimo nivel de precisión para realizar disparos ganadores y maniobras elusivas
- Peso ligero de 74 g , Diseñado para deportes electrónicos: El ratón Razer Viper Ultimate es el ratón inalámbrico para juegos más ligero, que además aprovecha todo su potencial con su diseño ambidiestro real, su peso óptimo está diseñado para un control más rápido y suave
- Switches ópticos para ratones Razer: Cada clic que haces se realiza a la velocidad de la luz, sin desactivación de rebote, por lo que siempre serás el primero en apretar el gatillo, los switches también duran hasta 70 millones de clics
- Hasta 70 horas de duración de la batería: Una eficiencia energética inalámbrica optimizada hace que funcione a un rendimiento optimo durante hasta 70 horas seguidas: cárgalo una vez a la semana para disfrutar de 10 horas de juego diario


Reebok Freestyle Hi - Zapatillas de cuero para mujer, Negro (Black), 40 EU
- Referencia: 2240.
- Marca: Reebok.
- Talla: 40.


Estelar


El día que se perdió el amor


Educar sin perder los nervios: Guía emocional para transformar tu vida familiar (Libro práctico)

I.C.O.N. India Curl Cream Tratamiento Capilar - 150 ml
- Tipo de Cabello: Cabello Rizado
- Entre sus ingredientes destacamos:
- Quinoa, retiene la hidratación y evita cualquier tipo de fuga.


SYOSS - Espuma Rizos Flex - Rizos Perfectamente Definidos Sin Encrespamiento - 2uds de 250ml
- Espuma fijadora Rizos Flex, consigue unos rizos perfectamente definidos y controlados
- Cuida tu cabello con efecto anti-encrespamiento
- 100% de flexibilidad, se elimina fácilmente con el cepillado
- Ayuda a proteger el cabello del calor del secador
- Pack de 2 unidades


Remington S8590 Keratin Therapy Pro - Plancha de Pelo Profesional, Cerámica, Digital, Keratina, Aceite Almendras, Color Bronce
- El sensor de protección contra el calor proporciona hasta 3 veces más protección contra el deterioro, ofreciendo un pelo 5 veces más fuerte frente a una plancha alisadora convencional sin sensor
- Revestimiento de cerámica avanzada con keratina y aceite de almendras
- Placas flotantes de 110 milímetros para una presión uniforme
- Control digital de temperatura con 5 ajustes entre 160 y 230 °C y función turbo. Calentamiento rápido, lista para usar en 15 segundos
- Elegante neceser resistente al calor, cable giratorio y voltaje universal


Revlon Professional Style Masters Fanaticurls Activador de Rizos Fuertes y Definidos 150 ml
- Activador de rizos
- Protege el cabello de las altas temperaturas
- Control incluso en la humedad y cabellos muy densos
- Proporciona fijación
- Para el cabello: Rizado


Revlon UniqONE, Tratamiento en Spray para Cabello - 150 ml
- Brillo y control del encrespado
- Facilita el peinado y el uso de la plancha
- Repara el cabello seco y dañado
- Efecto desenredante

Imágenes de Segundo dia rizos
Tienes aquí una galería de imágenes de segundo dia rizos para que te formes una idea y puedas escoger entre todos los tipos de perfume. Pincha en en una de las fotos para ver la ficha íntegra del producto y su costo.