Potencia ghd
Entonces, ¿de qué forma escoges el mejor perfume? Suena obvio, pero cuidado con las notas que te dibujan asimismo, por poner un ejemplo, si prefieres una fragancia ligera y fresca, podría valer la pena decantarse por un cítrico o bien un sutil pacto floral. También van a poder encajar en tu búsqueda referencias como potencia ghd, parlux 3500 potencia o bien
Listado top ventas para Potencia ghd
Esperamos que con este inventario de productos encuentres potencia ghd al mejor precio y buena calidad para el bienestar y cuidado de tu bienestar. Te ayudaremos a localizar los mejores modelos, a poder comparar precios y conseguir la mejor opción para tu bienestar.

ghd flight - Secador de pelo de viaje con estuche de viaje edición limitada
- ghd flight - Secador de pelo de viaje con estuche de viaje
- 2 niveles de velocidad y temperatura.
- Potente flujo de aire a una temperatura de 65 °C.
- Boquilla extraíble para un secado más preciso
- Pequeño, con mango plegable.


ghd helios take control now - Secador de pelo profesional con Tecnología Aeroprecís, rosa, Edición 2021
- El secador profesional ghd potente y preciso Take Control Now 2021, en un precioso color rosa en apoyo a la lucha contra el cáncer
- ghd helios incorpora un motor profesional de duración y sin escobillas que proporciona un caudal de aire a 120 kilómetros por hora para un secado profesional en tiempo óptimo
- Secador profesional con revolucionaria tecnología Aeroprecis para un uso intuitivo y un secado preciso; incluye boquilla contorneada de precisión
- Potencia variable y control de temperatura, incluye botón de aire frío; tecnología acústica para un rendimiento silencioso
- Diseño ergonómico y equilibrado; cable de longitud profesional


ghd Helios - Secador de pelo profesional con tecnología aeroprecis, Azul
- ghd helios azul incorpora un motor profesional de larga duración y sin escobillas que proporciona un caudal de aire a 120km/h para un secado profesional en tiempo récord.
- Secador profesional con revolucionaria tecnología Aeroprecis para un uso más intuitivo y un secado más preciso. Incluye boquilla contorneada de precisión.
- Potencia variable y control de temperatura. Incluye botón de aire frío.
- Avanzada tecnología acústica para un rendimiento más silencioso
- Diseño ergonómico y equilibrado. Cable de longitud profesional.


ghd flight - Secador de viaje compacto, plegable, voltaje dual
- Diseño compacto y plegable con boquilla extraíble, voltaje dual y bolsa de transporte incluida
- Configuración de velocidad y temperatura variables para un mayor control durante el secado
- Potente caudal de aire a una temperatura de 65ºc
- Ligero: pesa solo 422g (con cable y boquilla incluidos)
- Tecnología ghd de protección del cabello: se apaga automáticamente cuando se está demasiado cerca del cabello para evitar sobrecalentamiento


Secador de Pelo Profesional Iónico Motor AC 3500W, Secador de Pelo Viaje Cerámica Luz Azul con Difusor y Boquilla Concentradora, 2 Velocidades 3 Temperaturas, Protección Contra Sobrecalentamiento.
- 【Cuidado de cabello de alta tecnología】:Secador de pelo profesional con cerámico , luz azul y los iones negativos pueden hidratar el cabello, mejorar el brillo del cabello y ayudarlo a permanecer antiestático. El infrarrojo de penetración profunda cura el cuero cabelludo, repara el cabello dañado y evita la pérdida de cabello en las primeras etapas.
- 【3500w Potente y resistente】:Secador de pelo profesional iónico con potencia de 3500 watios y AC motor fuerte, consigue un secado de cabello muy rápido y cómodo debido a su poco peso y a su gran caudal de aire. Elige entre sus 3 ajustes de temperatura y sus dos velocidades de aire para crear el estilo y peinado que prefieras, después podrás fijarlo con un toque de su botón de aire frío.Evita el exceso de temperatura y daña el cabello.
- 【Diseño especial】: Este secador de pelo profesional de viaje ofrece 2 velocidaded / 3 ajustes de la temperatura para diversos peinados y tiempos de sequía, así como los ajustes calientes y fríos para diversos tipos del pelo. También con 1 difusor y 2 boquilla concentradora, los dedos del difusor y separa el pelo para traer textura natural, la boquilla se reune el fuerza del viento desde el secador y dispersa el aire con uniformidad apacible.
- 【Diseño humanizado】: Sobre este secador de pelo con difusor, los cables largos de 9 feet/2.75 m le ofrecen un espacio más grande a moverse, nosotros tienen un diseño de la suspensión en el extremo de la cuerda de modo que usted pueda colgarlo en la pared o en alguna parte, el diseño de la manija incluso según principios ergonómicos humanos, fáciles para manejarlo.
- 【Seguridad】:Sistema inteligente de control de temperatura para garantizar la seguridad de su familia. Certificados de calidad CE, GS y RoHS. Si tiene alguna consulta sobre nuestros productos, siempre puede ponerse en contacto con nosotros y estaremos encantados de ayudarle.


ID Italian Design | Secador de Pelo Profesional 3 Modos de Calor, 2 Velocidades de Color Negro - 2200W
- Secador profesional con selector de 3 modos de calor y 2 velocidades | Incluye protección para evitar sobrecalentamiento
- Secador moderno con motor AC de larga duración | 2200W de potencia - Secador con potencia que permite secar el pelo rápidamente y realizar bonitos peinados
- Incorpora un botón de aire frío para fijar el peinado
- Incluye una boquilla concentradora | Secador Negro
- Dimensiones - 25 x 28 x 9,5 cm | Cable de 2m para una mayor comodidad a la hora de secarse el pelo o peinarse | Peso - 390 gr

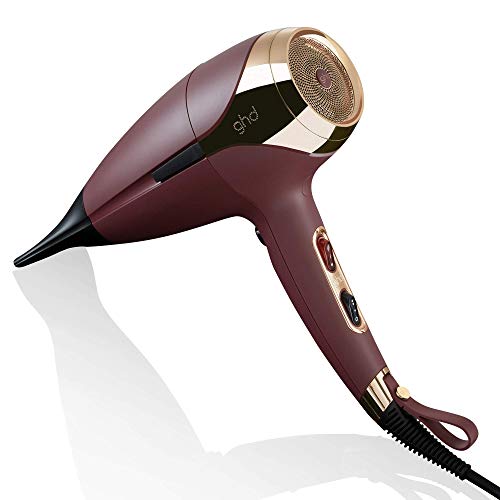
ghd Helios - Secador de pelo profesional con tecnología aeroprecis, Burdeos
- ghd helios burdeos incorpora un motor profesional de larga duración y sin escobillas que proporciona un caudal de aire a 120km/h para un secado profesional en tiempo récord.
- Secador profesional con revolucionaria tecnología Aeroprecis para un uso más intuitivo y un secado más preciso. Incluye boquilla contorneada de precisión.
- Potencia variable y control de temperatura. Incluye botón de aire frío.
- Avanzada tecnología acústica para un rendimiento más silencioso
- Diseño ergonómico y equilibrado. Cable de longitud profesional.


Parlux Advance Light - Secador de Pelo Ionico y Cerámico, color Negro
- Potencia eléctrica de 2200 vatios
- Cuenta con 2 interruptores soft para mayor confort de uso y 3 metros de cable robusto
- Con 2 boquillas: 1 boquilla de 6 cm de ancho y 0.6 cm de alto y 1 boquilla de 7.5 cm de ancho y 0.7 cm de alto
- Accionado del motor K-Advanced con la tecnología cerámica-iónica
- Aire frío instantáneo accionado por micro interruptor
- Menos ruido: silenciador incorporado
- 4 Temperatures
- 2 velocidades
- Respetuoso del medio ambiente : bajo consumo como garantía de medio ambiente sostenible


Remington AC9140 PROluxe - Secador de Pelo Profesional, Secador Iónico, Difusor y Concentrador, 2400 W, Rosa
- Potente secador profesional de 2400 vatios que crea peinados duraderos gracias a la tecnología OPTIHeat; motor de corriente alterna de larga duración y calidad profesional
- Acondicionamiento iónico: 90 % más de iones para reducir el encrespamiento y potenciar el brillo
- Ráfaga de peinado perfecto: optimiza la temperatura y dirige el calor allí donde se necesita. 3 temperaturas, 2 velocidades y ráfaga de aire frío real
- Incluye difusor y concentrador avanzado de 7 milímetros
- Dispone de rejilla trasera desmontable para una limpieza fácil, gancho para colgar y cable profesional de 3 metros


ghd Air Kit - Secador de pelo profesional con tecnología iónica, difusor, cepillo cerámico y 2 clips ghd, color negro
- ghd air kit es un kit de secador para conseguir un secado profesional sin salir de casa
- El kit lo componen el secador profesional ghd air con boquilla de precisión, el difusor ghd air, el cepillo cerámico radial numero 3 de ghd y dos clips de secciones
- ghd air: secador de pelo con potente motor AC 2100W y tecnología iónica para un secado de peluquería rápido
- Secador de diseño ergonómico tanto para diestros como para zurdos
- Cable de 3 metros y enchufe Europeo
- Enchufe Europeo


ghd air - Secador de pelo profesional con tecnología iónica
- El secador de pelo profesional ghd air cuenta con control de temperatura y velocidad variable.Botón de aire frío
- Potencia profesional del secador de 2100W y de Motor AC 240v
- Diseño ligero y ergonómico apto para diestros y zurdos
- Incluye una boquilla de aire para un secado más rápido y un alta precisión
- Cable de 3 metros
- Enchufe Europeo


Termix 000599 Wild - Plancha de pelo con tecnología iónica, de cerámica y turmalina, regulador de temperatura, potencia máxima de 240w, neceser teddy térmico incuido.
- La plancha Termix profesional wild está especialmente pensada para aquellos que quieren conseguir tanto un alisado perfecto, como unas ondas salvajes
- Apagado automático: A los 60 minutos de inactividad, la plancha profesional WILD se apagará de forma automática, para evitar descuidos y un consumo de energía innecesario.
- Gracias al nuevo diseño extralite y a sus placas basculantes, la plancha permite un dominio más rápido y ligero del cabello
- Cerámica y turmalina iónica: Las placas de la nueva plancha WILD incluyen cerámica y turmalina para un acabado mucho más brillante.
- Además, sus propiedades iónicas permiten controlar el encrespamiento para cabello pulido por más tiempo.
- Regulador de temperatura: Permite regular la temperatura en 5 posiciones entre 150ºC y 230ºC con tan sólo un clic. De esta manera, podemos adaptar el calor al tipo de cabello para asegurar la máxima protección y el mínimo impacto.
- Potencia: de 110 a 240w
- Neceser teddy: La nueva plancha de pelo Profesional WILD no llega sola. Sino que lo hace acompañada por un protector de silicona para las placas y un neceser térmico a prueba de altas temperaturas recubierto de un suave pelo.


Rowenta Infini Pro Elite CV8722E0 - Secador motor profesional AC 2200 W, función Ionic, boquilla concentradora de 8 mm y difusor, 2 velocidades y 3 temperaturas, botón de aire frío
- Motor Profesional AC con 2200W de potencia, preparado para soportar largas sesiones de peluquería manteniendo siempre un rendimiento óptimo
- Boquilla concentradora de aire de solo 8 mm y difusor incluido para adaptarse a tu peinado
- 2 velocidades y 3 selectores de temperatura; incluye botón de aire frío para fijar los peinados y aumentar la durabilidad de los mismos
- Función Ionic: genera iones negativos que neutralizan la electricidad estática del cabello y le proporcionan brillo
- Anilla de sujeción y cable de 1,8 metros para mayor comodidad durante las sesiones de secado y moldeado
- Rejilla extraíble para una limpieza sencilla que ofrece un rendimiento de larga duración


ghd original - Plancha de pelo profesional, tecnología cerámica
- Plancha de pelo profesional para pelo largo, corto o media melena; permite crear looks lisos, ondas y rizos
- Tecnología de calor: esta plancha de pelo ghd incorpora un sensor cerámico que garantiza una temperatura óptima de peinado de 185 grados C de raíces a puntas
- La styler ghd Original incorpora placas contorneadas y basculantes: consigue un peinado más rápido, sin encrespamiento y con más brillo
- La ghd Original alcanza la temperatura óptima en tan solo 30 segundos
- Lleva tu plancha ghd a cualquier parte del mundo gracias a su voltaje universal
- Enchufe Europeo


Remington S8540 Keratin Protect - Plancha de Pelo, Cerámica, Digital, Keratina y Aceite de Almendras, Resultados Profesionales, Marrón Oro
- Placas con revestimiento de cerámica avanzada con keratina y aceite de almendras
- Control digital de temperatura con 9 niveles entre 150 y 230°; calentamiento rápido, lista en 15 segundos
- Placas flotantes para uniformizar la presión sobre el cabello
- Ajuste Pro+ para un peinado más sano, función turbo y función de bloqueo de temperatura
- Neceser resistente al calor incluido, cable giratorio. de 1,8 metros y voltaje universal

Imágenes de Potencia ghd
Aquí puedes ver una agrupación de fotografías de potencia ghd para que te formes una idea y puedas seleccionar entre todos los modelos de perfume. Pincha con el ratón en en una de las imágenes para ver la ficha entera del artículo y su costo.




































































