Diferentes tipos de cabellos
La olor, tras todo, es de forma profunda personal. Para la mayor parte, la fragancia tiene el poder de convocar recuerdos, de ahí que ciertas novias optan por un perfume especial, separado de su firma diaria, para el día de su boda. Mas la fragancia asimismo puede ayudar a convertirte en quien deseas ser. Y eso es exactamente lo que estos sets de perfume o bien otros productos como diferentes tipos de cabellos, diferentes tipos de gafas de sol o diferentes tipos de trenzas ofrecen. Cómo se huele dice mucho sobre quién es uno, especialmente en un planeta donde las primeras impresiones ahora significan todo. Algunas personas escogerán un fragancia diferente toda vez que compren un nuevo frasco, a ciertos les puede agradar adherirse a una etiqueta en particular, e incluso hay quienes escogen una fragancia por siempre - un olor que sienten que los define como persona. Es esencial no utilizar perfume o productos corporales perfumados cuando se compra una nueva olor, en tanto que esto puede trastocar el desarrollo de la fragancia elegida.
Listado top ventas para Diferentes tipos de cabellos
Con esta de artículos vamos a mostrarte lo mejor en diferentes tipos de cabellos para el bienestar de tu bienestar. Toma conocimiento de que para encontrar sinfín de opciones para comprar lo mejor para tu salud, te encuentras en uno de los mejores sitios web de la red.

Pack de 12 bobinas de pelo trenzadas para diferentes tipos de cabello, rizado, largo o corto.
- Buena elasticidad: estas bandas de pelo tienen buena elasticidad, no perderán su tamaño original después de estirarlas y se pueden reuse
- Regalo perfecto: estas bandas de goma trenzadas vienen en tres colores hermosos y son perfectas como regalo de cumpleaños para tu amigo, hija, mirada o madre
- Alta calidad: estas bandas de goma trenzadas están hechas a mano de material de alta calidad y tienen buena elasticidad. Es suave y duradero, fácil de llevar, mantiene tu cabello bien y no daña tu cabello, seguro y cómodo
- Amplia aplicación: esta cinta de pelo trenzado es adecuada para todo tipo de estilos de cabello, y es flexible y puede mantener tu cabello firme. Adecuado para diversas ocasiones como la escuela, la oficina o para el trabajo, los deportes o los juegos. No tienes que preocuparte de que el pelo se estropee cuando lo lleves durante el entrenamiento
- Lo que obtienes: recibirás 4 bandas de pelo trenzadas de color azul claro, 4 bandas de pelo trenzadas rosas, 4 bandas negras para un total de 12 bandas trenzadas, tiene un diámetro de 5 cm


Cepillo para el cabello, plancha y rizador de cerámica profesional 2 en 1, herramienta de peluquería con rizador eléctrico con indicador de temperatura, para diferentes tipos de cabello
- ★ Cerámica de turmalina: conducción de calor de turmalina, velocidad de calentamiento rápida, reducción de daños por calor en tu cabello, te ayuda a eliminar problemas de quemadura, le da a tu cabello un aspecto suave y sedoso, natural.
- ★ Diseño de doble uso: se puede utilizar tanto como plancha de pelo como rizador. Doble uso en húmedo y seco, evita problemas de burbuja en seco, más cómodo y práctico.
- ★ Buen rendimiento de temperatura – te ayuda a crear peinados elegantes y atractivos sin necesidad de un estilista.
- ★ Indicador de temperatura - Evita el sobrecalentamiento para dañar el cabello, más intuitivo y claro.
- ★ Tipo de cabello aplicable: adecuado para todo tipo de cabello: grueso, fino, fino, ondulado, rizado o encrespado. Adecuado tanto para peluquería profesional como para uso personal.


3 Piezas Cepillo de Pelo peine peluqueria peine de corte profesional cepillo pelo jabali cepillo antiencrespamiento para Mujer Hombre Diferentes Tipos Pelos
- Materiales de alta calidad: los productos están hechos de materiales de nailon de alta calidad, sin olor peculiar, para garantizar la durabilidad y la no deformación, al mismo tiempo que son livianos. Deslízate sobre cualquier peinado fácilmente sin tirones ni rasguños.
- Efecto de masaje: cada cerda del cepillo curvo con ventilación tiene una punta esférica. La punta esférica produce un efecto de masaje en el cuero cabelludo al peinar el cabello, estimula la circulación del cuero cabelludo, promueve el crecimiento del cabello y ayuda a mantener el cuero cabelludo y el cabello saludables.
- Diseño antideslizante: el peine para cortar el cabello adopta un diseño antideslizante y tiene una sensación de agarre total. El mango se adapta cómodamente a la mano para evitar que se caiga cuando se usa.
- Secado más rápido: menos tiempo de secado equivale a un cabello más saludable. El peine para cortar el cabello está ventilado y se puede secar más rápido con un secador de cabello. Las rejillas de ventilación permiten el flujo de aire a través de todas las partes, calientan el cabello de manera uniforme, reducen el tiempo de secado y evitan que el cabello se dañe por sobrecalentamiento.
- Amplia gama de usos: el peine para cortar el cabello es adecuado para cabello húmedo o seco, cabello largo o corto, cabello fino o grueso, cabello liso o rizado. Es un salón profesional de corte, tinte y peluquería. Un artículo imprescindible para peluquerías.


48 Piezas Rodillos para El Cabello, Rodillos para El Cabello Herramientas para El Cabello, Sin Daños para El Cabello, para Diferentes Longitudes y Tipos de Cabello
- 🎀Material: Se pueden llevar rulos para el cabello hechos de material de nylon, con excelente calidad y rendimiento, reutilizables y livianos, lo que ayuda a crear un hermoso cabello ondulado.
- 🎀Fácil de aplicar: los rulos para el cabello pueden permanecer solos en su cabello sin alfileres. No es necesario usar electricidad, operación simple, agarre cómodo, crear rápidamente la forma ideal de cabello rizado, puede rizarlo solo en el tiempo libre.
- 🎀Diseño único: Hair Rollers está diseñado con un clip de resorte, es muy estable y no se caerá como otros clips. Sin daños químicos en su cabello.
- 🎀Clip de pico de pato: recibirá 12 piezas de clips de pico de pato para que arregle su cabello, están empaquetados al azar de púrpura, rosa, azul, naranja, amarillo, verde, rojo, rojo claro; combina bien con su autoagarre rulos, ayuda a completar muchos peinados.
- 🎀Versátil: Hair Rollers es adecuado para cabello largo o corto con diferentes texturas, puede cambiar su estilo de cabello todos los días, una excelente opción para uso doméstico o de peluquería, excelentes regalos para niñas y mujeres.


Moldeador Dyson Airwrap Complete Styler para diferentes tipos de cabello y estilos, color fucsia
- Dyson Airwrap Volume + Shape Styler - para cabello fino y plano: – Barricas Airwrap de 1,2 pulgadas – Diseñado para crear rizos voluminosos o ondas.
- - Cepillo suave para alisar el cabello fino.
- - Cepillo voluminizador redondo diseñado para dar volumen y dar forma al cabello fino y plano.
- - Secador de pelo prepeinado: lleva el cabello húmedo a húmedo, para preparar el peinado.
- - Dyson Airwrap Base - Estuche de almacenamiento - almacena perfectamente tu Dyson Airwrap Styler y sus accesorios.


Qagazine Diadema para mujer, diseño de moño de tela, estilo bohemio, para mujer, diseño simple, hermosa, para el cabello, accesorios para mujeres, niñas, diferentes tipos de cabello
- Nuestras hermosas diademas son perfectas para el uso diario casual, o para vestir un atuendo formal para una próxima celebración o noche en la ciudad con amigos.
- Nuestros accesorios elásticos para el cabello son suaves y suaves, no se rompen fácilmente, son cómodos de llevar y no dañan tu cabello.
- Son adecuados para niñas y mujeres para llevar en diferentes ocasiones como la vida diaria en interiores y exteriores, como fiestas, ceremonias de boda, conciertos, cumpleaños.
- Es un gran regalo para cualquier persona a la que amas en Navidad, Año Nuevo, cumpleaños, día del profesor, día de la madre, día de San Valentín, etc.
- Este aro de pelo es un buen ayudante para tu maquillaje y fácil de hacer tu propio peinado.


SJKAONJJKAI 4 Piezas Horquilla Rectangular Pinzas para El Cabello Medianas Grandes Pinzas Cabello Retro Pinza De Pelo Acrílico para Cabello Medio-Largo, Cabello Largo Y Diferentes Tipos De Cabello
- 💚Duradero: la pinza para el cabello está hecha de material acrílico, que es duradero y no es fácil de romper. La superficie lisa puede mantener un color permanente y evitar que el patrón se desvanezca.
- 💚Diseño retro clásico: las horquillas de estilo retro se ven particularmente elegantes. El color puro es muy atmosférico y simple, muy adecuado para su atuendo diario y ocasiones especiales.
- 💚 Diseño antideslizante: la pinza para el cabello automática simple adopta un diseño curvo clásico y está equipada con un resorte fijo, que puede fijar su cabello en su lugar y garantizar que la pinza para el cabello no se salga fácilmente.
- 💚 Pinzas para el pelo de diferentes colores: con 4 pinzas para el pelo de diferentes colores, aptas para cabellos largos. Se pueden decorar diferentes tipos de ropa, colores de cabello y peinados para mujeres y niñas.
- 💚 Amplia gama de usos: adecuado para una variedad de tipos de cabello, adecuado para cabello largo. Es ampliamente utilizado para fiestas, trabajo, viajes y uso diario.


18 unidades de diferentes tamaños de perlas,U tipo de pinzas de pelo de perlas de moda,Elegante boda de compromiso fiesta novia pelo tocado adorno perla pelo pin
- --Elegantes horquillas de plata de perlas artificiales de tamaño mixto de tamaño mixto, hermosa joyería para el atuendo cuando asiste a una fiesta, un banquete de cena o boda para mujeres, novia, dama de honor.
- --Alfileres de pelo de perlas mixtas de alta calidad, estilo U, simulación elegante perla, horquillas de aleación chapada en plata, no se oxida y no se decolora.
- --Los pines de perlas artificiales mezcladas longitud total de aproximadamente 7,5 – 7,8 cm, longitud de pin tipo U alrededor de 6,5 cm, total 18 piezas de perlas mezcladas para el pelo de tamaño de los horquillas para el cabello.
- --El buen consejo de mantenimiento de las horquillas de perlas es evitar usar las horquillas mientras se baña o dormir, y colóquelas en el joyero cuando no las use.
- --Moderno, encantador y atractivo. Adecuado para llevarlo en cualquier ocasión como bodas, cenas de San Valentín, aniversario, graduación, graduación, carnaval, banquete o una fiesta en particular.


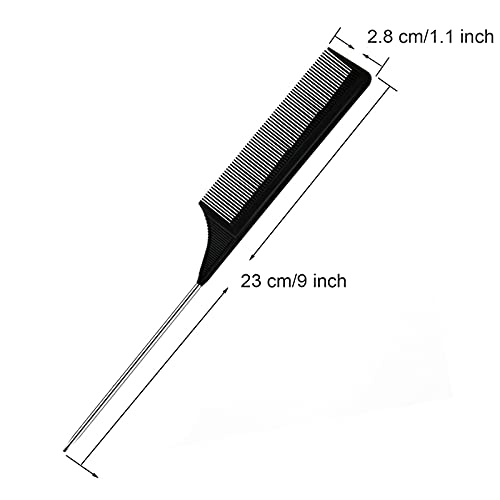
Peine de cola de rata, peine de pelo profesional para resaltar, corte de pelo antiestático para peluquería de salón y para hombres y mujeres con diferentes tipos
- 【Diseño especial】Peine de coloración extra largo con paleta antideslizante, que puede deslizarse suavemente en su cabello sin causar dolor a su cabello y cuero cabelludo. Los dientes espaciados adecuados del peine podrían ayudar a agarrar y separar el cabello con un mango cómodo a prueba de deslizamiento para sostener.
- 【Features】Cree cualquier estilo que le guste con el peine de cola de rata para seccionar y peinar. De tamaño especial para todas las necesidades de corte. Diseñado con un paso gradualmente decreciente para facilitar una tensión uniforme en el cabello. El clip tiene múltiples dientes, lo que puede aumentar la fricción en el cabello y el clip, no es fácil de deslizar.
- 【Heat-resistant & Anti-static】Estos peines metálicos de cola de alfiler son producidos por el plástico con la aguja antiestática y de acero-son ligeros, duraderos y pueden soportar el calor extremo. Los dientes del peine no dañarán la cabeza, lo que ayuda a prevenir el pelo suelto y encrespado durante el peinado.
- 【Fácil de Operar】Como usted peina a través de una sección del cabello, parte del cabello estará en los dientes superiores y parte estará en los dientes inferiores, a continuación, deslice su dedo entre la sección superior e inferior agarrando sólo el pelo en los dientes superiores que será muy bien seccionado para usted. peine de pelo de tejer puede ayudar a acelerar el tinte y el estilo para hacer su peinado se ve mejor.
- 【Practical Field】El peine de corte de pelo adecuado para el cabello de la mayoría de las personas, incluyendo el pelo liso, húmedo y rizado. El mango puntiagudo de la cola se aplica para dividir la línea del cabello y rizar el cabello, lo que le ayuda a cuidar el estilo de forma rápida y eficiente.


3 piezas Peines de Cola de Rata Peines con Pintail de Acero Inoxidable Peine de Separación,peluquería Peine para Mujer Hombre con Diferentes Tipos de Pelos(Negro)
- Combinaciones agradables: recibirá 3 piezas de peines para el pelo de cola de rata, combinaciones agradables para sus necesidades de peinado, el peine para el pelo de la cola de rata presenta dientes finos y mango de acero inoxidable, bueno para seccionar, peinar y separando tu cabello.
- Material estable: estos peines pintail están que es liviano y flexible para operar, con buenas características resistentes al calor, estables y no fáciles de romper, pueden funcionar con su secador de pelo lo suficientemente duraderos para su uso prolongado.
- Diseño práctico: nuestro peine de separación se ha diseñado con un mango largo y delgado de acero inoxidable, que es adecuado para seccionar, teñir el cabello, dividir líneas, separar y peinar, creará peinados diferentes pero hermosos para usted, fuertes y firmes, el mango no es fácil de deslizar y fácil de operar.
- Cómo utilizar: Terminación púa perfecta para proteger el cuero cabelludo. Profundiza fácilmente en las capas inferiores del cabello. Utilice los dientes finamente espaciados y estándar espaciados para agarrar y separar el cabello con el fin de llevar a cabo mejor corte de pelo, morir el cabello y otros trabajos.
- Función: fuerte y flexible; Los peines burlones no se romperán durante el uso normal, agregarán brillo y brillo al cabello opaco; Dientes de longitud alterna con bordes dentados que son buenos para provocar el cabello, adecuados para kits de salón.


Nintendo - Figura Amiibo Zelda Scholar Serie Zelda
- Tipo de producto: figura interactiva
- Plataforma del juego: Nintendo Wii U, Nintendo 3DS, Nintendo Switch
- Es la figura Amiibo Zelda Scholar perteneciente a la Colección Zelda
- Es un regalo adecuado en cualquier momento


Lunario 2020: Calendario lunar para el huerto


Tratamiento para el cabello maltratado: Síntomas, causas, tratamiento y remedios naturales para los diferentes tipos de cuero cabelludo


Paquete de 3 Lilywoods cepillo de pelo de alta calidad - cerdas de jabalí + madera + pincel fino diferentes tipos de cabello
- Hecho con materias primas de alta calidad
- Contiene un cepillo de madera para el pelo rizado y también se puede utilizar como un masajeador del cuero cabelludo
- Incluye: cepillo facial exfoliante + cepillo de pelo de viaje con cojín de goma, alfileres blancos y cerdas puras de jabalí + mini cepillo de pelo de viaje con cojín de goma y alfileres blancos
- Regalo perfecto para las señoras para los días de fiesta que vienen


N.2 La Isla De Tia Lola (Cuentos de Apoyo. serie Roja) - 9788431629557

Imágenes de Diferentes tipos de cabellos
Te mostramos aquí una serie de imágenes de diferentes tipos de cabellos para que te hagas una idea y puedas seleccionar entre todos los tipos de perfume. Pincha con el ratón en en una de las fotografías para ver la ficha íntegra del artículo y su coste.