Aplica dry
Existen muchos perfumes en el mercado y en cualquier tienda de venta al público en línea. No obstante, no se puede estar seguro de su longevidad y calidad. Dale una ocasión a referencias tales como aplica dry, cuando se aplica el iluminador o bien
Listado top ventas para Aplica dry
En esta enumeración puedes comprar numerosos artículos como aplica dry magníficos para el cuidado de tu bienestar. Toma conocimiento de que para encontrar infinidad de opciones para obtener lo mejor para tu cuerpo, estás en uno de los mejores sitios web del mercado.
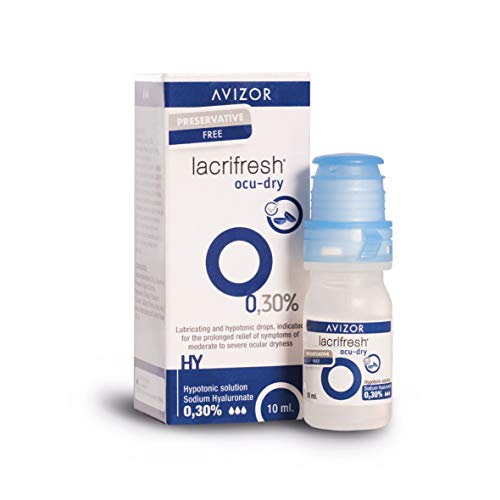
Avizor Lacrifresh Ocu-Dry 0.30%. Frasco de 10ml de gotas oculares para aliviar los síntomas de la irritación ocular.
- Formuladas con un componente activo presente en el ojo de forma natural: ácido hialurónico (0,2%), que aporta un confort adicional y más duradero en el tiempo
- Con hialuronato de sodio 0.20% de alto peso molecular más glicerina y povidona; avizor lacrifresh ocu-dry 0.30%
- Indicado para su uso con o sin lentes de contacto; frasco de 10ml de gotas oculares para aliviar los síntomas de la irritación ocular
- Ofrecen una duradera humectación y lubricación del ojo
- Alivio de la sequedad ocular leve o moderada


T. Leclerc Sombra De Ojos De Aplicación Wet and Dry 2,5 G


ARGANICARE Champú Macadamia For Dry & Damaged Hair 400 ml
- Aplicar sobre el cabello húmedo.
- Masajear el cuero cabelludo con suavidad.
- Hacer espuma.


Alfaparf, Cuidado del pelo y del cuero cabelludo - 150 ml.
- Alfaparf Style Stories Blow Dry Cream (Crema Seca) 150 ml


Ranger Inkssentials Cut-N-Dry - Almohadilla Recortable de Espuma para aplicar Tinta, Color Blanco
- Ranger Inkssentials Cut-N-Dry Stamp Pad Foam
- 8''x10''


Finish Line no Goteo Cadena Luber
- Lubricar cadenas sin a gota
- No varios golpes/verdrecken del entorno o la rueda
- Consume 50% menos de cadenas (alrededor de 3 ml por aplicación, kit contiene 120 ml cadenas)
- Ahorra tiempo
- De contiene cierre de transporte y dos almohadillas adicionales de lubricar una cadena en pocos segundos de cada pad puede utilizarse al menos 25 veces


Naturls Cepillo para el cuerpo – Cepillo de cobre con caja de regalo de hierba de alta calidad – Cepillo de madera de haya FSC – Fabricado en Alemania – Dry Brush con aplicación y consejos de cuidado
- ⚡️EL ENERGIZADOR DE LAS MUFLAS DE LA MAÑANA: ¿Tú también lo sabes? Dificultad para levantarse de la cama por la mañana y cansancio permanente durante el día. ¡Ponle fin ahora y empieza con nuestro cepillo energético!
- 🌬 REAFIRMANTE CONTRA LA CELULITIS: Cepilla a diario para una piel joven y firme. Nuestro cepillo de cobre a menudo tensa la piel después de unos pocos usos y te hace lucir joven y fresca.
- 🌷DESINTOXICACIÓN Y DRENAJE LINFÁTICO: Promueve la desintoxicación de tu cuerpo - El cepillado diario con tu cepillo corporal estimula la circulación sanguínea y estimula tu sistema linfático. ¡Esta desintoxicación natural puede incluso aliviar el dolor!
- 🎁 DA CONFIANZA A TUS SERES QUERIDOS: La piel flácida a menudo conduce a una falta de confianza en sí misma en muchas mujeres, ¡que puedes aumentar nuevamente con nuestro cepillo seco!
- 🇩🇪FABRICADO EN ALEMANIA, SOSTENIBLE Y NATURAL: Nuestro cepillo de monasterio está hecho con amor y se compone únicamente de materiales naturales como madera de haya FSC, alambre de cobre ultrafino y crin de caballo, lazo de cuero de alta calidad. Tú también puedes apoyar nuestra pequeña empresa familiar con una compra


Full Dry Volume Blast 238ml


Triple Dry Carbon - Desodorante antitranspirante roll-On de 50 ml para evitar la sudoración intensa, con carbón activo para 72 horas de protección segura, antibacteriana, antitranspirante, 50 ml
- Eficaz protección contra el sudor fuerte: el desodorante ofrece una protección fiable contra los olores corporales con una fuerte transpiración y un estilo de vida activo, con su fórmula especial de triple acción y carbón activo, y garantiza que los hombres siempre tengan una sensación de piel segura y seca.
- Potente acción: el antitranspirante antibacteriano no solo combate el olor corporal, sino también la sudoración y reduce los poros de sudor, lo que reduce las emisiones de humedad y las bacterias que causan mal olor.
- Aplicación: para un efecto óptimo, el antitranspirante se aplica sobre la piel por la noche antes de acostarse, por lo que la fórmula activa puede proporcionar una alta protección durante la noche y proporciona 72 horas de seguridad y sequedad.
- Aroma fresco y masculino: una vez que la transpiración está bajo control, la aplicación solo tiene que hacerse 3 veces a la semana, para que siempre se mantenga fresco y fresco en la carretera o en el día ajetreado, el desodorante tiene un aroma fresco y masculino.
- Contenido del paquete: 1 roll-on antitranspirante de carbono de 50 ml contra la sudoración fuerte de Triple Dry.


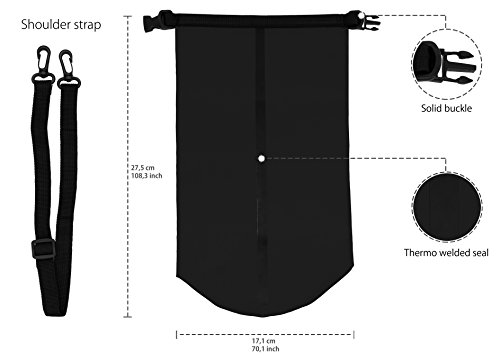
MyGadget Bolsa Estanca 2L - Bolsa Impermeable - Dry Bag Protección Waterproof Mochila para Viajes y Deportes cómo Kayak, Surf - Negro
- SU PRODUCTO - Una practica bolsa seca ultraligera, grande, resistente al agua, que mantiene sus artículos personales, cámara, móvil, ropa, llaves siempre protegidos sin temor a que se mojen. Esta bolsa de compresión se puede plegar, ahorrando espacio y siendo portátil.
- A PRUEBA DE AGUA - Saco seco ligero con costuras selladas que mantienen seguros sus objetos de valor. Perfecto para sus viajes, fácil de transportar, se puede reducir de tamaño al comprimirla o enrollarla.
- DISEÑO SEGURO -En materiales duraderos, solido y robustos, diseñada para el uso en exteriores, waterproof. Esta cómoda mochila seca o bolsa de supervivencia cuenta con una correa para el hombro y una hebilla que la mantiene bien sellada.
- APLICACIONES - Esta mochila de almacenamiento es ideal para activitades acuaticas, ir de pesca, kayaking, navegar, excursiones, senderismo, natación, ciclismo, todo tipo de deporte acuático.
- SERVICIO AL CLIENTE 24/7. Recibirá su producto con su factura con el IVA incluido.


Muc Off C3 Ceramic Dry Lube - Lubricante cerámico para bicicleta , 120 ml
- Ideal para MTB, Road & Cyclocross- Fórmula biodegradable con base libre de derivados del petóleo ideal para condiciones secas y polvorientas; Crea una capa cerámica que protege la cadena; Prestaciones idelaes para largas distancias. Incluye luz UV para chequeo de aplicación;
- Sistema de pipeta que facilita su aplicación;
- Dimensiones: 120 ml


The North Face T92TX3 Camiseta Easy, Hombre, Blanco (Tnf White), XXL
- Camiseta clásica de manga corta con cuello redondo
- Estampado prensado en plastisol en la parte delantera y trasera
- Es de la marca The North Face


El libro conciso de la punción seca. Manual del terapeuta para las aplicaciones en los puntos gatillo miofasciales (Medicina)


Tarrago High Tech Nano Protector - Impermeabilizante Para Ropa, Textil, Cuero y Ante, 250ml
- Apto para todo tipo de materiales: Para piel, piel sintética, piel engrasada, ante, nubuck y textil.
- Repele la suciedad, sin alterar los colores originales ni las características naturales de la piel y no dificulta la transpiración.
- Producto testado y recomendado para calzado de membranas transpirables e impermeables.


Yeast (Brewing Elements): The Practical Guide to Beer Fermentation


Leisure Suit: Larry - Wet Dreams Don't Dry - Nintendo Switch
- Leisure Suit Larry vuelve en 2019: sí, has leído bien
- Explora un mundo no lineal, diseñado al detalle y ambientado en 2018 con más de 30 escenarios dibujados a mano
- Utiliza Timber, una app con un innovador sistema de ligoteo que te permitirá quedar con chicas, mejorar tu puntuación en la plataforma y, en última instancia, conquistar a Faith, la mujer de tus sueños
- Resuelve acertijos e interactúa con más de 30 personajes dibujados a mano

Imágenes de Aplica dry
Aquí puedes ver un conjunto de fotos de aplica dry para que te formes una idea y puedas escoger entre todos los tipos de colonia. Pincha con el ratón en una de las imágenes para ver la ficha íntegra del producto y su precio.