Punto pack mas cercano
Los mostradores de belleza y las tiendas on line de incontables compañías de perfumes están llenos de lo último y lo mejor, así que ¿cómo sabes cuál será tu próximo destino? Pues te lo decimos nosotros: punto pack mas cercano, punto pack paris o punto pack telefono. La mejor colonia para hombres o mujeres ha de ser esmeradamente emparejada con las situaciones y ocasiones específicas en las que se empleará. Los seductores aromas oscuros, de tabaco y madera se adaptan a los acontecimientos nocturnos, al paso que las fragancias más frescas o bien cítricas marchan mejor para el empleo diario y la oficina. Hay múltiples familias de fragancias para escoger, incluyendo las leñosas, orientales, herbales, florales, etcétera Muchos especialistas aconsejan el uso de las flores en todas las estaciones, al tiempo que las yerbas son las mejores colonias para el verano. Generalmente, las olores leñosas y orientales sirven mejor a lo largo de los meses de invierno.
Listado top ventas para Punto pack mas cercano
Aquí puedes comprar multitud de artículos como punto pack mas cercano magníficos para el cuidado de tu salud. Que sepas que para poder encontrar sinfín de opciones para poder comprar lo mejor para tu salud, te encuentras en uno de los mejores sitios web de la red.

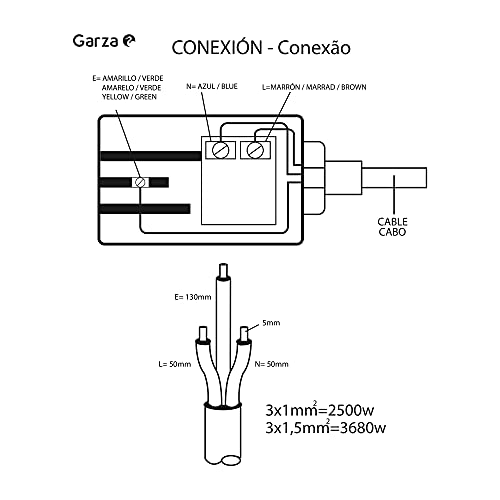
Garza regleta enchufes sin cable, blanco, 3 tomas
- Regleta enchufes multiples de 3 tomas con interruptor
- Regleta sin cable con la posibilidad de conectar el más conveniente según las necesidades
- Ladrón con protección infantil
- Color blanco
- Toma de tierra
- Máximo: 3680W 16a / 250v
- Formato de enfuche: 2 pines toma schuko
- Medidas regleta: 5.20 x 4.80 x 20.5 cm
- Para más información revisa el manual de instalación de un cable en la regleta y datos técnicos del producto


Unigear Guantes Running Correr Pantalla Táctil Guantes Primera Capa para Actividades al Aire Libre Senderismo,Corriendo,Senderismo,Viajes,Carrera,Ciclismo, Otoño e Invierno o Forro de Guantes Esquí
- Súper Cálido & Tranpirable:Este Guantes deportivos usando la tela última de fibra de terciopelo, el volumen de la tela aumenta 10% más que otras fibras similares. La función perticular de absorción de humedad permite que la tela libere rápidamente la humedad hacia el exterior del cuerpo, dejando el calor en el cuerpo para lograr la función de absorción de humedad y mantener el calor. Este guante para correr aplica un tratamiento antiestático de tejidos y un tratamiento antipilling.
- Pantalla Táctil:El pulgar y el índice de dos manos están unidos con microfibra conductora, que es fácil y sensible para controlar productos electrónicos, resistente al desgaste y puede usarse repetidamente.
- Antideslizante:Las partes de la palma y los dedos están hechas de silicona antideslizante resistente al desgaste, lo que mejora la fricción, hace que el agarre sea más seguro, evita el peligro de resbalón de los manos, garantiza la seguridad durante el uso del ciclismo y la conducción.
- Cómodo & Durable:La tela tiene elasticidad en cuatro direcciones, suave y cómoda, se adapta a la mano y es muy ligero. La parte de la unida de la palma con los dedos están diseñadas sin costuras para reducir el peoblema de agrietamiento. La parte de costura utiliza puntadas de cadena y puntadas.Lo que es flexible, puede estirarse la linea junto con la tela sin romper.
- Servicio al Cliente de Alta Calidad : Si tiene cualquier problema sobre el producto que recibe o si se producen problemas de calidad contáctenos, le responderemos y le propondremos soluciones la primera vez.

![[Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM [Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM](https://www.iesribera.es/pics/2022/03/04/nuevo-tp-link-deco-x50-3-pack-sistema-wifi-6-ai-mesh-ax3000-doble-banda-24-ghz5-ghz-cobertura-hasta-600-m2-3x-puertos-gigabit-por-unidad-ba-383887.jpg)
[Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM
- WIFI 6 CONEXIONES MÁS RÁPIDAS - El WiFi 6 acelera hasta 3000 Mbps - 2.402 Mbps a 5 GHz y 574 Mbps a 2,4 GHz. Además dispone un ancho de banda en 160MHz para conexiones inalámbricas más rápidas
- VELOCIDAD GIGABIT ETHERNET - Hay 3 puertos Gigabit 10/100/1000 Mbps por unidad para conexiones por cable
- CONECTE MÁS DISPOSITIVOS - La tecnología OFDMA y la capacidad de cuatro núcleos MU-MIMO para permitir la transmisión simultánea hasta 150 dispositivos
- UNA RED UNIFICADA MESH- Varias cajas forman una red doméstica completa que selecciona automáticamente la mejor conexión cuando se mueve por la cas
- SEGURIDAD TOTAL - Con cifrado WPA3 y TP-Link HomeCare ofrecen funciones personalizadas, como control parental, antivirus y calidad de servicio (QoS) para garantizar una experiencia online más segura.
- CONFIGURACIÓN SENCILLA - Puedes configurar todo desde la aplicación Deco que te guía paso a paso en la configuración.


Dungeons & Dragons - Player’s Handbook: Manual del Jugador (Edge Entertainment EEWCDD01)
- Todo lo que un jugador necesita para crear personajes heroicos para el juego de rol más importante del mundo
- El Manual del Jugador es el documento de referencia esencial para todo jugador de Dungeons & Dragons te sumerge en un mundo de aventura
- Explora antiguas ruinas y letales mazmorras
- Producto en castellano
- Recomendado a partir de 12 años de Edad


Brújula de Orientación (la Herramienta Básica para Supervivencia y Navegación durante Acampada, Senderismo, Excursionismo) - Aguja Magnética, con Líquido, Cojinete Azimut, con Graduaciones por Mapa
- Indicación Precisa, Fácil de Leer y Sencillo de Usar - Fácil de Girar el Bisel y Marcar la Dirección Exacta
- Pequeña y Compacta, Cápsula con Líquido, Aguja Magnética, Lupa para Leer Mapas
- Brillando en la Noche y Luminosa en la Oscuridad gracias a las Agujas y Flechas Direccionales Fósforosas
- 100% Seguro! Con Garantía del Fabricante y Entregado por Amazon
- La brújula topográfica es el instrumento indispensable en su mochila, kit de viaje o bolsillo. Si estas buscando por la herramienta precisa en que puedes confiar durante tus escaladas, expediciones o exploraciones en los bosques y montaña, entonces ¡Este es el compass perfecto para ti! Así que ¡Prepara por Aventuras Ya y Consigue la Tuya Ahora! (Inventario variable en la temporada alta)


Las casualidades no existen: Espiritualidad para escépticos


Almirón Profutura 2 Leche de Continuación en Polvo, desde los 6 Meses, 800g
- Fórmula de continuación en polvo
- Indicada a partir de los 6 meses
- Con componentes idénticos a los de la leche materna
- Favorece la absorción de ácidos grasos y calcio
- Ayuda al normal funcionamiento del sistema inmunitario gracias a las vitaminas C y D

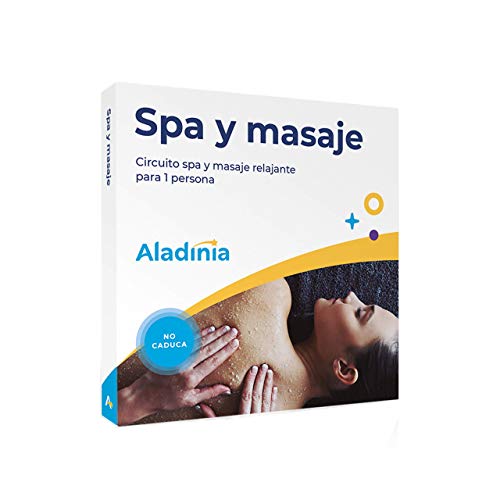
ALADINIA Spa y masaje. Paquete de experiencias para regalar. Cofre con circuito spa y masaje, ideal para hombres o mujeres. Sin caducidad, cambios gratis e ilimitados
- Pack de circuito Spa y Masaje para 1 persona a elegir entre más de 30 spas, hammam, balnearios y baños árabes en España.
- Aparecen en esta caja: Hotel Frontair Congress 4* (Barcelona), Hotel Gran Claustre 4* (Tarragona), Hotel Macià Real Alhambra 4* (Granada), Atalanta Sport Club (Valencia), Agua y Salud (Sevilla), Hammam Open Space (Málaga)
- Bonos sin caducidad. Tras un primer periodo de validez, normalmente de 12 meses, el cheque regalo seguirá estando vigente. Solo tendrás que reactivarlo. Fecha abierta: el beneficiario decide cuando disfrutarlo.
- Cambios ilimitados y sin coste. Puedes usar tu cupón como saldo para comprar cualquier experiencia de nuestra web. Más de 3.000 ideas de regalo originales para hombres, mujeres o parejas.
- Aladinia es el mayor ecommerce de experiencias de España. Fundada hace más de 10 años, ha vendido más de 500.000 experiencias, trabaja con más de 1.000 proveedores de actividades y cuenta con más de 30.000 opiniones de clientes.


Nespresso Krups Essenza Mini XN1101 - Cafetera monodosis de cápsulas Nespresso, compacta, 19 bares, apagado automático, color blanco (Pack Cápsulas bienvenida incluido)
- La cafetera de Nespresso de diseño moderno ultracompacto para la máxima comodidad, ocupando el menor espacio posible con un tamaño de 33 x 8,4 x 20,4 cm
- 2 programas de café para elegir la medida deseada: café corto o largo y también puedes personalizar las cantidades como más te guste
- Ahorro de energía: activación del modo de bajo consumo de energía al cabo de 3 minutos y función de autoapagado tras 9 minutos de inactividad
- Capacidad del contenedor de capsuladas usadas: 9 cápsulas
- Sistema Nespresso de 19 bares de presión y calentamiento rápido en sólo 25 segundos


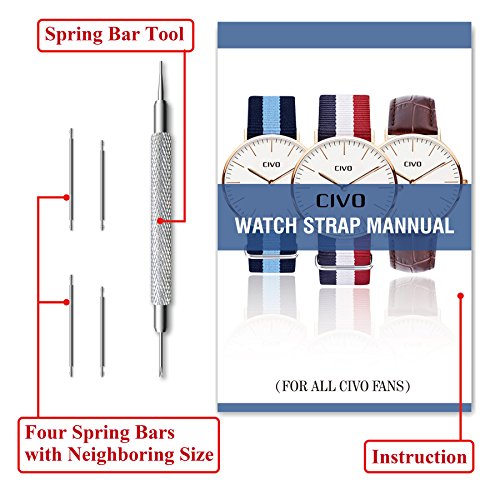
CIVO Correas de Reloj NATO Zulu Nailon Balístico Correa Reloj de 18mm 20mm 22m para Hombre Mujer
- Julio DEAL: Ahora para todos los productos de banda reloj en la tienda CIVO, comprar 2 para obtener un 10% de dinero, comprar 3 para obtener el 15% del dinero fuera, comprar 5 o más para obtener el 20% del dinero fuera! No es necesario introducir código de reclamo, el dinero se ajustará automáticamente al check-out. Incluso si usted compra varios productos diferentes de diferentes anuncios en nuestra tienda CIVO, todavía se podrá disfrutar de esta oferta!
- PERFECTO nylon balístico Y HARDWARE: Alta Calidad (más estricta) tejen 1,3 mm de espesor de nylon balístico, hardware rectangular delgada (de acero inoxidable) con pulido, cepillado, acabados PVD y oro, fabricada con costuras. Nuestras correas CIVO OTAN se destacan de otras correas de reloj regulares en el mercado debido a la calidad de la armadura superior de nylon balístico, opciones de acabado de hardware, y fabricada con costuras.
- Construcción perfecta, FÁCILES DE INSTALAR, prueba del agua y lavable: A diferencia de imitaciones utilizando pegamento barato y costura, que fomentará el crecimiento de bacterias y llegar a ser maloliente, bandas Civo son lavables a máquina y huelen mal-libre, mientras que la construcción cosido y corte láser para evitar raedura. Lo más importante, 1 alta calidad herramienta de la barra de resorte y barras de resorte de acero inoxidable de tamaño 4 vecina para cambiar la correa del reloj.
- 100% sirve para todos MUÑECAS: 11 pulgadas de largo y 3 de ancho de tamaño (18 mm, 20 mm y 22 mm,). CIVO longitud de la banda de reloj se ajusta a las muñecas de 5 a 9 pulgadas de circunferencia, que cubre la mayor parte de la población. Se puede ajustar la longitud o cambiar la forma en que lo usa de acuerdo al manual. Para seleccionar el ancho, la anchura medida de la terminal de reloj o el ancho de banda actual en el punto de conexión y luego seleccione el ancho más cercano a la medición.
- COMPRA sin preocupaciones: Cada banda de reloj CIVO viene con una garantía de 6 meses y 90 días 100% del dinero de garantía de devolución. A pesar de nuestras correas de reloj casi cubrir la totalidad de la muñeca y ver el tamaño, si usted todavía piensa que no encajaba como espera, o si tiene cualquier otra insatisfacción, envíe un correo electrónico a nuestro equipo de servicio post-venta, se te reembolsará el 100% de su dinero , ninguna pregunta hecha!


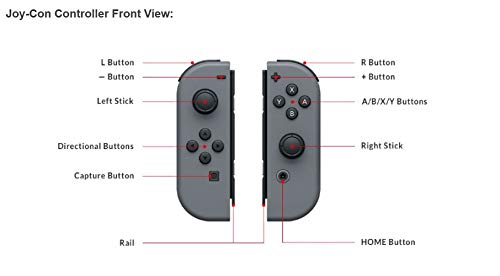
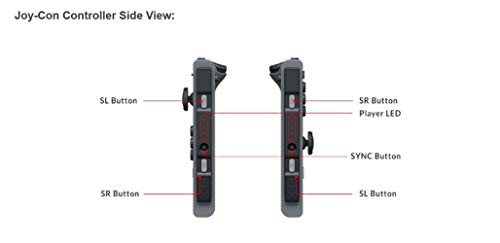
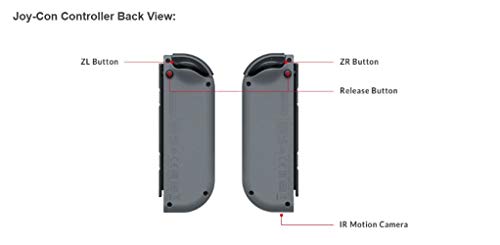
Joy-Con (set Izda/Dcha) Azul / Amarillo Neón
- Set compuesto por un mando Joy-Con azul (Izquierda), un mando Joy-Con amarillo neón (Derecha) y dos correas.
- Con los nuevos mandos Joy-Con para Nintendo Switch tendrás flexibilidad total a la hora de jugar y descubrirás nuevas formas de interactuar que transformarán por completo tus experiencias de juego.
- Su diseño incluye la sofisticada función de vibración HD, que ofrece una vibración mucho más realista que antes, y permite utilizar uno en cada mano o compartirlos con un amigo; además de poder incorporarlos al armazón para controles Joy-Con (venta por separado) que los transformará en un mando de estilo tradicional.
- Cada Joy-Con contiene sus propios botones, sensor de acelerómetro y sensor de movimiento que posibilita que puedan funcionar como un mando independiente.
- Además, los Joy-Con integran nuevas prestaciones que hacen de Nintendo Switch más interactiva. Por un lado, el Joy-Con izquierdo tiene un botón de captura para hacer capturas de pantalla durante tus partidas y compartirlas a través de las redes sociales. El Joy-Con derecho, por su parte, dispone de un punto NFC para usar figuras amiibo, así como una cámara infrarroja de movimiento que detecta la distancia, forma y movimiento de objetos cercanos en los juegos diseñados para esta tecnología.


Culpa mía (Culpables 1)


Scholl Plantillas, óptimas para zapatos de tacón alto con tecnología Gel Activ, discreción y comodidad, 2 plantillas
- La tecnología Scholl GelActiv se centra en el uso de un núcleo de gel suave y elástico que hace que incluso los tacones más vertiginosos sean tan cómodos como cualquier par de zapatillas deportivas
- Gel transparente, fino y con un diseño discreto que aumenta la comodidad en el antepie
- Para zapatos de tacón de más de 5.5 cm de alto
- El material de agarre y los pequeños relieves en la superficie de las plantillas previenen el deslizamiento incluso con sudor
- Aumenta el confort de todos y cada uno de tus zapatos durante todo el día; no comprime los dedos

Imágenes de Punto pack mas cercano
Aquí tienes una agrupación de imágenes de punto pack mas cercano para que te hagas una idea y puedas elegir entre todos los tipos de perfume. Pincha en una de las fotografías para ver la ficha completa del producto y su costo.








![[Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM [Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM](https://www.iesribera.es/pics/2022/03/04/nuevo-tp-link-deco-x50-3-pack-sistema-wifi-6-ai-mesh-ax3000-doble-banda-24-ghz5-ghz-cobertura-hasta-600-m2-3x-puertos-gigabit-por-unidad-ba-383887-2.jpg)
![[Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM [Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM](https://www.iesribera.es/pics/2022/03/04/nuevo-tp-link-deco-x50-3-pack-sistema-wifi-6-ai-mesh-ax3000-doble-banda-24-ghz5-ghz-cobertura-hasta-600-m2-3x-puertos-gigabit-por-unidad-ba-383887-3.jpg)
![[Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM [Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM](https://www.iesribera.es/pics/2022/03/04/nuevo-tp-link-deco-x50-3-pack-sistema-wifi-6-ai-mesh-ax3000-doble-banda-24-ghz5-ghz-cobertura-hasta-600-m2-3x-puertos-gigabit-por-unidad-ba-383887-4.jpg)
![[Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM [Nuevo] TP-Link Deco X50 (3-Pack)- Sistema WiFi 6 AI Mesh, AX3000 Doble Banda 2.4 GHz/5 GHz, Cobertura hasta 600 m², 3X Puertos GigabIt por Unidad, Banda 160MHz Canal, ODFMA, 1024QAM](https://www.iesribera.es/pics/2022/03/04/nuevo-tp-link-deco-x50-3-pack-sistema-wifi-6-ai-mesh-ax3000-doble-banda-24-ghz5-ghz-cobertura-hasta-600-m2-3x-puertos-gigabit-por-unidad-ba-5.jpg)