Para obtener una emulsion hace falta
Para ayudar a guiar tu búsqueda, es una buena idea meditar en las olores de acuerdo a las distintas categorías: florales, frutales, madereras o limpias, ya que la mayor parte de la gente se inclina innatamente cara una de ellas. Eso te va a ayudar a reducir las opciones, cuando menos un poco y vas a poder enfocarte en productos más atractivos para ti como para obtener una emulsion hace falta, tampones falta o bien que hace una crema revitalizante. ¿Se ha preguntado alguna vez por qué los sommeliers se empeñan en que el vino se sostenga en un ambiente seco, evitando la variación de la temperatura y sosteniendo la botella fuera de la luz solar directa? Es para preservar el equilibrio de sus componentes y, como es lógico, la misma teoría se aplica asimismo a su colonia o perfume favorito. Para asegurarse de que emite las señales olfativas adecuadas, acá hay un resumen de las mejores colonias para hombres y mujeres de todos y cada uno de los tiempos, tanto si precisa una olor fresca para el uso diario o algo dramático y audaz para esos instantes singulares.
Listado top ventas para Para obtener una emulsion hace falta
Esperamos que con este grupo de productos encuentres para obtener una emulsion hace falta al mejor precio y buena calidad para el cuidado y bienestar de tu salud. Toma conocimiento de que para encontrar multitud de opciones para obtener lo mejor para tu salud, te encuentras en uno de los mejores sitios web del mercado.

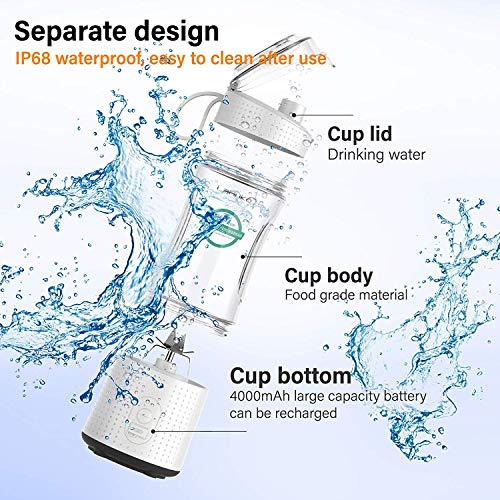
LaHuko Licuadora Portátil, Mini Batidora Personal para Batidos y Smoothies, 4000mAh batería con USB Recargable (Individuals 380ML, Blanco, para Jugo, Batido, Salsas, Comida para Bebé)
- 【Grado alimenticio y multifuncional】 La carcasa de la taza batidora portatil está hecha de PC sin BPA, grado alimenticio y ecológica, adecuada para mezclar frutas y verduras, reserva el sabor original de jugo, batido y comida para bebés . Simplemente disfrute de la retención de nutrientes frescos y de un maravilloso tiempo libre.
- 【Excelente batidora y exprimidor rápido】 Esta batidora individual actualizada está equipada con una cuchilla de acero inoxidable de seis cuchillas y tres capas con una fuerte velocidad de rotación (22000 rpm), un botón para triturar sin esfuerzo las frutas y verduras en increíbles batidos. Solo toma 45 segundos para una taza de jugo, ¡reponga su energía cuando lo desee.
- 【Jugo sobre la marcha】 La extractor zumos viene con un diseño elegante y súper ligero, solo 470g, capacidad a 380ml, ¡diseñado para una máxima portabilidad! Es lo suficientemente compacto como para guardarlo en su bolso, maletíno mochila y es una alternativa perfecta a la botella de agua. Ideal para llevarlo de viaje.
- 【Recargable y de alta capacidad】 La juicer cup está equipada con una batería recargable de 2*2000 mAh incorporada que se puede cargar fácilmente con todo tipo de dispositivos USB, como un banco de energía, una computadora portátil, etc. 18 tazas de jugo, mucho más conveniente que el exprimidor tradicional.
- 【Fácil limpieza y garantía de 12 meses】 La exprimidor zumos es resistente al agua IP68 y se puede enjuagar directamente, mientras que es mucho más molesto limpiar el exprimidor eléctrico tradicional. Ofrecemos una garantía de 12 meses y un servicio al cliente profesional. Su experiencia con el producto significa mucho para nosotros. Si tiene alguna pregunta sobre la licuadora, contáctenos cuando lo desee. Lo resolveremos tan pronto como podamos.


Cecotec Robot de Cocina Multifunción Mambo 10070. Cuchara MamboMix, 30 Funciones, Báscula incorporada, Jarra de Acero INOX de 3,3 L, Apta para lavavajillas
- Robot de cocina multifunción con 30 funciones: trocea, pica, licua, tritura, sofríe, muele, pulveriza, ralla, recalienta, bate, yogurtera, monta, emulsiona, mezcla, cocina, remueve, cocina al vapor, escalfa, confita, amasa, cocina a baja temperatura, hierve, mantiene caliente, fermenta, SlowMambo, cocina con precisión grado a grado, cocina al baño maría, cocción lenta, velocidad cero y dispone de función turbo.
- Jarra de acero inoxidable de alta calidad apta para una limpieza rápida y fácil en el lavavajillas. Su velocidad cero permite cocer y sofreír sin necesidad de poner velocidad, como si de una cazuela o una sartén se tratase. Y, además, con la ventaja de cocinar sin tapa. La innovadora función Sofrito a una temperatura superior cuando desees utilizarla para dorar los alimentos, se consigue con la mayor temperatura y la máxima potencia.
- Exclusiva cuchara MamboMix para amasar. Al no cortar la masa logra que sean más homogéneas y tengan un mayor volumen. La jarra cuenta con una gran capacidad máxima de hasta 3,3 litros para que no se tengan que repetir las elaboraciones cuando hay invitados en casa. Cestillo de hervir para poder preparar hasta 4 elaboraciones al mismo tiempo.
- Disfruta de la App Mambo para Smartphone con recetas ilimitadas guiadas paso a paso, modos predefinidos para facilitar su uso y sistema manual DIY. Incorpora báscula para pesar con gran precisión los alimentos depositados en la jarra con el fin de trabajar con cantidades exactas y obtener excelentes resultados.
- Incluye un completo recetario y acceso a la comunidad social interactiva y a todas las recetas nuevas semanales de Cecotec.


Goma Xantana 200g Sin Gluten, Vegano. Para espesar
- 🍮 Espesante tanto en frío como en caliente. Espa batidos, sopas, salsas.. Aporta estabilidad a cremas, merengues y nata montada
- 👨🍳 Básico en pan y reposteria sin gluten. Keto. Combinalo con nuestro psyllium para obtener óptimos resultados
- ALERGENOS: Sin gluten, leche, huevo, frutos, secos ni soja. Vegano. 100% vegetal


Lorann Oils Sabor Natural y Artificial Bakery Emulsions 118 ml, Tarta de Terciopelo Rojo, Multicolor
- Adecuados para decoración del hogar.
- Adecuados para proyectos artísticos y manualidades.
- Fácil de usar y guardar.


Moulinex Multimoulinette Compact DJ300110 Picadora, 0.25 l de Capacidad, Sistema de Seguridad Integrado, 270 W, Plastique, Blanco
- Bol graduado con capacidad útil de 0.6 l
- 270 W de potencia
- Funciona por presión, sistema 1,2,3
- Sistema de seguridad permanente, la picadora solo funciona con la tapa encajada
- Bol, tapa interior y cuchilla aptas para el lavavajillas
- Componentes incluidos: tazón extraible
- Bol graduado con capacidad útil de 0.25 l
- 270 W de potencia
- Funciona por presión, sistema 1,2,3
- Sistema de seguridad permanente, la picadora solo funciona con la tapa encajada
- Bol, tapa interior y cuchilla aptas para el lavavajillas


Naissance Manteca de Karité BIO n. º 306 – 500g – Pura, natural, certificada ecológicamente, sin refinar, elaborada de forma artesanal y vegana – Obtenida de forma ética y sostenible en Ghana.
- Manteca de karité 100 % pura, sin refinar, certificada ecológicamente y proviene de Ghana. INCI: Butyrospermum parkii.
- Manteca de karité 100 % pura, sin refinar, certificada ecológicamente y proviene de Ghana. INCI: Butyrospermum parkii.
- Contiene altos niveles de ácidos grasos insaturados y antioxidantes naturales. Puede ayudar a mantener la piel hidratada y actuar como barrera protectora contra los factores externos. Se suele usar en mantecas corporales, cremas, lociones, bálsamos labiales y productos para el cabello. Más información sobre usos en la descripción.
- Su aroma es natural, característico e intenso, su color es amarillo claro o crema y su textura es sólida. Los bloques de manteca se derriten a baja temperatura para su envasado.
- Obtenemos nuestra manteca de karité de una cooperativa de mujeres ubicada en Wa, al norte de Ghana. Esta cooperativa de unas 600 mujeres apoya a su comunidad para conseguir un futuro mejor a través de la producción de manteca de karité BIO.
- Vegano 🌻 y no probado en animales🐇 No OGM.


Detox Depurativo Higado y Colon Diurético Natural | Complejo Bio Alcachofa Rábano Negro Cúrcuma Orgánica | Drenante Desintoxicante Digestión Limpieza Intestinal | Vegano 90 Cápsulas Hecho en Francia
- DIURETICO NATURAL : Suplemento Natural Para El Hígado, Potente Detox Cleanser combinación de cuatro Hierbas Naturales, Alcachofa Rábano Negro y Cúrcuma. Suplementos Naturales desintoxica tu organismo y mejora tu digestión. Perder el exceso de líquido y las retenciones de agua son uno de los grandes pasos hacia el adelgazamiento. Favorece una buena digestión, mejora el tránsito intestinal y de colon.
- DESINTOXICAR CUERPO : Ayuda a tu dieta quemar grasa para eliminar, depurar y drenar el organismo. Ayuda a reducir las calorías ingeridas de carbohidratos, azucares y grasas. Combate la acumulación de liquidos. Ayuda a disminuir el almacenamiento de la grasa acumulada en el cuerpo. Es un complemento alimenticio, que mediante su uso eliminaremos líquidos, mejoraremos nuestra piel y nuestro metabolismo. Contribuye a la pérdida de peso y elimina las toxinas y los desechos del cuerpo
- DEPURATIVO HIGADO : Este complemento alimenticio Detox Natural con hierbas naturales ayuda al control del colesterol en el hígado, ayuda a bajar de peso y también facilita el adecuado metabolismo de las grasas. Activa el drenaje hepático y alivia los trastornos digestivos. Contribuye a la buena digestión favoreciendo la eliminación de los gases evitando así que causen molestias e hinchazón abdominal. Actua a nivel intestinal facilitando la emulsión de las grasas y regulando su absorción.
- ELIMINA TOXINAS : La Alcachofa mejora el funcionamiento de los riñones, haciendo que todo el proceso de orinar sea mucho más rápido y fluido, evitando la retención de líquidos. El Rábano Negro favorece al drenaje tanto del hígado como de la vesícula biliar, por lo que ayuda a la eliminación de toxinas y residuos. Ayuda a mejorar la digestión y la desintoxicación del cuerpo. La Curcuma tiene propiedades antioxidantes, antiinflamatorias y depurativas. Prode origen vegetal
- PRODUCTO NATURAL : Cápsulas de origen vegetal. Todos los ingredientes provienen de la agricultura biologica. Podrucido y Fabricado en Francia. Programa completo para un mes. Una fórmula específica para reducir la grasa de las piernas, drena el exceso de liquidos. - **ATENCIÓN : No se deje engañar con productos similares de bajo precio, que pueden causarle daños irreparables al organismo por ser de dudosa procedencia.**


Crema conductora Facial Lifting bellaline


Moulinex Masterchef Gourmet QA530D - Robot Amasador 1100 W, Bol de Acero Inoxidable 4.6 L, para batir, emulsionar y amasar, 8 velocidades, Kit de pastelería + accesorios silicona y libro de recetas
- El robot de cocina adecuado para repostería con 1100 W para adaptarse a tu cocina; gracias a sus variados accesorios pero si en algo sobresale es en su tratamiento de los postres y repostería
- Su potencia de 1100 W cuenta con 8 tipos de velocidades diferentes + pulse; aplica su tecnología Flex Whisk a las mezclas, por lo que se consiguen mezclas de gran calidad, con los ingredientes unidos
- Tecnología patentada Flex Whisk, para montar claras a la perfección; incluye un kit para masas con accesorios: varillas, varillas de amasar para repostería y gancho de amasar para masas densas
- Viene con 3 accesorios para ayudarte a preparar postres; la combinación de nuestros accesorios: varillas Flex Whisk, bol Flex Bowl y el accesorio Delica'tool, te permitirán ahorrar tiempo y esfuerzo
- Capacidad del bol de acero inoxidable de 4.6 L, y tapa antisalpicaduras para mayor seguridad; incluye un accesorio para insertar otras preparaciones así como un libro de recetas
- El movimiento planetario del accesorio y el cabezal para masas permiten llegar a todos los rincones del bol, obteniendo un resultado suave y homogéneo
- Gracias a su diseño especial con tres niveles de varillas alargadas, Flex Whisk llega fácilmente al fondo del bol para montar los ingredientes y ofrece un resultado rápido, ligero y esponjoso


Scitec Nutrition 100% Whey Protein Professional Chocolate 2350 g
- Mezcla de concentrado de suero de leche y aislado
- Reforzado con enzimas digestivas y aminoácidos
- Número de modelo del producto: 0728633109661
- facil de usar


Levaka Aditivo de Pintura de Purpurina Plateada Holográfica 150 gramos - 2x Almohadillas de pulido - Mezclar con Pintura de Emulsión para Acabado Luminoso - Pintura Paredes Interior Exterior
- ¡CUALQUIERA PUEDE HACERLO! - ¡Sus paredes brillarán enseguida! Simplemente abra una bolsa del aditivo de pintura pared de alto brillo Levaka y agréguela a 1.5 l de pintura - Remueva durante unos 5 min y comience a pintar - Mezcle su proporción preferida ¡pero agregar más purpurina pared hará que sus paredes brillen aún más! - Recomendamos pintar primero una pequeña muestra para ver los efectos y proceder en consecuencia - Ideal para pinturas de brillo suave satinado mate o de emulsión sedosa
- NO TÓXICO Y SEGURO PARA NIÑOS - Los cristales de la purpurina para pintura pared cumplen con normas de la UE y son 100% no tóxicos y seguros para niños - Puede estar tranquilo somos el mayor fabricante de purpurina del UK - ¡Estas escamas brillantes son resistentes a las temperaturas e impermeables! - Use este brillo holográfico con sus colores de pinturas favoritos en la sala de estar cocina o baño - ¡Incluso puede aplicarla en el techo de la habitación de sus hijos para un efecto estrellas!
- INCLUYE 2X ALMOHADILLAS DE PULIDO DE LEVAKA - Una vez que su nuevo proyecto de brillo de pared se haya secado puede aumentar el efecto de brillo simplemente puliendo el área con las almohadillas incluidas - ¡Este proceso libera millones de cristales de brillo al adelgazar la capa exterior de pintura creando aún más brillo! - ¿Todavía desea MÁS destellos? - ¡Simplemente añada más brillo a la pintura o cambie la bombilla de la habitación a un blanco frío para un efecto chispeante único!
- CRISTAL DE PURPURINA DE TECNOLOGÍA AVANZADA - Las nuevas y mejoradas microplacas de cristal de Levaka incorporan avances en la reflexión de la luz que hacen de este aditivo para pintura el mejor del mercado - Úselo como reemplazo del papel de pared con brillo para obtener aún más efecto deslumbrante - ¡Este aditivo de pintura con brillo brinda un divertido toque de decoración interior para niños y adultos! - Use el aditivo de pintura de pared en interiores o exteriores ya que es impermeable
- COMPATIBILIDAD CON LA PINTURA - ¡Planee un brillante fin de semana pintando con los niños! - Agregue los aditivos de pintura no tóxicos a la pintura y remueva - Funciona mejor con pintura de emulsión mate o satinada pero también se puede usar con pinturas de emulsión con brillo suave - Cuando la pintura se haya secado use las almohadillas de pulido incluidas para aumentar el efecto brillo - Añada una capa de esmalte transparente para alargar la vida útil y ¡hacerlo realmente POP!


Biotherm Autobronzant Gel Visage Autobronceador - 50 ml
- Tipo de producto: Autobronceador
- Marca: Biotherm
- Género: Unisex Adulto

Bella Aurora Crema Anti-Manchas Facial para Manchas Oscuras de Origen Hormonal | Tratamiento despigmentante Cara, 30 ml
- Tratamiento antimanchas intensivo que reduce y elimina las manchas existentes y previene la aparición de nuevas de origen hormonal, con una combinación de activos que incorpora la exclusiva tecnología despigmentante B-CORE 221TM.
- B-CORE 221TM es un sistema de encapsulación y liberación dirigida. Actúa directamente sobre las células productoras de melanina dónde libera íntegramente el activo encapsulado, obteniendo así una mayor eficacia.
- ¿A quién se lo recomendamos? Pieles preocupadas por las manchas de origen hormonal.
- ¿Cómo son las manchas de origen hormonal? Manchas oscuras difusas e irregulares. Suelen presentarse a ambos lados del rostro, de forma simétrica, en zonas expuestas al sol (frente, barbilla, nariz, mejillas o labio superior). La causa de su aparición es la exposición solar sumada a factores hormonales, estrés, reacción alérgica o uso/consumo de medicamentos.
- Aplicar una pequeña cantidad sobre rostro, cuello y escote con la piel limpia, realizando un suave masaje hasta su completa absorción. Tratamiento mínimo de 8 semanas.

Imágenes de Para obtener una emulsion hace falta
Puedes ver aquí un montón de fotografías de para obtener una emulsion hace falta para que te formes una idea y puedas elegir entre todos los modelos de colonia. Pincha con el ratón en en una de las fotografías para ver la ficha completa del artículo y su coste.