Top one horario
Si tienes un presupuesto limitado y deseas encontrar un nuevo aroma propio, puedes estar sosegado sabiendo que estos perfumes asequibles no te vaciarán la cartera. Sigue leyendo y descubre productos como top one horario, horario 212 nuevo o bien horario magic internacional y prepárate a fin de que lleguen los cumplidos por tu buena presencia!. Localizar una olor consiste en familiarizarse con las notas que le gustan, las que le charlan, y elegir las fragancias en consecuencia. Adquirir un perfume por Internet puede ser difícil, pero con tantas marcas que evocan de forma deliberada determinados lugares del planeta o bien que revelan nombres que insinúan la inspiración de una olor, puedes hacerte una buena idea de lo que hay en el frasco. Cambiamos nuestra colonia casi tanto como cambiamos nuestro vestuario. Quieres asegurarte de que tu olor deje una marca en todos y cada uno de los que te rodean. Sin ser demasiado apabullante. La colonia ha avanzado mucho a lo largo de los años y hay tantas opciones basadas en tus olores favoritos, tu personalidad, la época del año e incluso la hora del día en que piensas utilizarla.
Listado top ventas para Top one horario
Te facilitamos nuestro listado de productos dónde encontrarás top one horario que tengan las necesidades de tu bienestar. Encuentra numerosas referencias de diferentes modelos con buena calidad y con predio competitivo para todo lo que necesites para tu salud.

Google Wifi - Enrutador de malla, paquete, juego de 3, para una conexión confiable, cobertura de hasta 85 m² cuadrados por punto
- Cobertura óptima en todo el hogar. Los puntos de acceso Google El wifi funciona en perfecta sinergia para proporcionarle una conexión Wi-Fi rápida y confiable en todas las habitaciones de su hogar1. Transmisión de alto rendimiento Google Wifi adapta automáticamente su funcionamiento para ofrecerle siempre un rendimiento óptimo en su red. Ve de una habitación a otra durante una videollamada sin experimentar ninguna interrupción de la señal1
- Más tranquilidad para los padres. Configura horarios de permiso de los padres para administrar el tiempo de uso o evitar el acceso a ciertos tipos de contenido para adultos, y pausa el Wi-Fi en ciertos dispositivos cuando lo desees. Una red perfectamente segura. Gracias a las actualizaciones automáticas, su red siempre está perfectamente protegida y tiene las funciones más recientes
- Una configuración rápida y sencilla. Solo te llevará unos minutos crear tu red en la aplicación Google Casa y conéctate a Internet, independientemente de tus habilidades informáticas2. Una sola aplicación para controlar toda su red. Google Wifi te permite priorizar dispositivos específicos, comprobar la velocidad de tu red3, configurar una red para invitados y mucho más, todo ello fácilmente a través de la aplicación Google Inicio 4
- Diseñado para tu hogar, diseñado para el planeta. Google El wifi está diseñado respetando el medio ambiente: el 49% del peso total de las piezas de plástico proviene de materiales reciclados


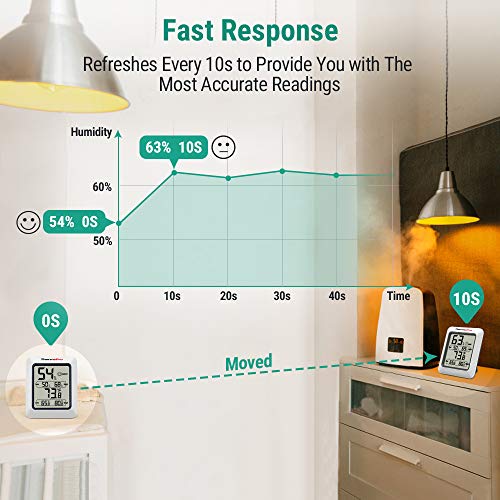
ThermoPro TP50 Termómetro Higrometro Digital para Interior Termohigrómetro Medidor Profesional para Medición de Temperatura y Humedad del Casa Ambiente
- Indicador de confort térmico: El medidor de humedad con ícono de nivel de humedad indica la condición del airea – SECO/CONFORTABLE/HUMEDO, y este sensor de humedad te permite estar siempre al tanto de los cambios en tu hogar con solo un vistazo
- Registros máximos y mínimos: El termómetro higrómetro digital preciso muestra las más altas y más bajas temperaturas y niveles de humedad; el termómetro para interiores es muy preciso, ±1°C y ±2~3% RH (humedad relativa), lo que lo hace ideal para medir lecturas fluctuantes, como en un invernadero
- Hogar y ambiente más sanos: El termohigrómetro con monitor de temperatura y humedad asegura que el control adecuado de la humedad en el interior ofrezca beneficios importantes para la piel, protección contra los alergenos y otros beneficios para la salud; También se puede utilizar como termómetro para refrigerador, congelador, reptiles, suelo, higrómetro humidor, higrómetro cigarros y más
- Diseño Inteligente: El termómetro habitación para interiores cuenta con un soporte de mesa para colocar el monitor de temperatura en su mostrador o usar el respaldo magnético para conectarlo a un refrigerador; Selector ° F / ° C; Alimentado por 1 x pila AAA (incluida)
- Registros altos y bajos: El termómetro digital higrómetro preciso muestra la temperatura y la humedad altas y bajas, siempre prepárese para los cambios del medio ambiente


Usmart Mini Enchufe Inteligente Wifi, Enchufe Alexa programable WIFI Control Remoto por APP, Smart Plug Funcionar con Monitor de Energía/Temporización, Compatible con Alexa/Google Home, 2 Packs
- 【Diseño Súpermini 】: Este enchufe inteligente alexa tiene un tamaño más pequeño del mundo y tiene un interruptor independiente, puede ahorra bien espacio. Ganó el premio de diseño Red Dot de Alemania y tiene certificación CE. Una enchufe programable mini y seguro con protección contra rayos de circuitos, sobrecorriente, protección de seguridad contra sobrecargas.
- 【Control Remoto/Voz】:Funciona con Alexa / Google Home: administre directamente sus dispositivos a través del control por voz. Mini smart plug también es compatible con el sistema telefónico (Android 4.4. Arriba / iOS 8 arriba); Y controlar de forma remota cualquier dispositivo conectado al enchufe wifi en su hogar a través de la aplicación móvil. No Requiere Hub, solo es compatible con la red Wi-Fi de 2.4GHz.
- 【Programa y Temporizador】: Al establecer horario para el enchufe temporizador de su hogar, puede encender la olla arrocera en la aplicación para cocinar con anticipación, para que pueda comer en casa después del trabajo. Establezca el tiempo para encender / apagar automáticamente cualquier dispositivo electrónico del hogar. Tenga en cuenta que la carga máxima es 16A, 2500w.
- 【Monitorización de Energía】: Cuando usa este enchufe inteligente wifi, la aplicación móvil puede monitorear la cantidad de energía utilizada, para que pueda conocer muy bien el uso de energía de los electrodomésticos conectados en su hogar y ahorrar energía.
- 【Nota】: Asegúrese de tener WiFi 2.4G antes de comprar, este producto no es compatible con la red wifi 5G. Acompaña instrucciones en varios idiomas, entre ellos, el español.


Lista de verificación del horario de hoy Be Gay Done Orgullo LGBT divertido Camiseta
- You're the gay one in the family or to come out sutil queer of the closet to your relative proud out homo
- Un adorable y adorable disfraz de arcoíris para las queers y las reinas proud de las fiestas
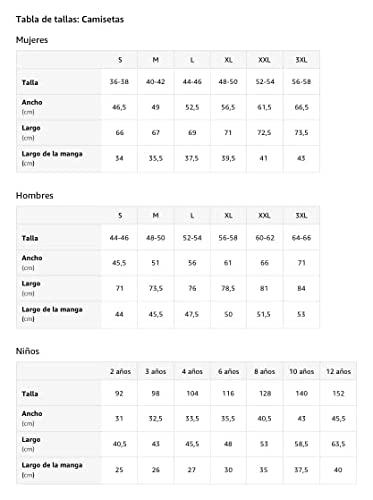
- Ligero, Encaje clasico, Manga de doble puntada y bastilla baja


ASTRO Gaming A10 Auriculares alámbricos, ligeros y resistentes, ASTRO Audio, clavija de 3.5mm, para Xbox Series X y S, Xbox One, PS5, PS4, Nintendo Switch, PC, Mac, móvil - Negro/Verde
- Construcción duradera: Para uso prolongado, de construcción ligera y robusta y materiales de calidad para un ajuste cómodo; con almohadillas de tela y cuero sintético para el rendimiento acústico
- Audio ASTRO: Cascos creados con desarrolladores, streamers y gamers, para ofrecer un audio con un espectro de frecuencia neutro, suave y ampliado y así lograr un sonido detallado y real
- Confort de larga duración: Diseñados para sesiones de juego maratonianas, los cascos para gaming A10 también se adaptan cómodamente a todos los auriculares de RV
- Flip-to-mute: El micrófono unidireccional con función flip-to-mute te permite comunicarte con tus compañeros; el ajuste de volumen proporciona control para estar a cargo de tu audio
- Compatibilidad entre plataformas: Experimenta ASTRO Audio para todo tipo de videojuegos, incluyendo consolas, PC, Mac y móvil
- Compatible con Xbox Series X y S usando el puerto de 3.5mm en el controlador Xbox
- Compatible con PlayStation 5 usando el puerto de 3.5mm en el controlador PlayStation


TP-Link TAPO P100 - Mini Enchufe Inteligente Wi-Fi, óptimo para programar el encendido/apagado y ahorrar energía, no necesita HUB, compatible con Alexa y Google Home
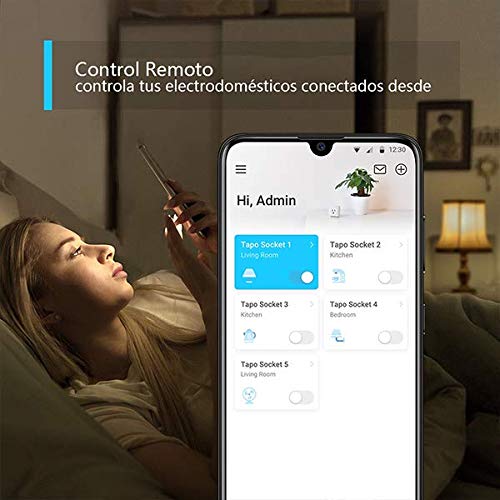
- Control remoto: enciende y apaga instantáneamente los dispositivos conectados donde sea que estés a través de la aplicación tapo
- Programación: preestablezca una programación para administrar dispositivos automáticamente
- Temporizador: crea listas de temporizadores de cuenta regresiva para los dispositivos electrónicos conectados
- Control de voz: administre su socket inteligente con comandos de voz a través de alexa o el asistente de google
- Modo ausente: enciende y apaga automáticamente los dispositivos en diferentes momentos para dar la apariencia de que alguien está en casa
- Diseño compacto: tamaño pequeño para evitar el bloqueo de tomas adyacente; (solo para toma hembra tipo C (o tomas)
- Fácil configuración y uso: no se requiere concentrador, configúrelo rápidamente y adminístrelo fácilmente a través de la aplicación


WJCRYPD Kimono japonés Mujeres Cardigan Femenino Japonés Japón Camisa de Estilo Dragon Ropa Horari de Mujer Top Kimono japonés (Color : 1, Size : One Size)
- Diferentes bellezas: la túnica larga puede mostrar sus diferentes belleza en colores elegantes con patrón de dragón
- Material de algodón avanzado, amigable para la piel, suave, transpirable, cómodo para usar.
- Textura suave y artesanía fina y colores vivos. Adecuado para desgaste diario, informal y de fiesta.
- Tu arma secreta para viajar y salir a la playa al sol, buena combinación con tu traje de baño.
- Suave y cómodo al tacto. No solo le dan la mirada más atractiva en la playa, sino que también puede proteger su piel de la quemadura solar UV.


chushi Mujeres Cardigan Femenino Japonés Japón Camisa de Estilo Dragon Ropa Horari de Mujer Top (Color : 1, Size : One Size)
- Material de algodón avanzado, amigable para la piel, suave, transpirable, cómodo para usar.
- Textura suave y artesanía fina y colores vivos. Adecuado para desgaste diario, informal y de fiesta.
- Tu arma secreta para viajar y salir a la playa al sol, buena combinación con tu traje de baño.
- Suave y cómodo al tacto. No solo le dan la mirada más atractiva en la playa, sino que también puede proteger su piel de la quemadura solar UV.
- Relájese y comodidad: suave y liso, de lujo y sedoso al tacto.Te sientes cómodo, relajado y relajado.


Casio Reloj de Pulsera AE-1000W-1BVEF
- Incluye luz LED, cronómetro, temporizadores, 5 alarmas diarias y calendario automático
- Tiene función de hora universal e indicación de hora de 12/24 horas
- Caja y correa de resina sintética, un material flexible y resistente
- La duración de la batería es de 10 años
- Resistente al agua hasta 10 bar / 100 metros


Nest Learning termostat - 3ª generación, T3010GB
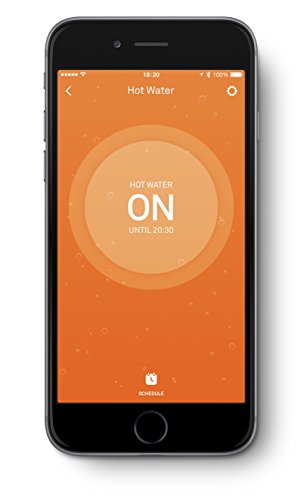
- Puede controlar el tanque y ajustar el horario de agua caliente desde móvil
- Puede cambiar la temperatura, ver historia de la energía y obtener una alerta si el hogar recibe demasiado frío
- Se adapta automáticamente para leer y establecer la temperatura correcta
- Es compatible con casi todos los sistemas de calefacción central


Nixon Reloj Unisex de Digital con Correa en Acero Inoxidable Chapado A158-502-00
- Mecanismo: digital de 4 funciones con calendario, doble huso horario, alarma, temporizador de cuenta atrás y luz
- Caja: acero inoxidable de 43 x 38,50 mm, 30 M , 3 ATM, pulsadores de poliuretano y cristal mineral endurecido
- Esfera: pantalla LCD en negativo
- Correa: acero inoxidable 12,70 mm, cierre de bloqueo deslizable y ajustable


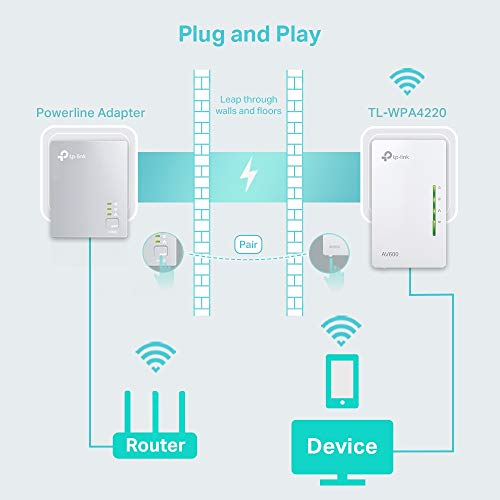
TP-Link TL-WPA4220 AV600 300Mbps - Extensor de Comunicación por Línea Eléctrica (WiF, PLC con WiFi, Extensor, Repetidores de Red, Amplificador y Cobertura Internet, 2 Puertos), 1 pieza
- Extienda la red cableada e inalámbrica a cualquier habitación utilizando el sistema eléctrico existente de su hogar
- Extensión One Range Super Range: el botón de clonación de Wi-Fi simplifica su configuración de Wi-Fi y ayuda a construir una red doméstica unificada sin problemas
- El estándar HomePlug AV proporciona velocidades de transferencia de datos a través de un cableado eléctrico doméstico, ideal para transmisión de video HD o 3D sin demoras y juegos en línea
- Extienda las conexiones inalámbricas de 300 Mbps a áreas de su hogar y oficina que antes eran difíciles de alcanzar
- Requisitos del sistema: Windows 2000 / XP / 2003 / Vista, Windows 7/8, Mac, Linux


Nueva York 9 (Guías de Ciudad Lonely Planet)


Revlon UniqONE, Tratamiento en Spray para Cabello - 150 ml
- Brillo y control del encrespado
- Facilita el peinado y el uso de la plancha
- Repara el cabello seco y dañado
- Efecto desenredante

Imágenes de Top one horario
Te mostramos aquí una galería de imágenes de top one horario para que te hagas una idea y puedas escoger entre todos los tipos de perfume. Pincha en en una de las fotografías para ver la ficha íntegra del artículo y su valor.